Слайд 1Список литературы
по дисциплине «Сложные сигналы в радиотехнических системах»
Варакин Д.Е.
Теория сложных сигналов. – М.: Советское радио, 1970. – 376
с.
Варакин Д.Е. Системы связи с шумоподобными сигналами.– М.: Радио и связь, 1985.– 384 с.
Кук Ч., Бернфельд М. Радиолокационные сигналы.– М.: Сов. радио, 1971.– 368 с.
Вакман Д.Е. Сложные сигналы и принцип неопределенности в радиолокации М.: Советское радио, 1965. – 304 с.
Дополнительная литература
Вакман Д.Е., Седлецкий Р.М. Вопросы синтеза радиолокационных сигналов. – М.: Сов. радио, 1973.– 312 с.
Свистов В.М. Радиолокационные сигналы и их обработка.– М.: Сов. радио, 1977.– 448 с.
Радиотехнические системы / под ред. Ю. М. Казаринова. — М.: Высшая школа, 1990.– 496 с.
Лёзин Ю.С. Введение в теорию и технику радиотехнических систем.– М.: Радио и связь, 1986. – 280 с.
Ширман Я.Д. Теоретические основы радиолокации.– М.:Сов. радио, 1970.– 560 с.
ГЛОНАСС. Принципы построения и функционирования/под ред. А.И. Перова, В.Н. Харисова. – М.: Радиотехника, 2010. – 800 с.
Прокис Дж. Цифровая связь / пер. с англ., под ред. Д.Д. Кловского. – М.: Радио и связь. 2000. – 800 с.

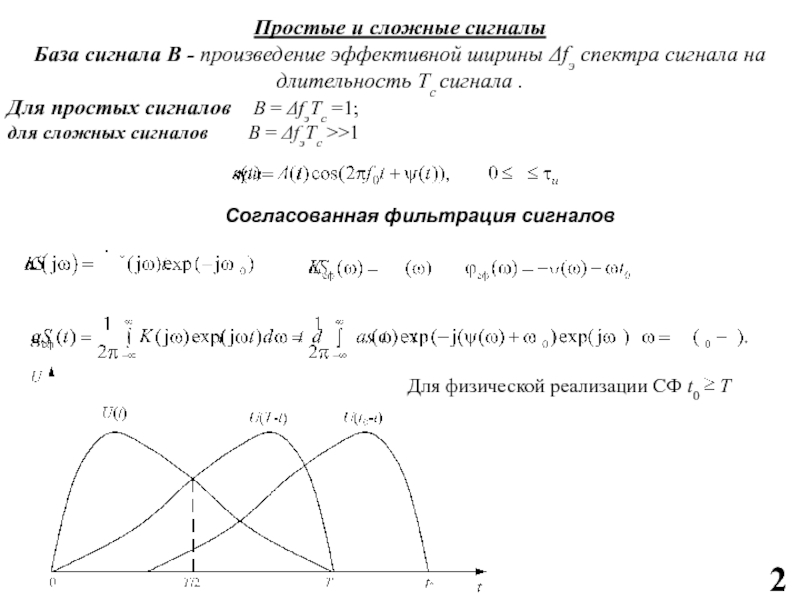
Слайд 2Простые и сложные сигналы
База сигнала B - произведение эффективной ширины
Δfэ спектра сигнала на длительность Tc сигнала .
Для простых сигналов
B = ΔfэTc =1;
для сложных сигналов B = ΔfэTc >>1
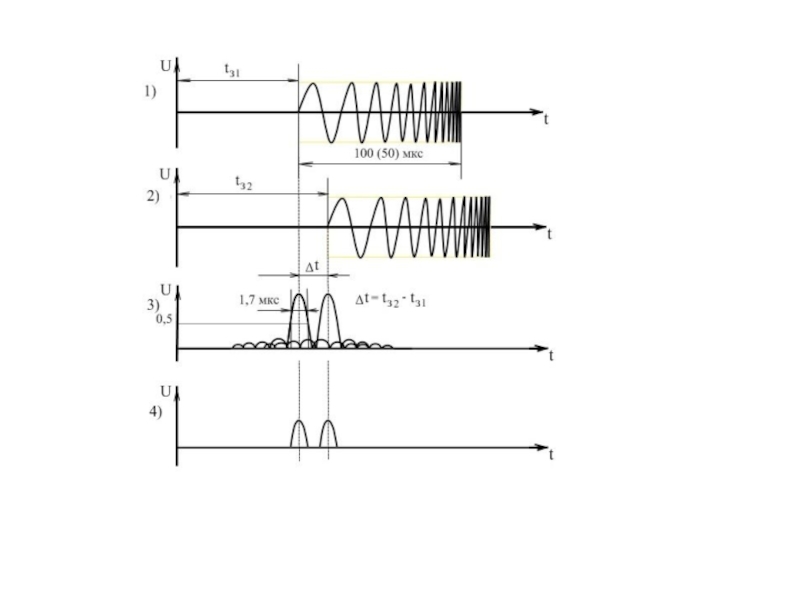
Согласованная фильтрация сигналов
Для физической реализации СФ t0 T
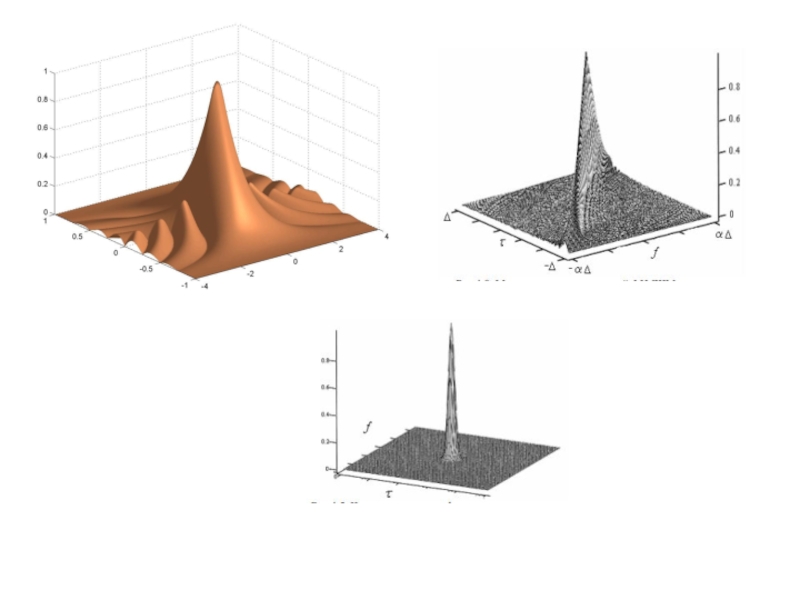
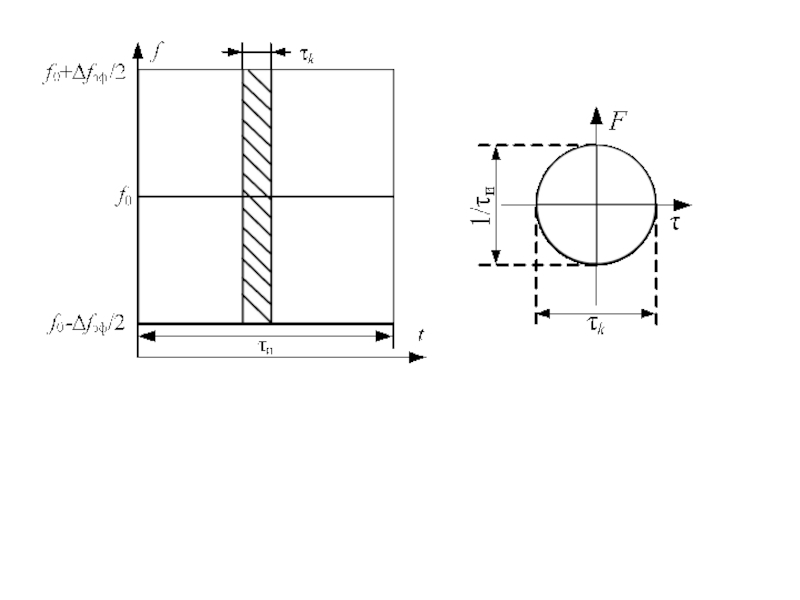
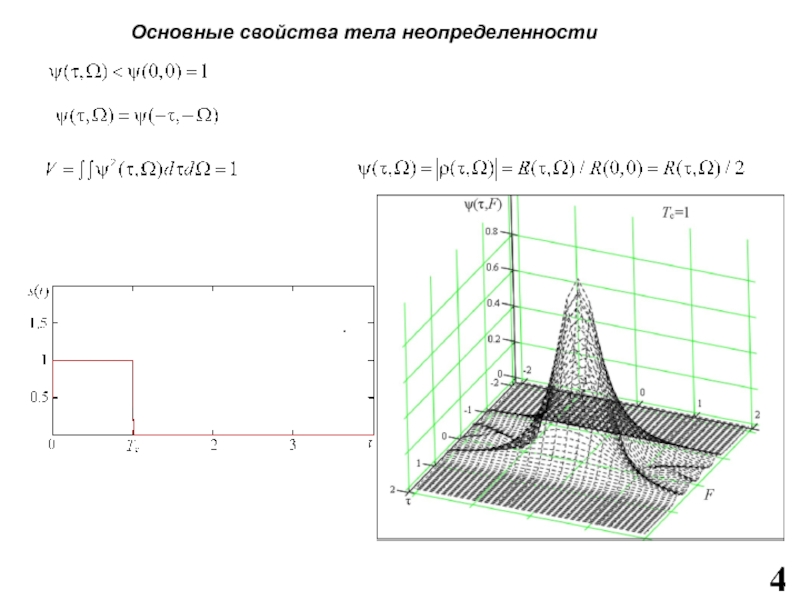
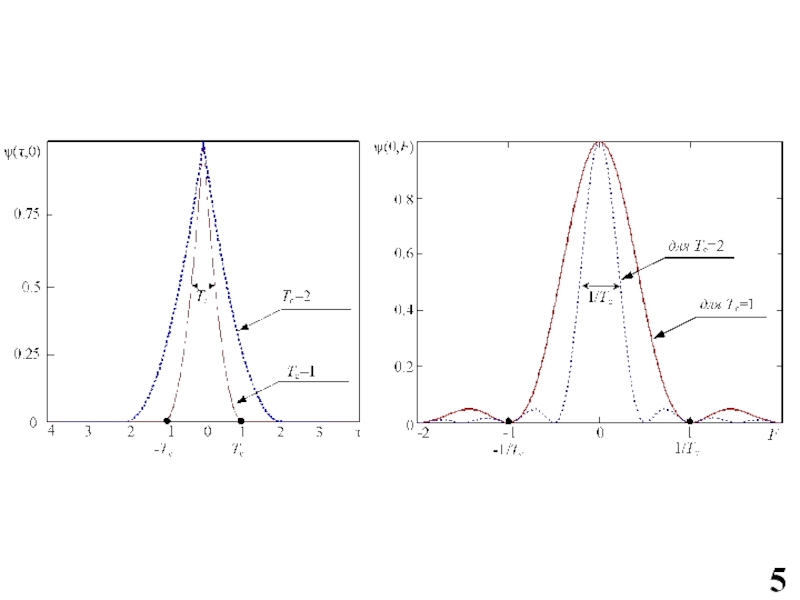
Слайд 3Функция неопределенности и ее основные свойства.
Тело неопределенности. Диаграмма неопределенности
s(t) = Um0(t) exp (iω0t+iφt) =
exp(iω0t)
Основные свойства функции неопределенности
Слайд 4Основные свойства тела неопределенности
.
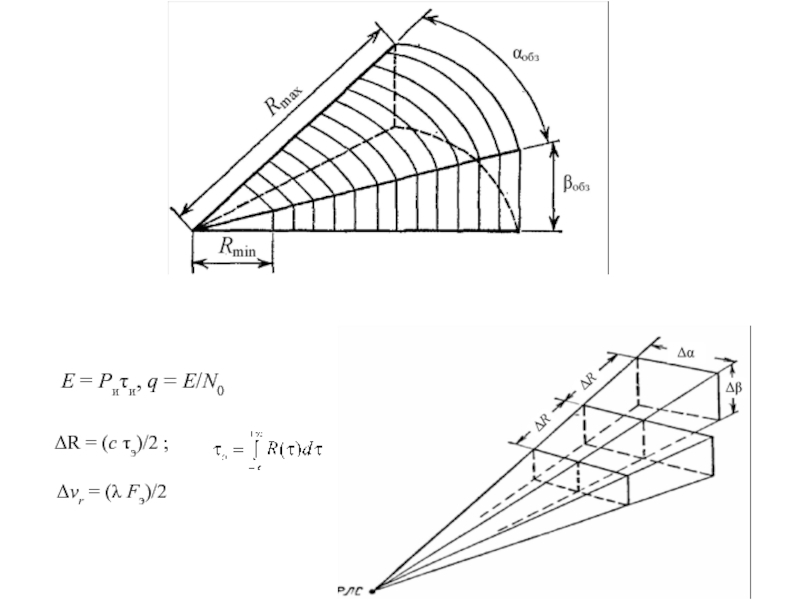
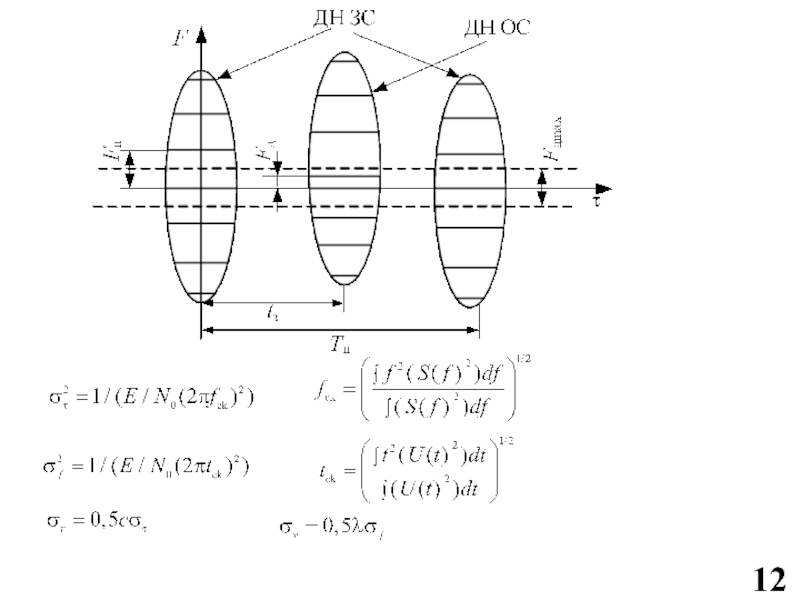
Слайд 7E = Pиτи, q = E/N0
ΔR = (с τэ)/2 ;
Δvr = (λ
Fэ)/2
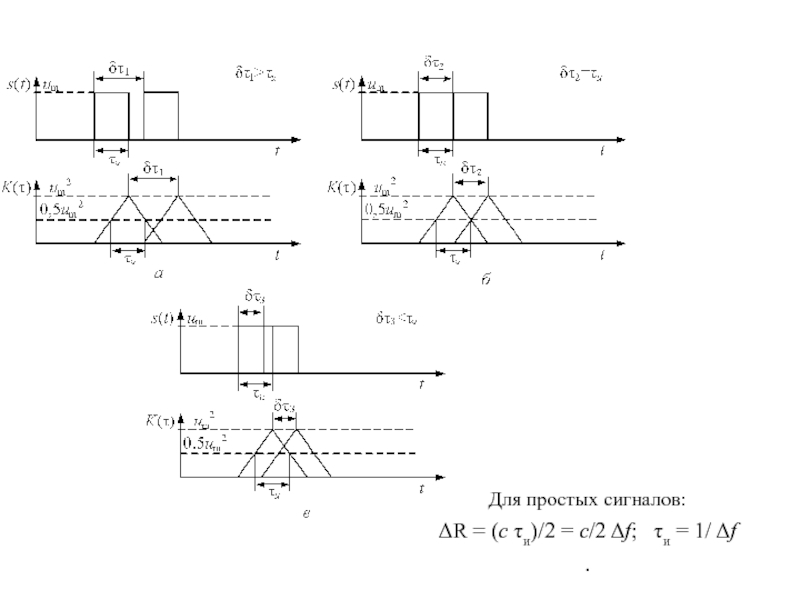
Слайд 8Для простых сигналов:
ΔR = (с τи)/2 = с/2 Δf;
τи = 1/ Δf
.
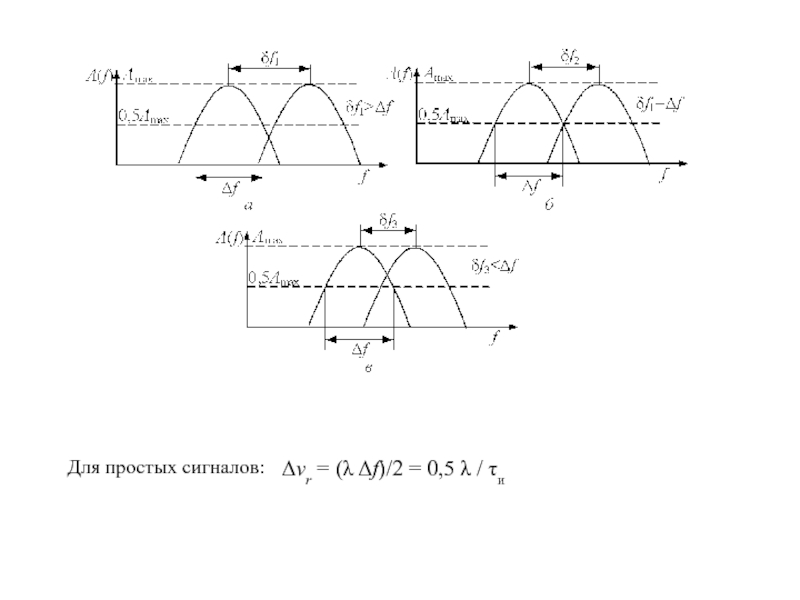
Слайд 9Δvr = (λ Δf)/2 = 0,5 λ / τи
Для простых
сигналов:
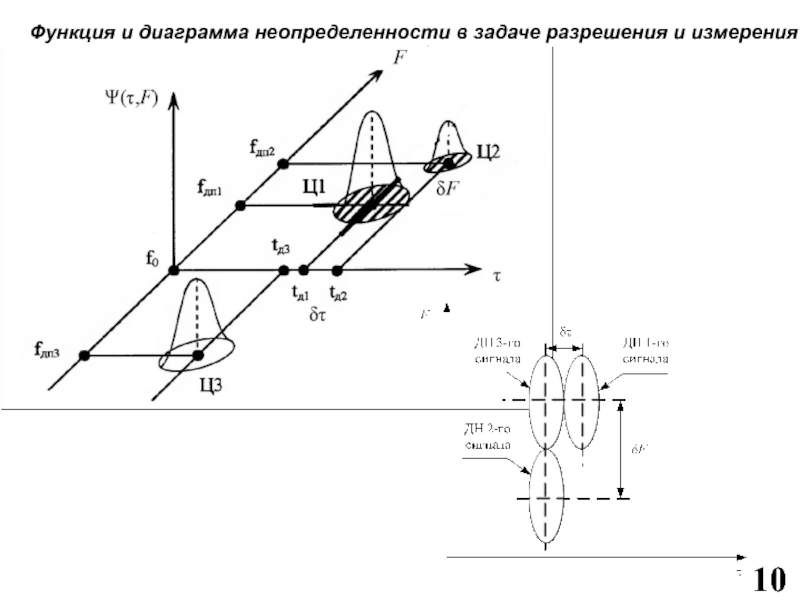
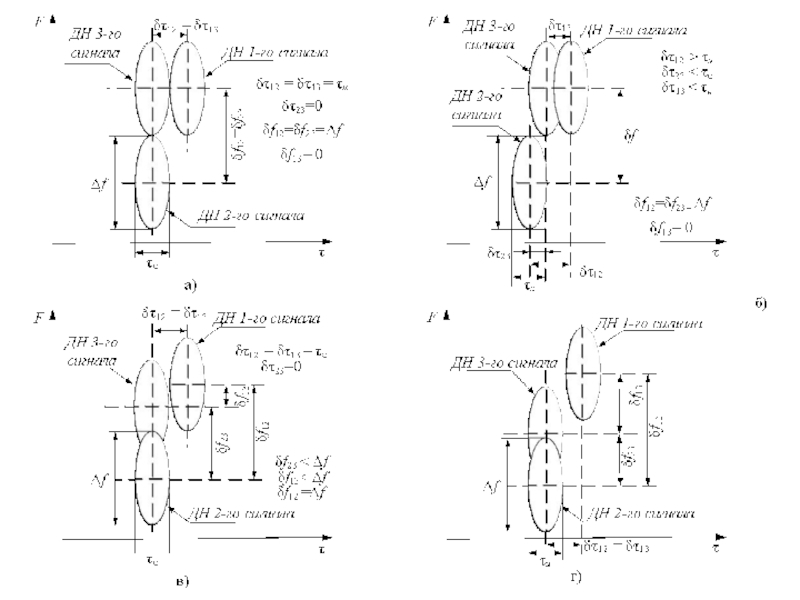
Слайд 10Функция и диаграмма неопределенности в задаче разрешения и измерения
Слайд 13Разновидности ШПС:
- с непрерывной модуляцией:
1)линейно-частотно-модулированные;
2)многочастотные;
- дискретно-кодированные сигналы:
1) кодированные по амплитуде (АДКС);
2) кодированные по частоте (ЧДКС) (сигналы Костаса); дискретные составные частотные.
3)
кодированные по фазе (фазо-кодо-модулированные (ФКМ), фазоманипулированные (ФМ)). (Бинарная (BPSK) ФМн-2: (коды Баркера; псевдослучайные последовательности, в частности М-последовательности, коды Кассами, коды Голда, коды Уолша-Адамара); ФМн-4; многофазные (коды Чу, коды Фрэнка).
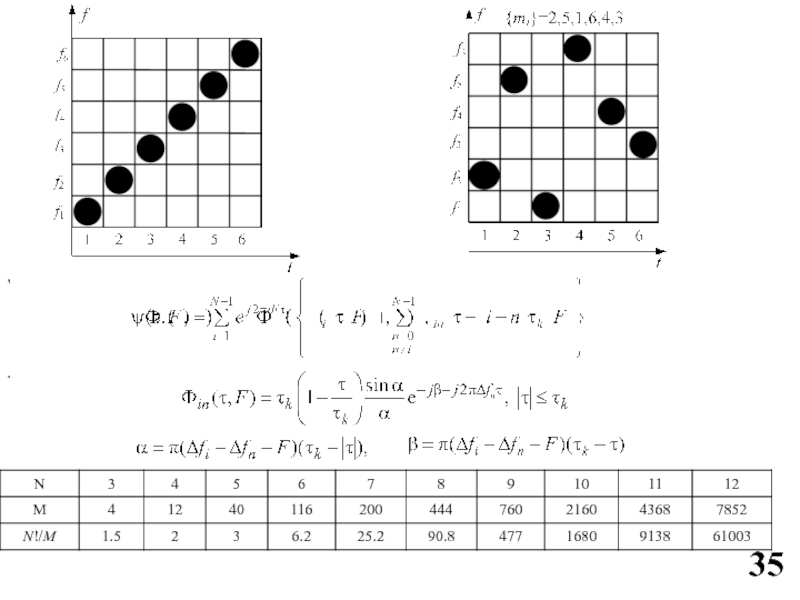
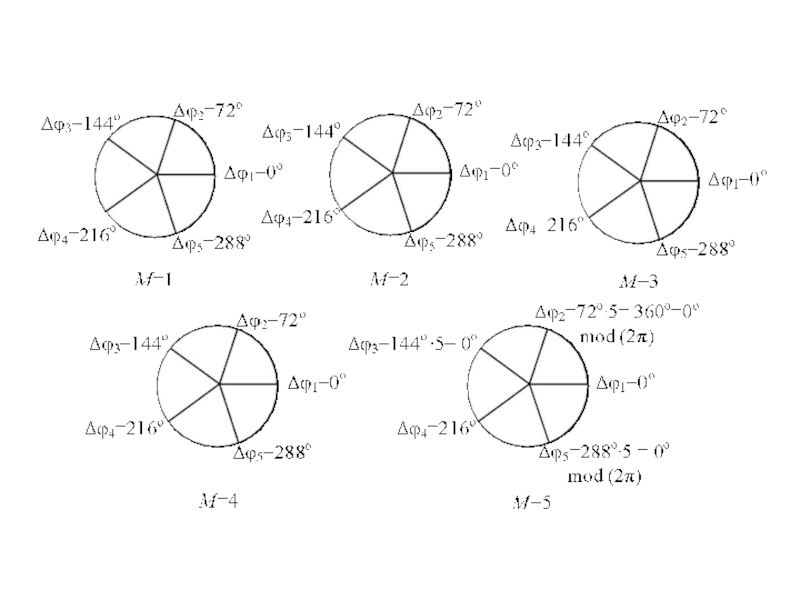
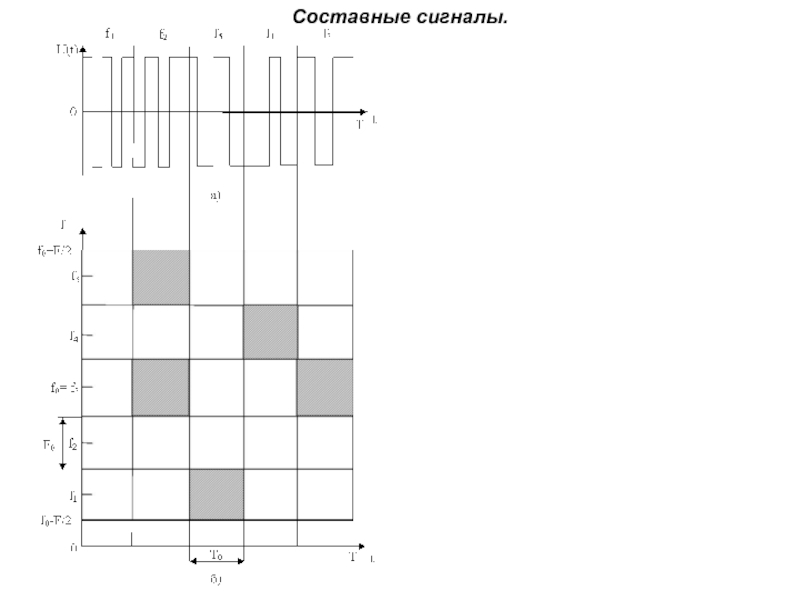
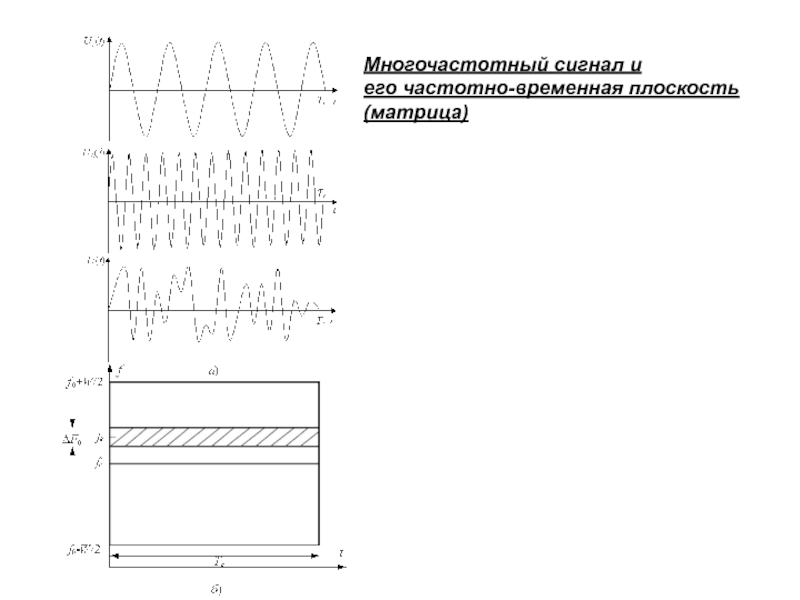
Слайд 14Многочастотный сигнал и
его частотно-временная плоскость
(матрица)
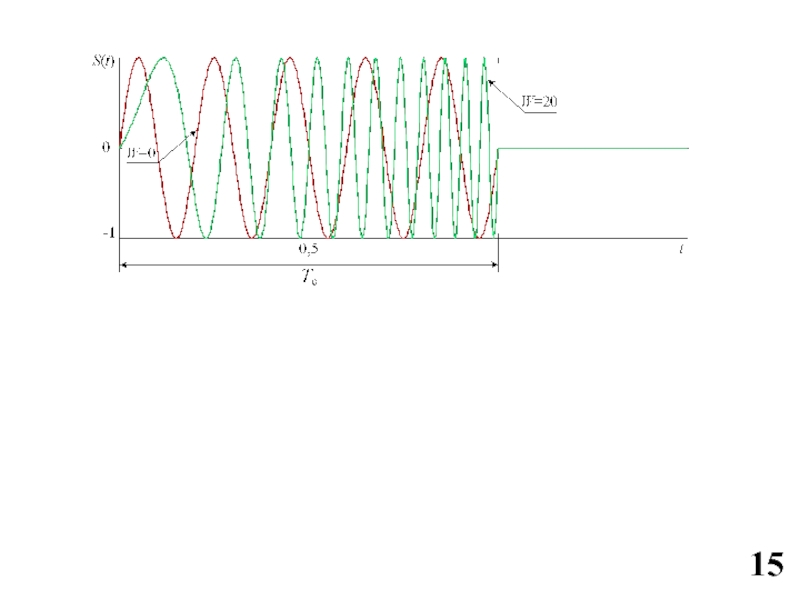
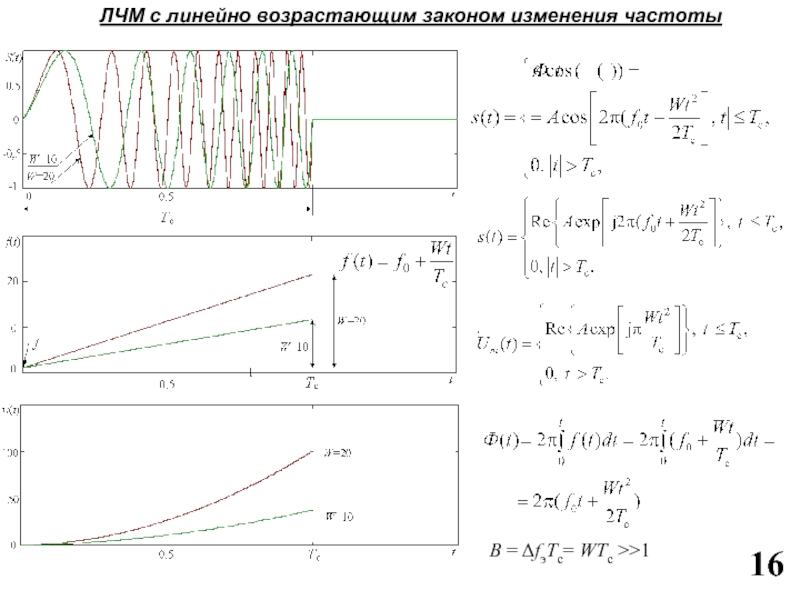
Слайд 16ЛЧМ с линейно возрастающим законом изменения частоты
B = ΔfэTc= WTc
>>1
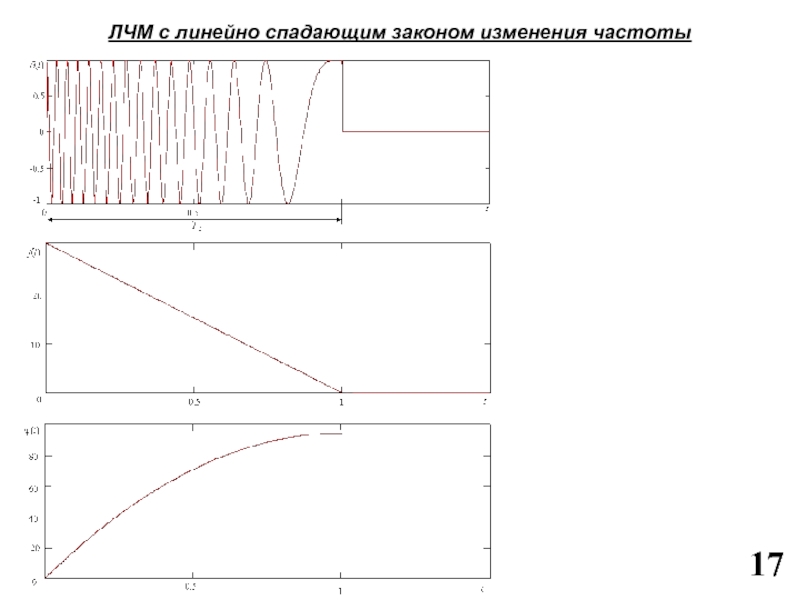
Слайд 17ЛЧМ с линейно спадающим законом изменения частоты
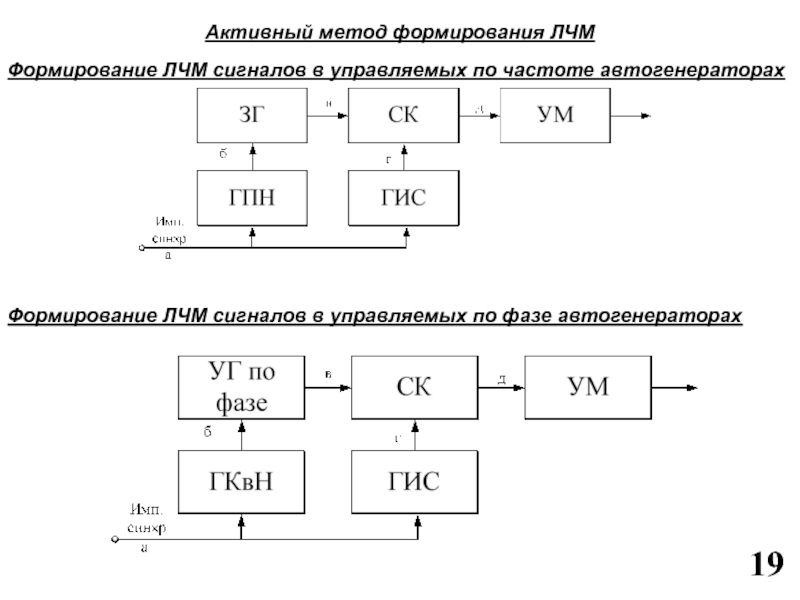
Слайд 19Активный метод формирования ЛЧМ
Формирование ЛЧМ сигналов в управляемых по частоте
автогенераторах
Формирование ЛЧМ сигналов в управляемых по фазе автогенераторах
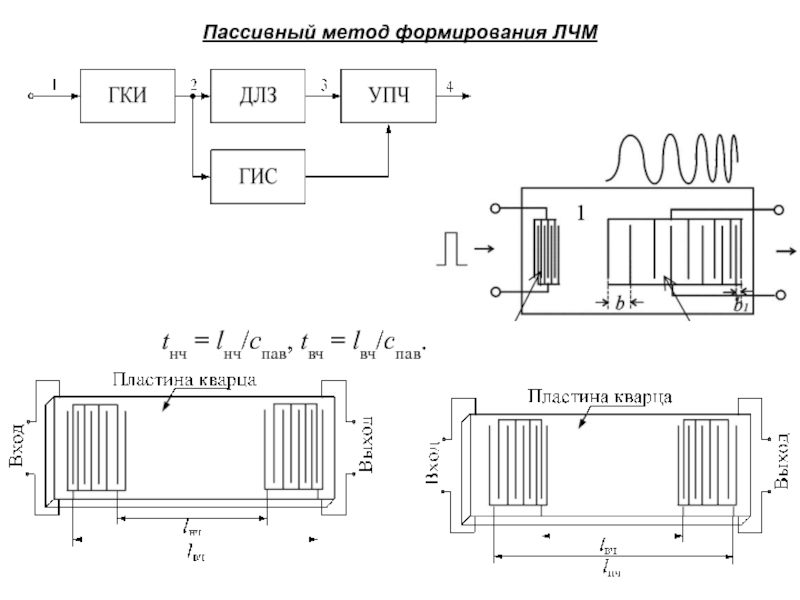
Слайд 20Пассивный метод формирования ЛЧМ
tнч = lнч/cпав, tвч = lвч/cпав.
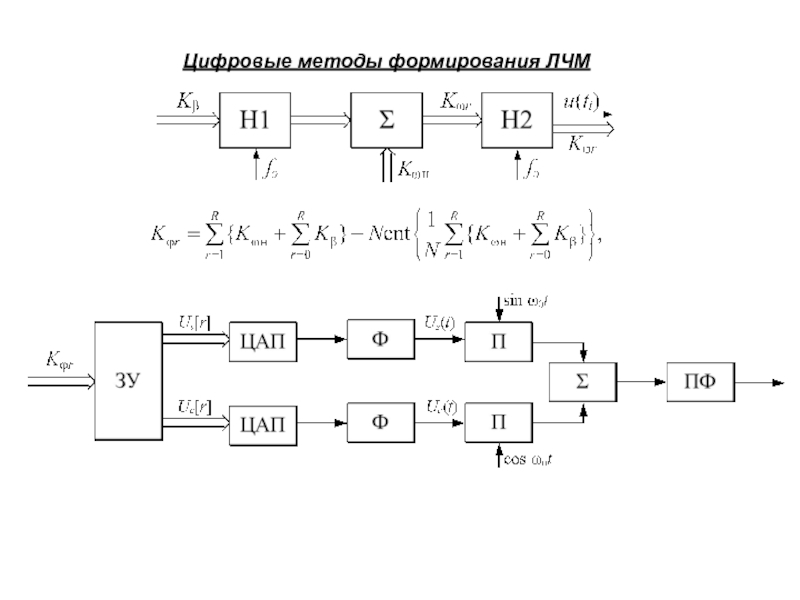
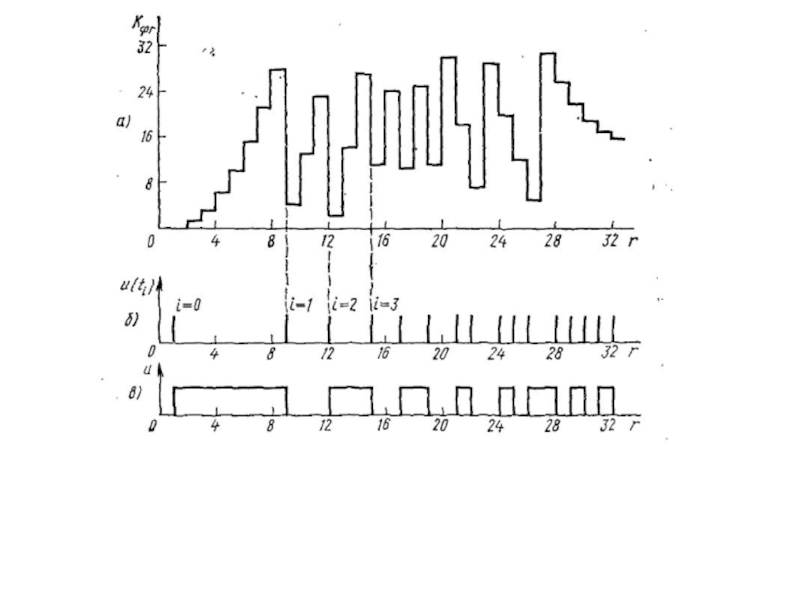
Слайд 21Цифровые методы формирования ЛЧМ
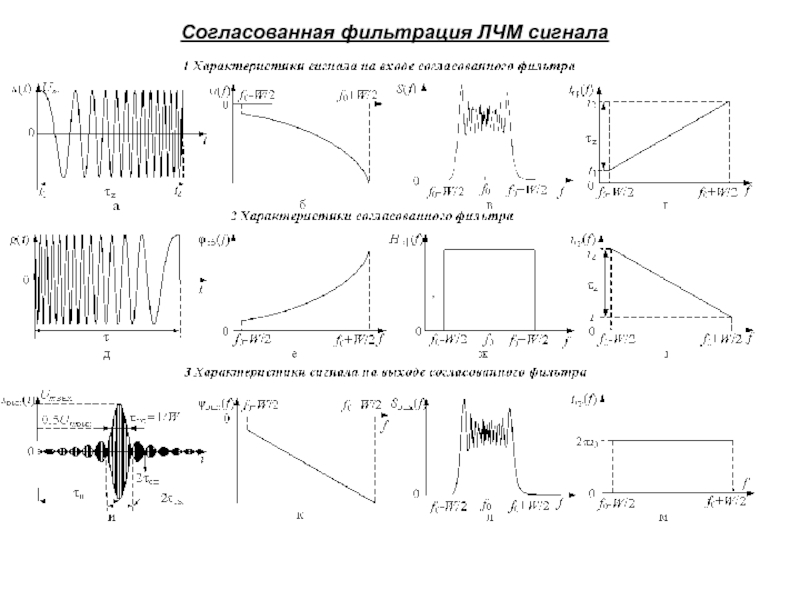
Слайд 23Согласованная фильтрация ЛЧМ сигнала
,
Слайд 24С учетом некоторых допущений фазовый и амплитудный спектры ЛЧМ сигнала
: ψ(f) ≈– πτи(f– f0)2/2W,S(f) ≈ Um τи /(2
)
Групповое время замедления спектральных составляющих ЛЧМ сигнала:
tгр(f) = – dψ(f)/df = πτи (f – f0)/W.
Амплитудный спектр сигнала на выходе СФ: Sвых(f) = Hсф(f) S(f) ≈ a Um τи /(2 )
Фазочастотная характеристика φсф(f)= – ψ(f) – 2πft0 СФ обратна по знаку фазовому спектру
входного сигнала, поэтому фазовый спектр выходного сигнала СФ:
ψвых(f) = ψ(f) + φсф(f) = – 2πft0,
где t0 – постоянная временная задержка фильтра t0> τи.
Групповое время замедления спектральных составляющих выходного сигнала:
tгр(f) = – dψвых(f)/df = – d(–2πft0)/df = 2πt0.
Сигнал на выходе СФ [автокорреляционная функция (АКФ)]определяется операцией свертки
входного сигнала s(t) с импульсной характеристикой (ИХ) g(t):
Увеличение амплитуды сжатого импульса Umвых можно определить из закона сохранения
энергии.
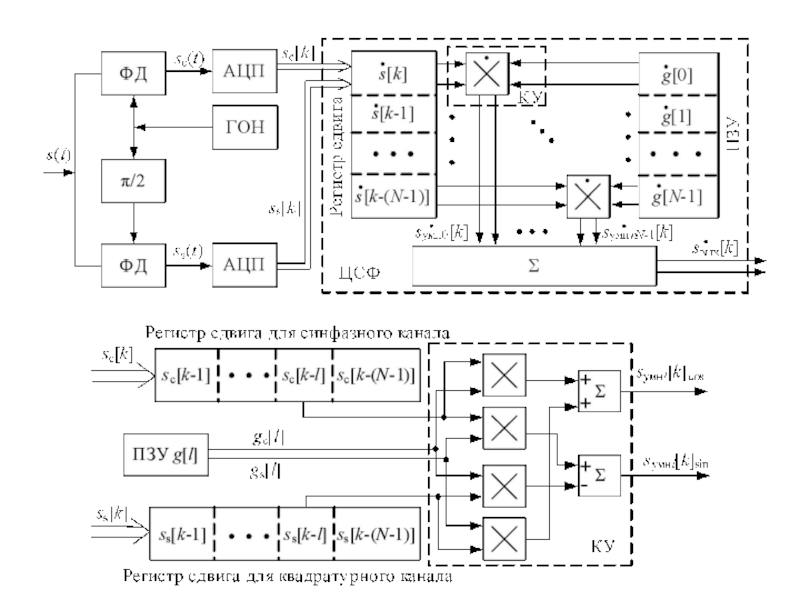
Слайд 26s(t) = sс(t) +jss(t) = Um(cos (πbt2)+ j sin (πbt2)).
b = W/τи
sс[k] = Umcos(πb [k]2), ss[k] = Umsin(πb[k]2)
k=0..N–1
g[l] = а s*[N–l],
g[l] = gс[l]+ j gs[l] = Um (cos(πb [N – l]2) – j sin(πb [N – l]2)),
sумнl[k]=s*[(N–l)] s[(k–l)] =
sумнl[k]cos +jsумнl[k]sin=
= Um2((cos(πb [N – l]2) – j sin(πb [N – l]2) (cos(πb [k –l]2)+ j sin(πb[k –l]2)))
sумнl[k]cos = Um2(cos(πb [N – l]2) cos(πb [k – l]2) + sin(πb [N – l]2)sin(πb[k –l]2)),
sумнl[k]sin = Um2(cos(πb [N – l]2) sin(πb[k – l]2) – sin(πb [N– l]2) cos(πb [k –l]2)).
Слайд 27Sвх[i] =
G[i] =
Sвых[i] = Sвх[i] G[i]
sвых[k] =
.
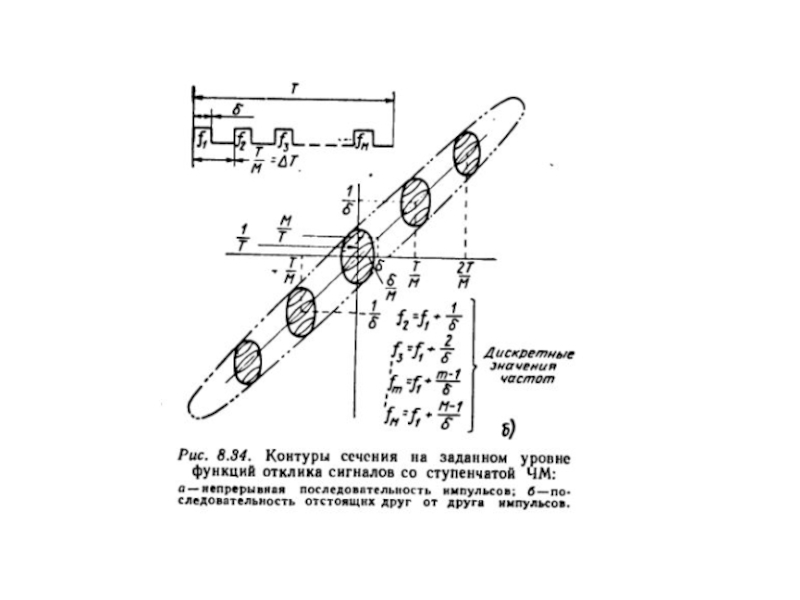
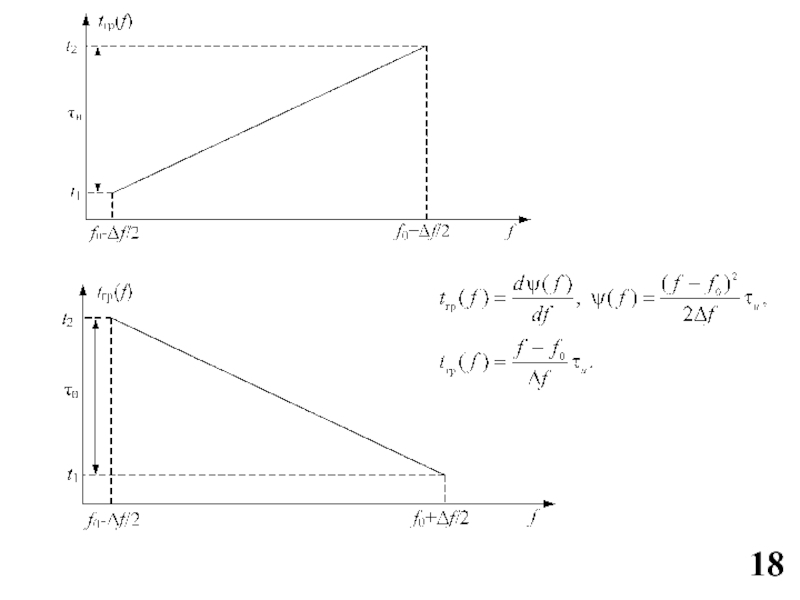
Слайд 28– временное смещение Δτ = Fд/b – для линейно убывающего закона изменения
частоты; Δτ = – Fд/b – для линейно возрастающего;
– амплитуда основного лепестка уменьшается
пропорционально
(1 – Fд /W);
– ширина основного лепестка по уровню 0,5:
Δτвыхν= 1/(W– |Fд|).
Слайд 29θ2 = - arctg(W/τи) – для линейно убывающего закона изменения частоты(1); θ1 = arctg(W/τи)
– для линейно возрастающего (2).
Для ЛЧМ сигнала разрешение по
дальности и скорости РЛС соответственно:
ΔR = cτи/2B = cτсж /2 = с/2W,
Δvr = (λΔf)/2 = 0,5λ/τи.
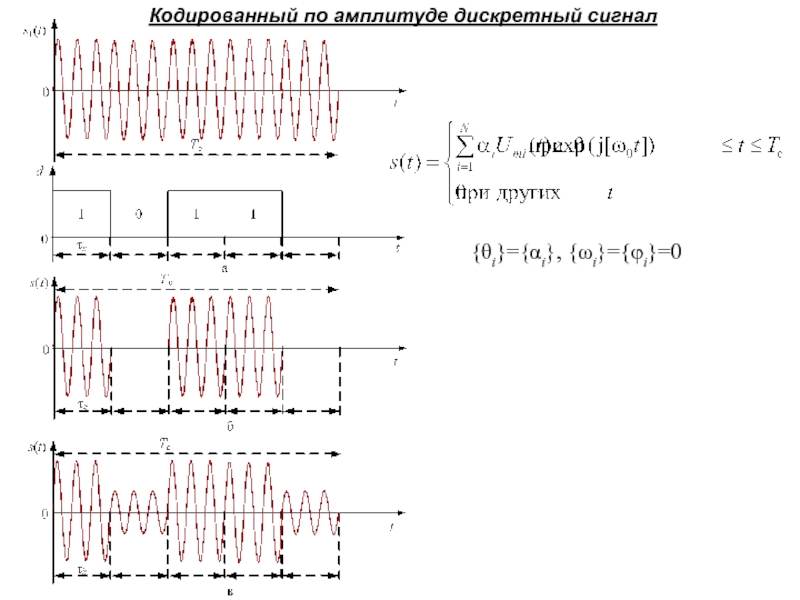
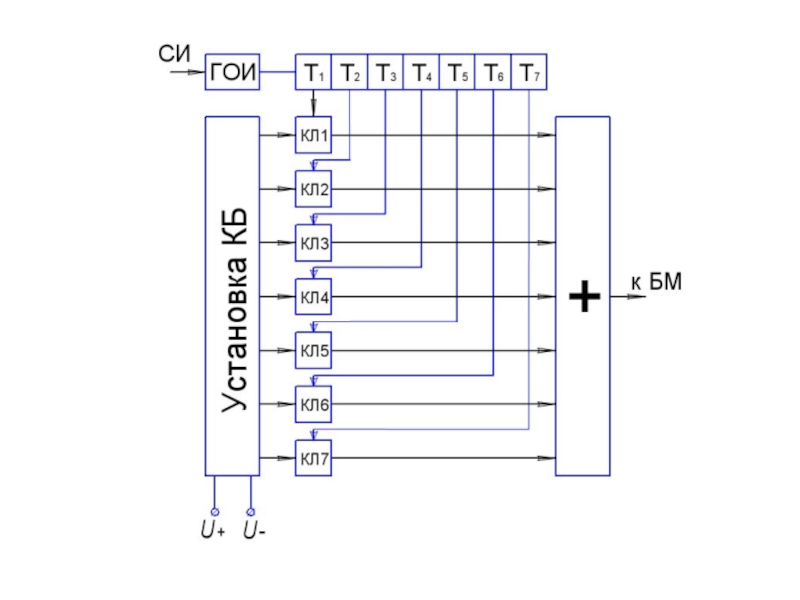
Слайд 33Кодированный по амплитуде дискретный сигнал
{θi}={αi}, {ωi}={φi}=0
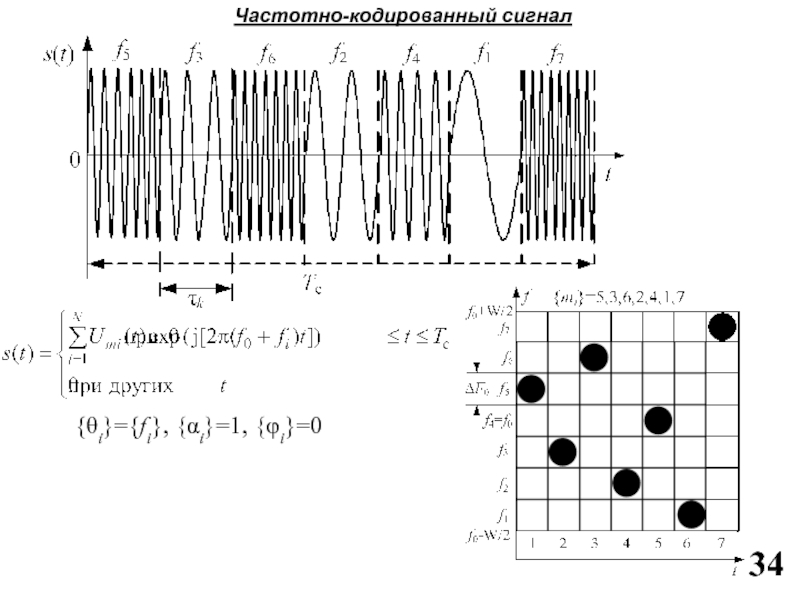
Слайд 34{θi}={fi}, {αi}=1, {φi}=0
Частотно-кодированный сигнал
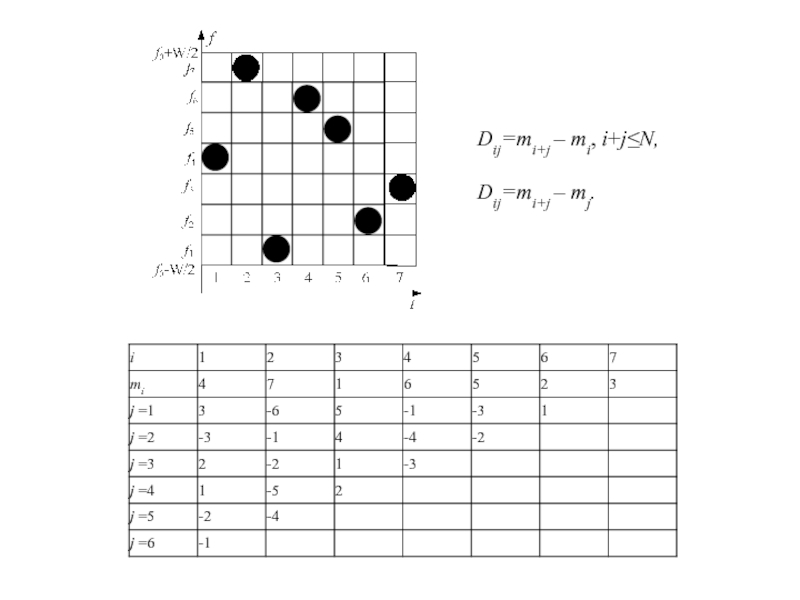
Слайд 36Dij=mi+j – mi, i+j≤N,
Dij=mi+j – mj.
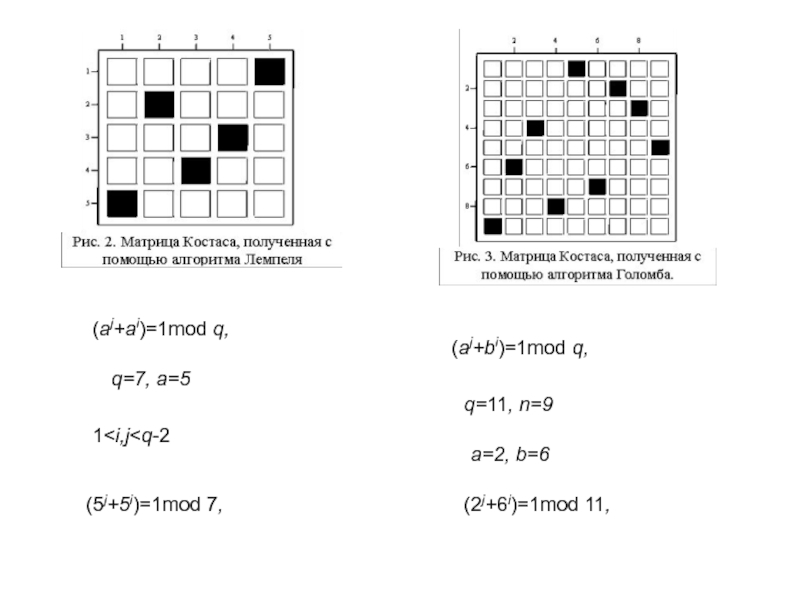
Слайд 39Алгоритмы Голомба, Уэлча и Лемпеля
Для произвольного простого числа p>2 конструкция Уэлча
дает (n x n) массив Костаса W1 с n=p-1 и массив W2 с n=p-2. Для некоторых простых чисел
можно построить массив Костаса W3 с n=p-3.
Эти конструкции используют таблицу логарифмов поля G(p), где p – нечетное простое число, а основание а является примитивным элементом этого поля.
Теорема Уэлча: «Пусть q – примитивный корень по модулю простого целого числа p. В этом случае перестановочная матрица размером (p-1)х(p-1) с аI,j=1 тогда и только тогда, когда j=qimod p, 1j=qimod p,
q=2, p=11
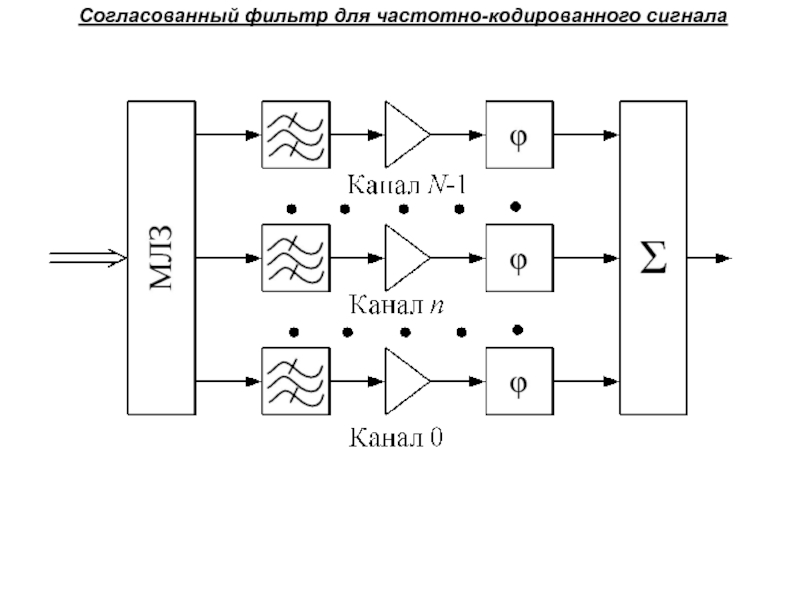
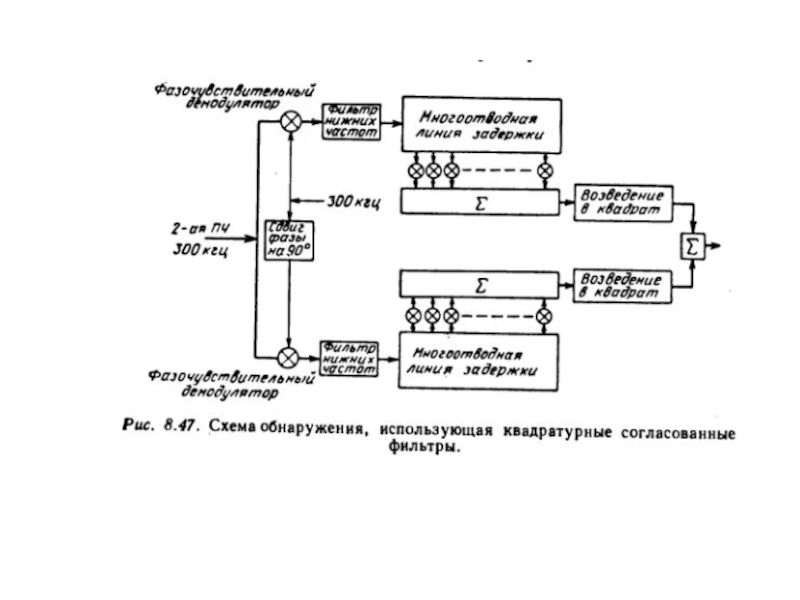
Слайд 41Согласованный фильтр для частотно-кодированного сигнала
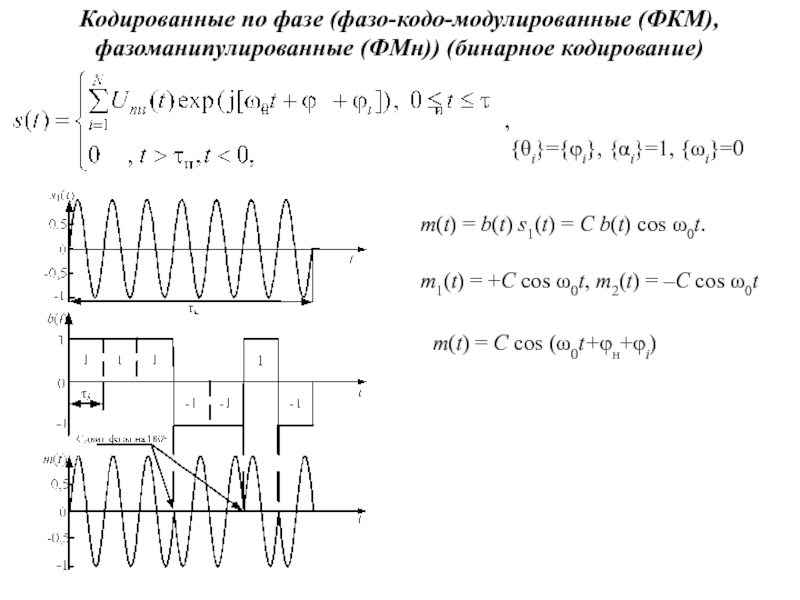
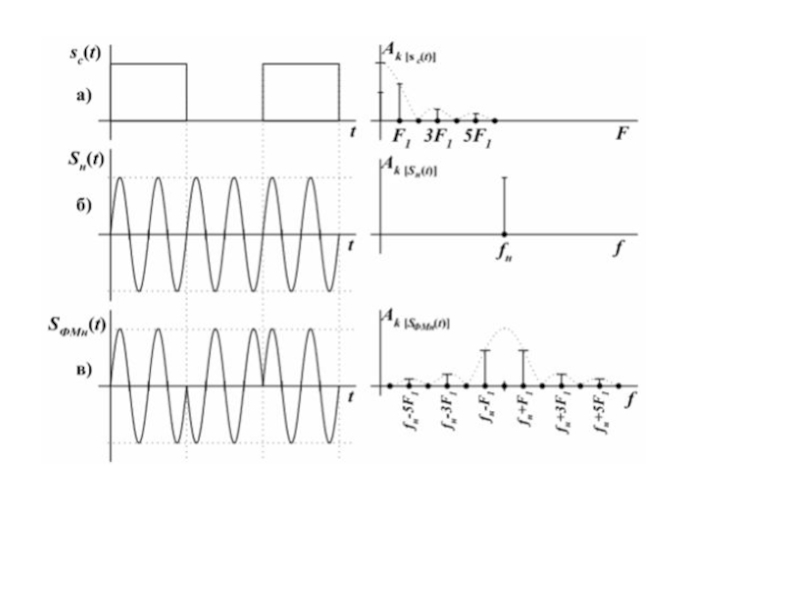
Слайд 43{θi}={φi}, {αi}=1, {ωi}=0
Кодированные по фазе (фазо-кодо-модулированные (ФКМ),
фазоманипулированные (ФМн)) (бинарное
кодирование)
m1(t) = +C cos ω0t, m2(t) = –C cos ω0t
m(t) = b(t) s1(t) = C b(t) cos ω0t.
m(t) = C cos (ω0t+φн+φi)
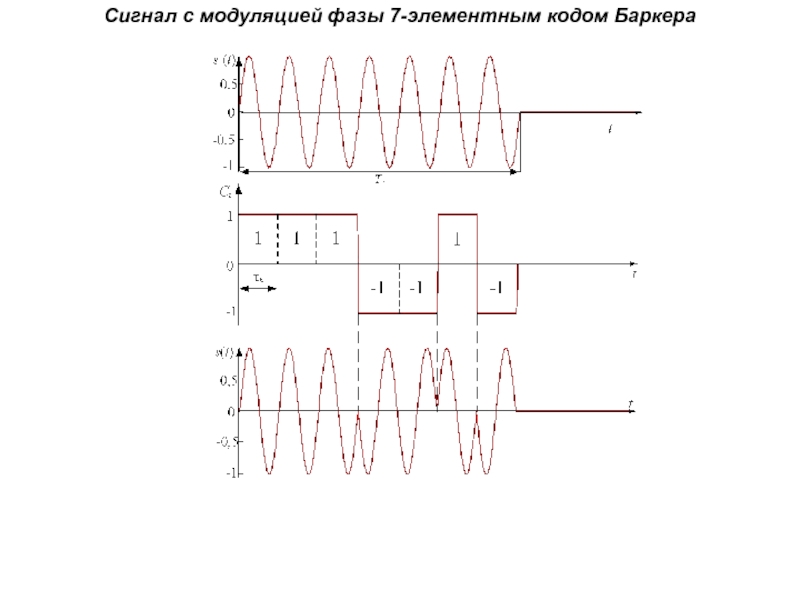
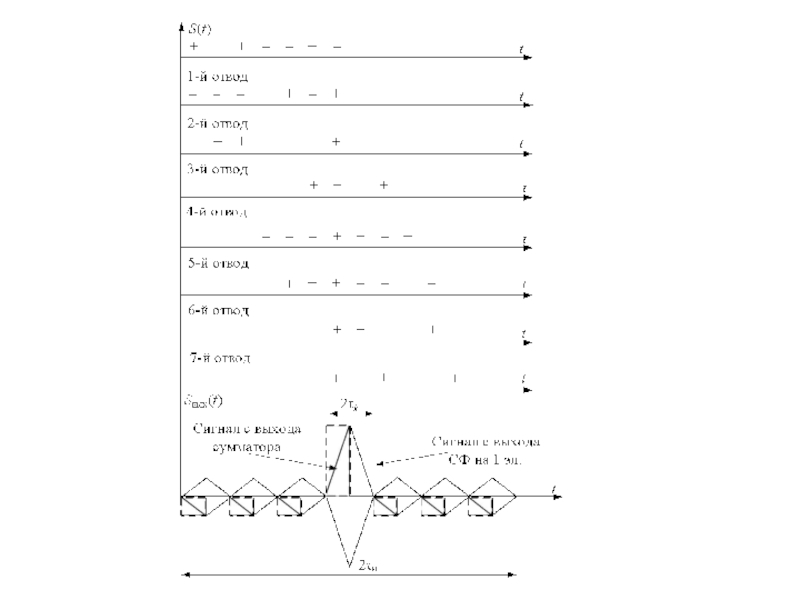
Слайд 47Сигнал с модуляцией фазы 7-элементным кодом Баркера
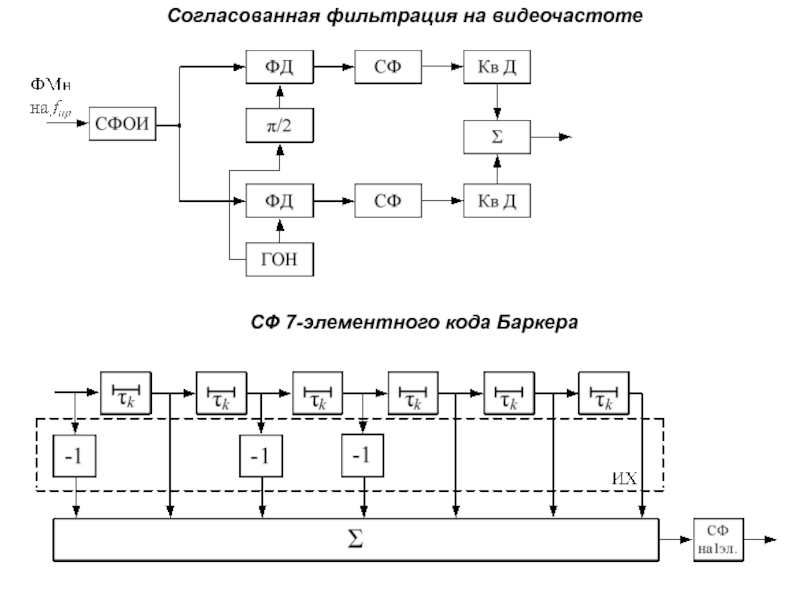
Слайд 49Согласованная фильтрация на видеочастоте
СФ 7-элементного кода Баркера
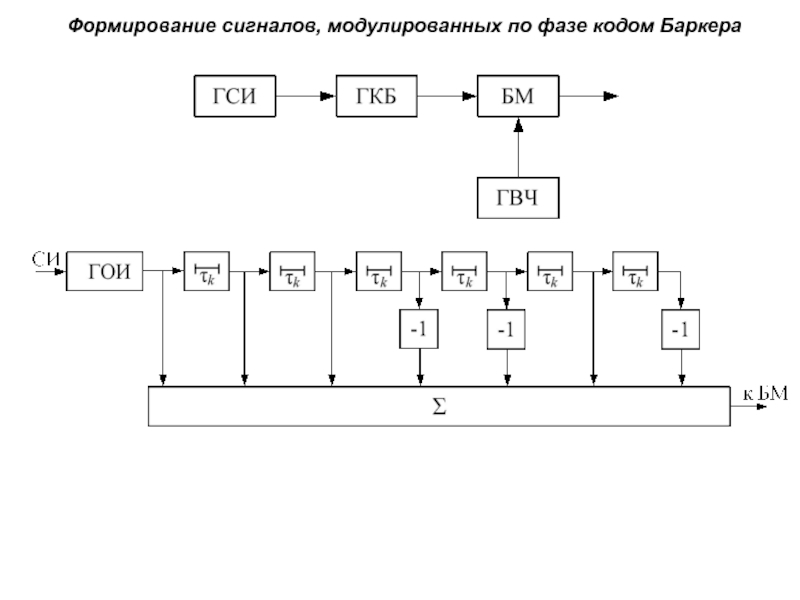
Слайд 52Формирование сигналов, модулированных по фазе кодом Баркера
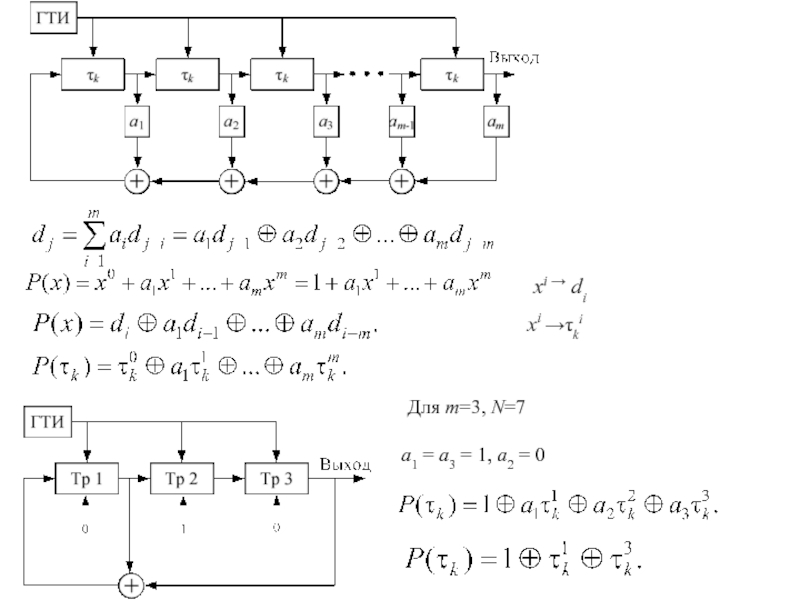
Слайд 54М-последовательности содержат 2m –1 элементов и имеют длительность Тс = τk(2m –1); так как
основание системы счисления (число различных символов) р = 2, а число разрядов
регистра и, то число возможных различных состояний регистра равно рm = 2m. Однако из всех возможных состояний регистра запрещено одно, представляющее собой m нулей, так как появление этой комбинации приводит к обращению в нуль символов во всех других комбинациях;
сумма 2-х М-последовательностей по модулю 2 является М-последовательностью;
любые комбинации символов длины n на длине одного периода М-последовательности за исключением комбинации из n нулей встречаются не более одного раза. Комбинация из n нулей является запрещенной: на ее основе может генерироваться только последовательность из одних нулей; последовательности на единицу больше, чем количество символов;
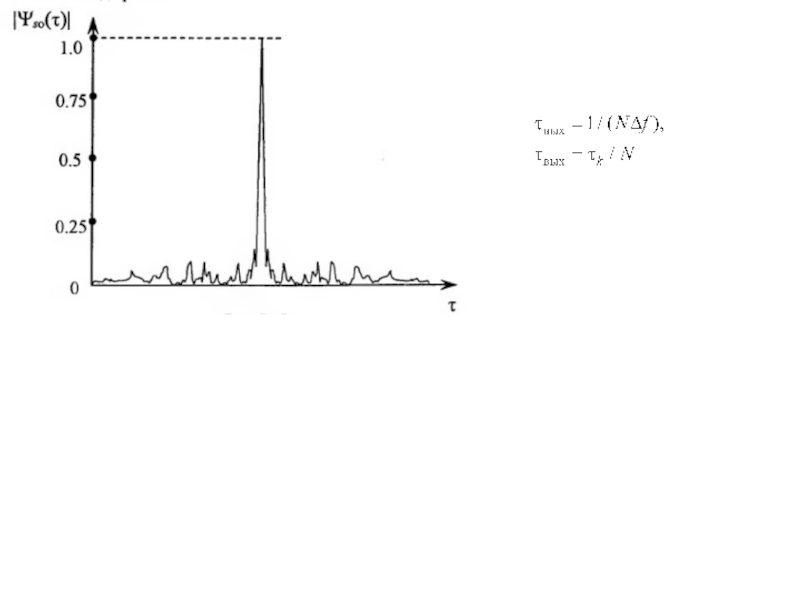
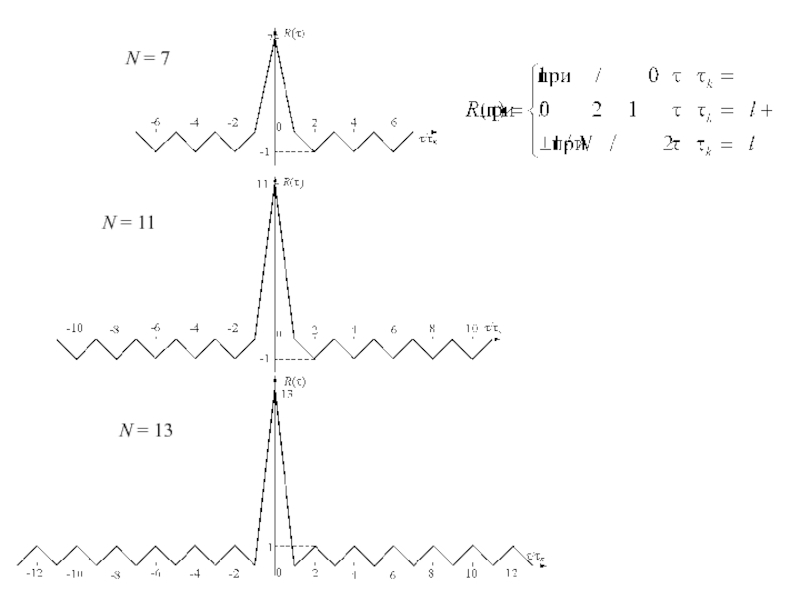
УБЛ АКФ периодической М-последовательности равен 1/N ; УБЛ АКФ усеченной М-последовательности, под которой понимается непериодическая последовательность длиной в период N, близок к 1/
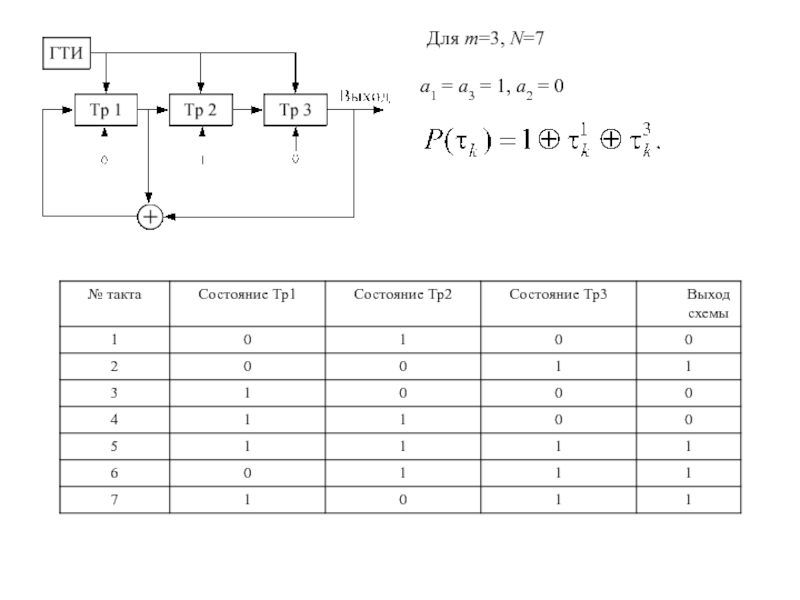
Слайд 55xi di
xi τki
Для m=3, N=7
a1 = a3 = 1,
a2 = 0
Слайд 57Правила синтеза схемы формирования М-последовательности на регистре сдвига:
1) число ячеек
регистра m= lg(N+1)/lg 2, где N определяется требуемым уровнем боковых
лепестков АКФ;
2) количество обратных связей определяется не равными 0 коэффициентами ai;
3) суммирование слагаемых производится по модулю 2;
4) последовательность смены кодовых символов определяется начальным блоком кода, т.е. начальной установкой символов бинарного кода в ячейке регистра;
5) В каждом периоде последовательности общее число единиц отличается от общего числа нулей не более чем на 1.
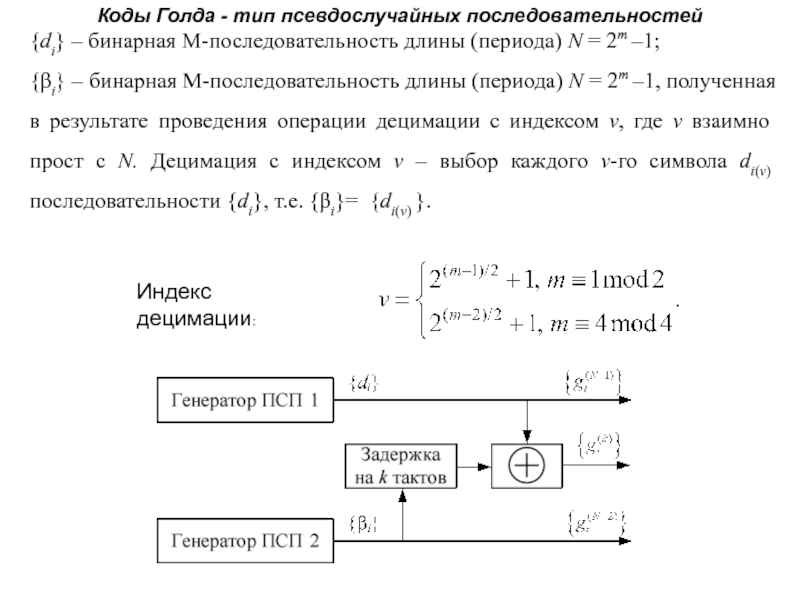
Слайд 58Индекс децимации:
Коды Голда - тип псевдослучайных последовательностей
{di} – бинарная
М-последовательность длины (периода) N = 2m –1;
{βi} – бинарная М-последовательность
длины (периода) N = 2m –1, полученная в результате проведения операции децимации с индексом v, где v взаимно прост с N. Децимация с индексом v – выбор каждого v-го символа di(v) последовательности {di}, т.е. {βi}= {di(v) }.
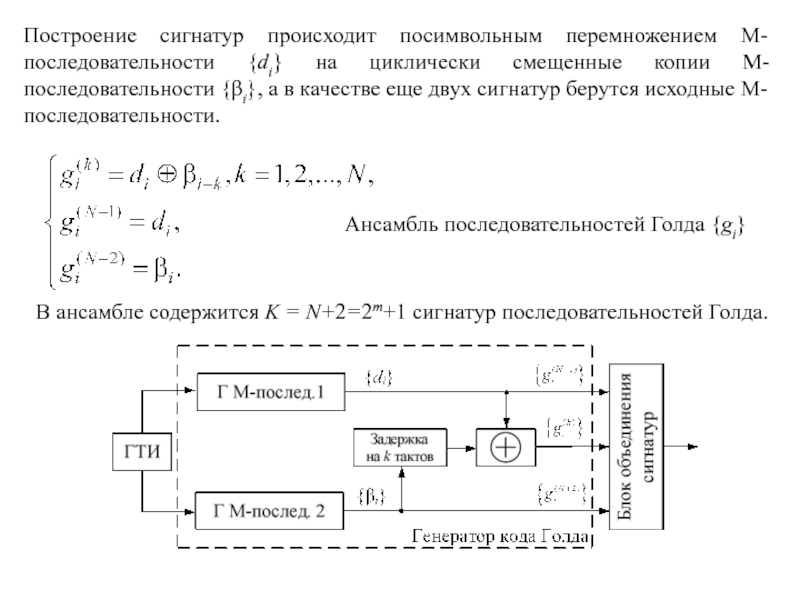
Слайд 59Ансамбль последовательностей Голда {gi}
В ансамбле содержится K = N+2=2m+1 сигнатур последовательностей
Голда.
Построение сигнатур происходит посимвольным перемножением М-последовательности {di} на циклически
смещенные копии М-последовательности {βi}, а в качестве еще двух сигнатур берутся исходные M-последовательности.
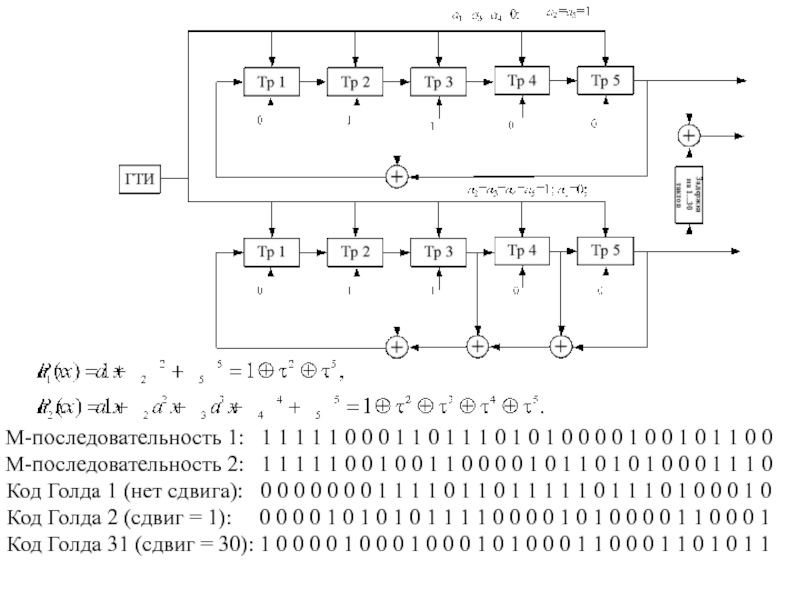
Слайд 60М-последовательность 1: 1 1 1 1 1 0 0
0 1 1 0 1 1 1 0 1 0
1 0 0 0 0 1 0 0 1 0 1 1 0 0
М-последовательность 2: 1 1 1 1 1 0 0 1 0 0 1 1 0 0 0 0 1 0 1 1 0 1 0 1 0 0 0 1 1 1 0
Код Голда 1 (нет сдвига): 0 0 0 0 0 0 0 1 1 1 1 0 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 0 0 1 0
Код Голда 2 (сдвиг = 1): 0 0 0 0 1 0 1 0 1 0 1 1 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 0 0 1
Код Голда 31 (сдвиг = 30): 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 1 1 0 0 0 1 1 0 1 0 1 1
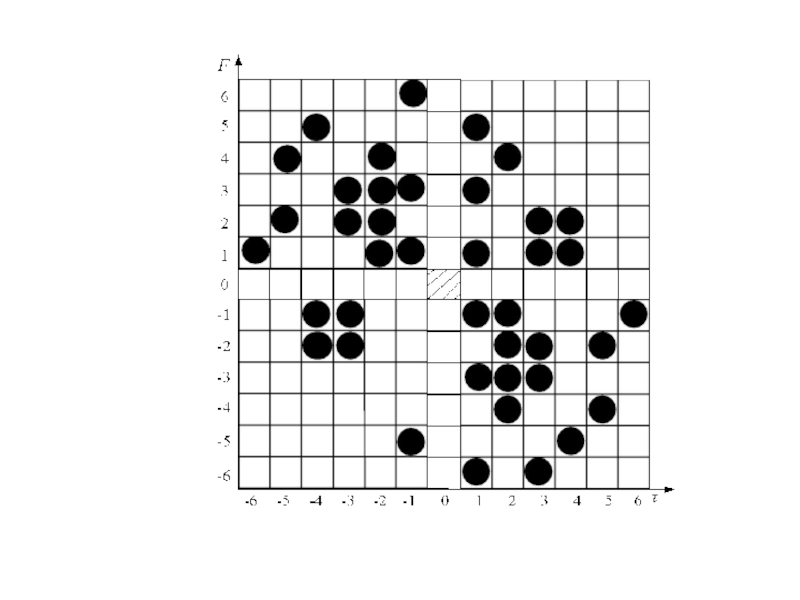
Слайд 61Корреляционный пик ансамбля Голда:
боковые лепестки нормированной периодической КФ:
для первого
варианта –
для второго варианта –
Для вариантов взаимосвязанных параметров m
и v :
1) m – нечетное число, v = 2s +1, s взаимно просто с m;
2) m – четное число, не кратное четырем, v = 2s +1, s четно и взаимно просто с m/2;
Слайд 62В GPS системе в качестве грубого кода используется код Голда,
сформированный из 2-х M-последовательностей с образующими полиномами:
Обе M-последовательности имеют
одинаковую таковую частоту и период.
Для получения дальномерного кода эти последовательности складываются
по модулю 2:
где ni – количество символов, задающее фазовый сдвиг кода i-го спутника.
Включение члена niτk в дальномерный код связано с применяемой в системе GPS кодовой (структурной) селекции сигналов спутников.
В основе выделения ШПС требуемого НИСЗ лежит образование корреляционной функции с формируемым в аппаратуре потребителя кодом, соответствующим выбранному спутнику. Поэтому коды, присвоенные каждому из спутников, должны быть ортогональными, т.е. давать ВКФ, близкую к нулю, и обладать низким УБЛ корреляционной функции для уменьшения взаимных помех.
Ортогональность кодов достигается выбором ni, т.е. сдвигом кода по фазе. Из всей совокупности кодов Голда (1025) выбирают 37 и присваивают их соответствующим спутникам системы.
Слайд 63В системе ГЛОНАСС сигналы спутников идентифицируются по несущей частоте. В
диапазонах L1 и L2 частоты формируется по правилу, fk = f0+kΔf, где
f0 – номинальное значение несущей частоты, Δf = 0,5 MГц – интервал между несущими частотами, соседних по частоте спутников; k =1,2,..24. Общий для всех НИСЗ системы ГЛОНАСС грубый дальномерный код формируется с помощью образующего полинома М-последовательности:
Слайд 64Коды Касами
{di} – бинарная М-последовательность длины (периода) N = 2m –1.
Проводится
операция децимации с индексом v, где v невзаимно прост с
N, которая означает выбор каждого v-го символа di(v) последовательности {di} и запись выбранных символов друг за другом в новую последовательность {βi} с периодом, значение которого является делителем N, где βi= di(v).
В процессе создания v = 2m/2 последовательностей Касами выборки берутся через каждые v = 2m/2+1 (v = 2p+1) элементов М-последовательности, чтобы сформировать периодическую последовательность и с дальнейшим суммированием по модулю 2 этой последовательность постепенно с первоначальной М-последовательности. Доказано, что при соблюдении некоторых условий на начальное значение последовательности {di} «короткая» последовательность {βi} является бинарной М-последовательностью периодом N1=2p–1, p=m/2.
Слайд 65Ансамбль последовательностей Касами {ksi}
Ансамбль последовательностей Касами содержит N1 сигнатур
Касами длины N, которые образуются посимвольным сложением по модулю 2
исходной «длинной» M-последовательности с N1 циклическими копиями {βi}, а еще одной сигнатурой служит сама «длинная» последовательность.
K = N1 +1 = 2p=
Слайд 66Для последовательностей Касами боковые лепестки нормированной периодической КФ принимает три
возможных значения:
Сравнение двух бинарных ансамблей показывает выигрыш множеств Касами
в уровне корреляционного пика у ансамблей Голда той же длины в обмен на значительно меньшее количество сигнатур в ансамбле.
Слайд 67{di}= {1,0,0,0,1,0,0,1,1,0,1,0,1,1,1}
{βi}={1,0,1,1,0,1,1,0,1,1,0,1,1,0,1}
Построим ансамбль Касами длины N=24–1=15 (p = 2, K=
=4).
Начнем с бинарной M-последовательности
{di} длины N=15 на основе примитивного полинома P(x) = 1+аx+а4x4 с начальным состоянием регистра сдвига с обратной связью Tr4 =1, Tr2 = Tr3 = Tr1 = 0. Децимация последовательности с индексом v=2p+1=5 дает M-последовательность периода три {βi}. Сумма по модулю 2 последовательности {di} с тремя сдвинутыми копиями {βi} после перехода образует первые три сигнатуры Касами
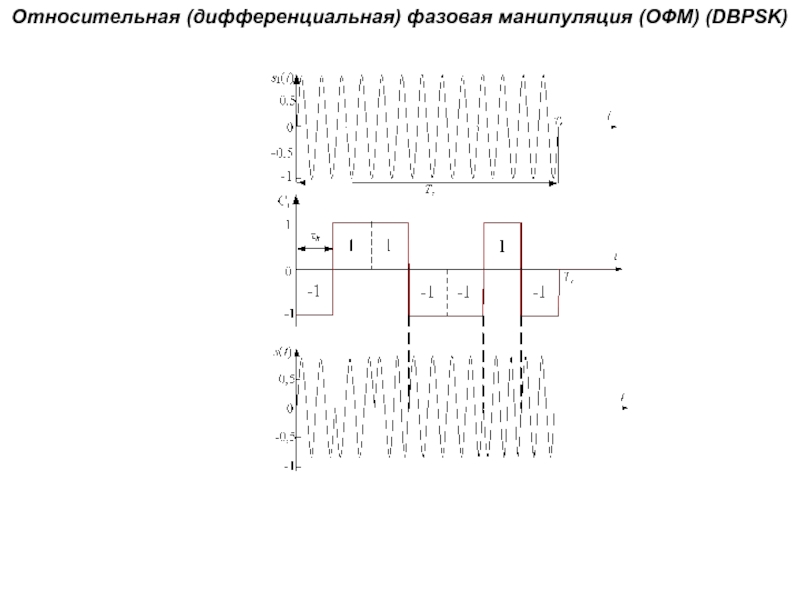
Слайд 69Относительная (дифференциальная) фазовая манипуляция (ОФМ) (DBPSK)
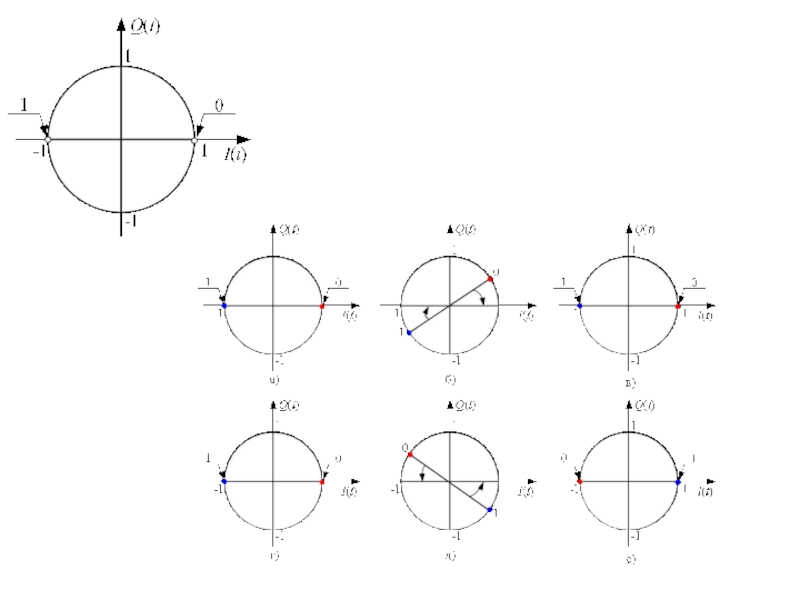
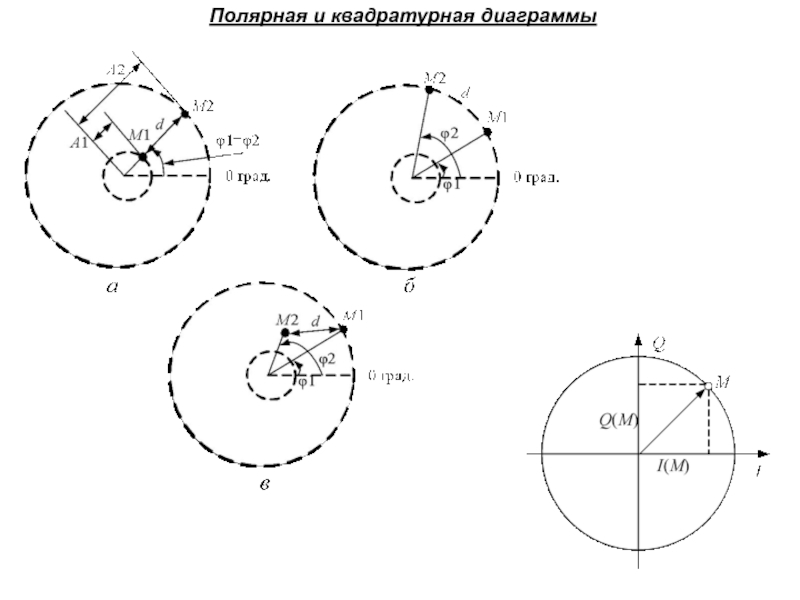
Слайд 70Полярная и квадратурная диаграммы
Слайд 71Многопозиционная фазовая манипуляция
М – количество позиций фазы.
E = A2T/2,
.
Для
QPSK сигнала:
Ik=±1 и Qk=±1,
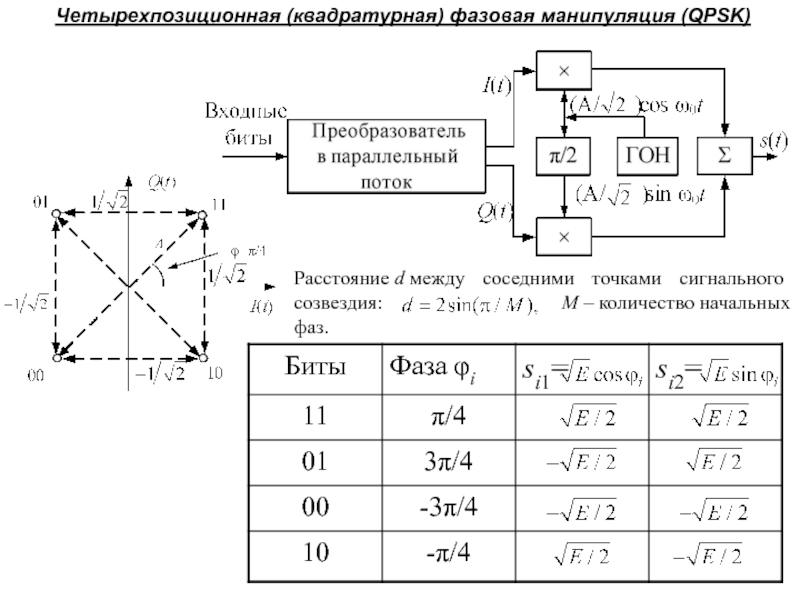
Слайд 72Четырехпозиционная (квадратурная) фазовая манипуляция (QPSK)
Расстояние d между соседними точками сигнального созвездия:
M – количество начальных фаз.
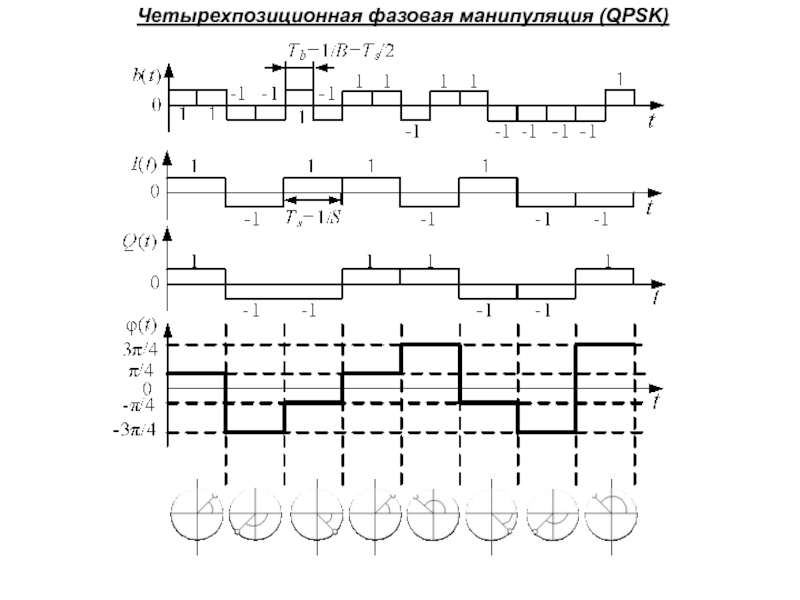
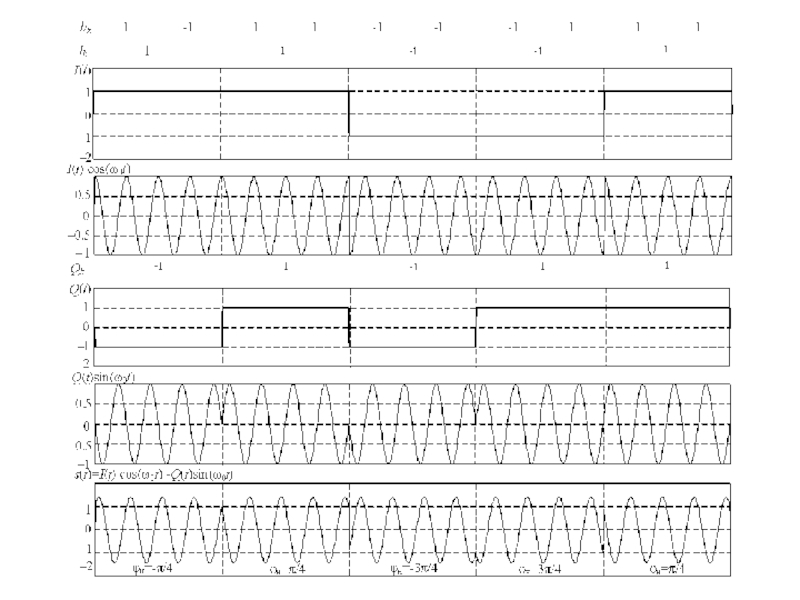
Слайд 73Четырехпозиционная фазовая манипуляция (QPSK)
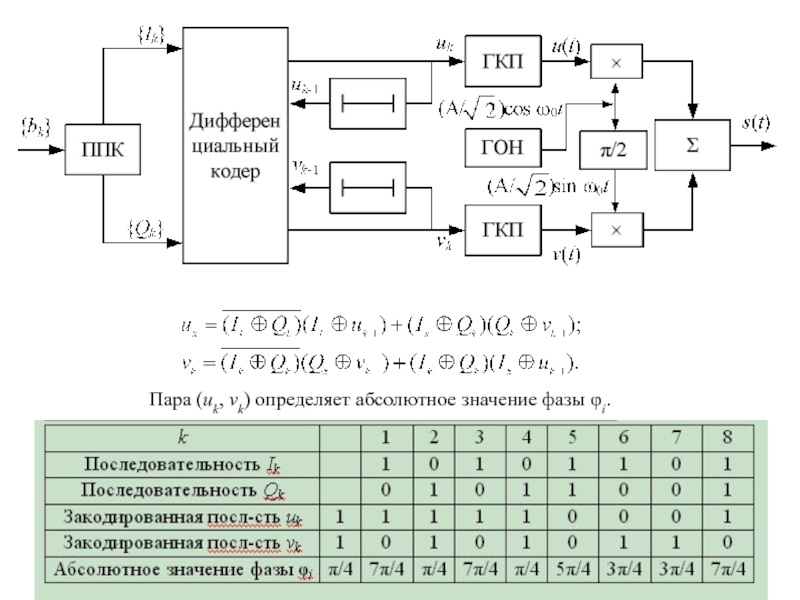
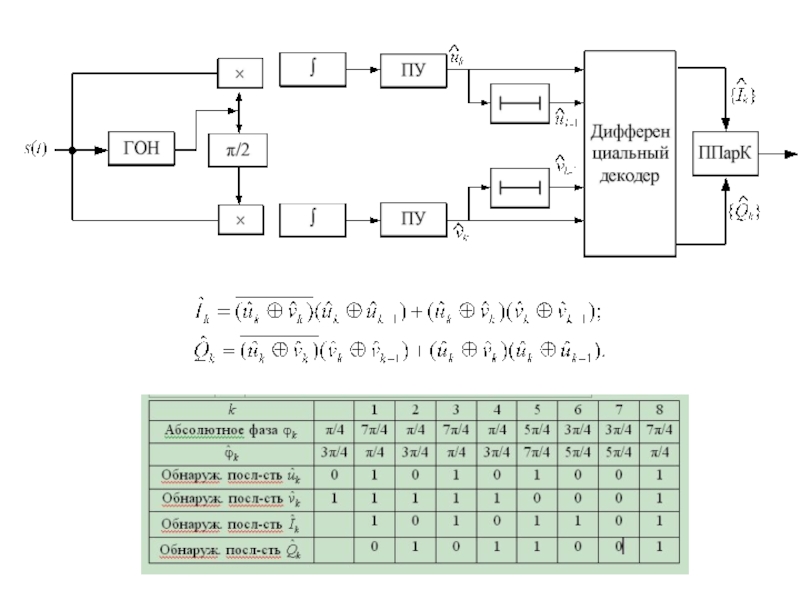
Слайд 75Относительная (дифференциальная) квадратурная фазовая манипуляция
(DQPSK)
.
Слайд 76Пара (uk, vk) определяет абсолютное значение фазы φi.
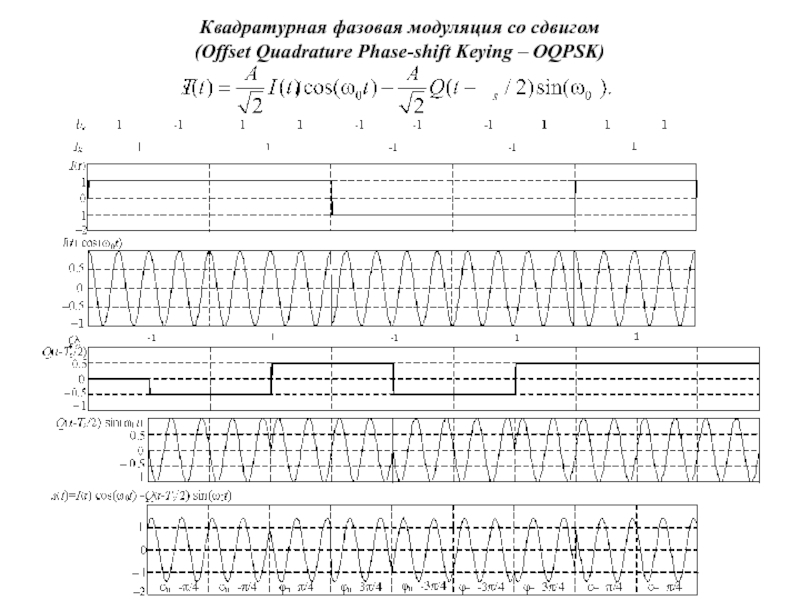
Слайд 78Квадратурная фазовая модуляция со сдвигом
(Offset Quadrature Phase-shift Keying –
OQPSK)
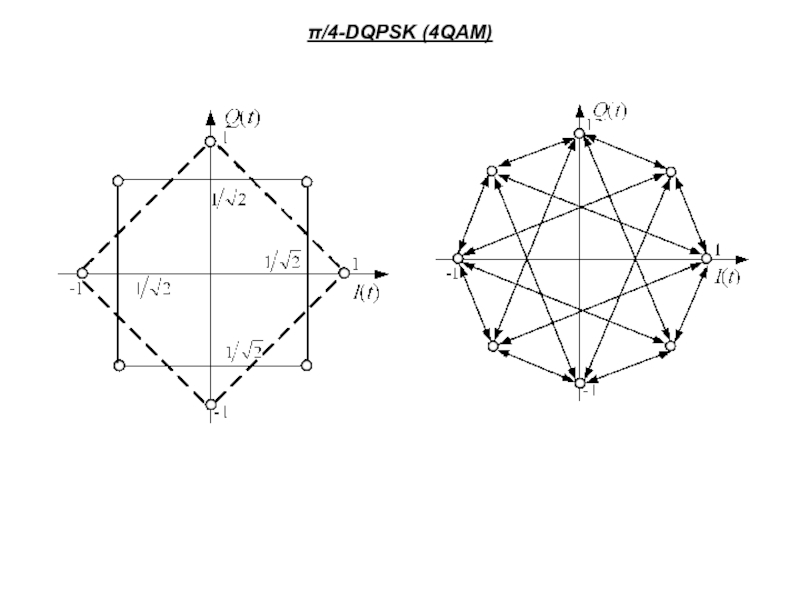
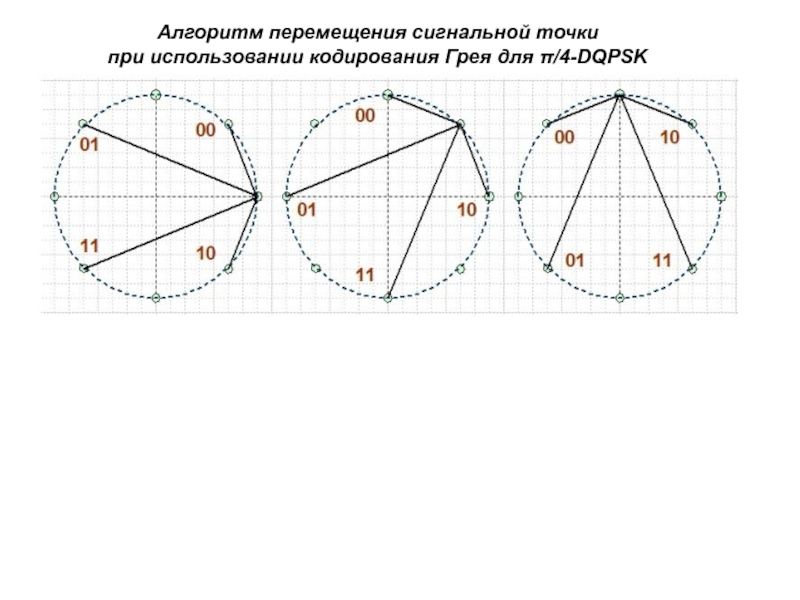
Слайд 80Алгоритм перемещения сигнальной точки
при использовании кодирования Грея для π/4-DQPSK
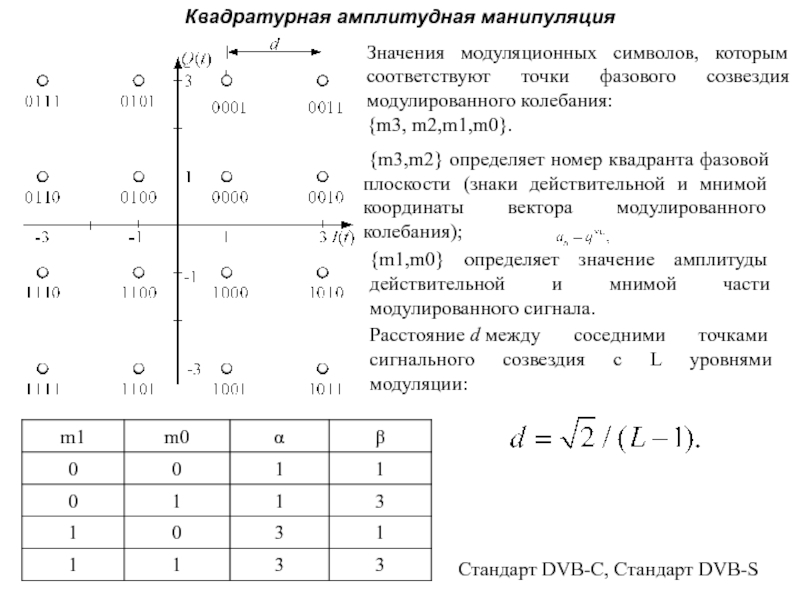
Слайд 81Стандарт DVB-C, Стандарт DVB-S
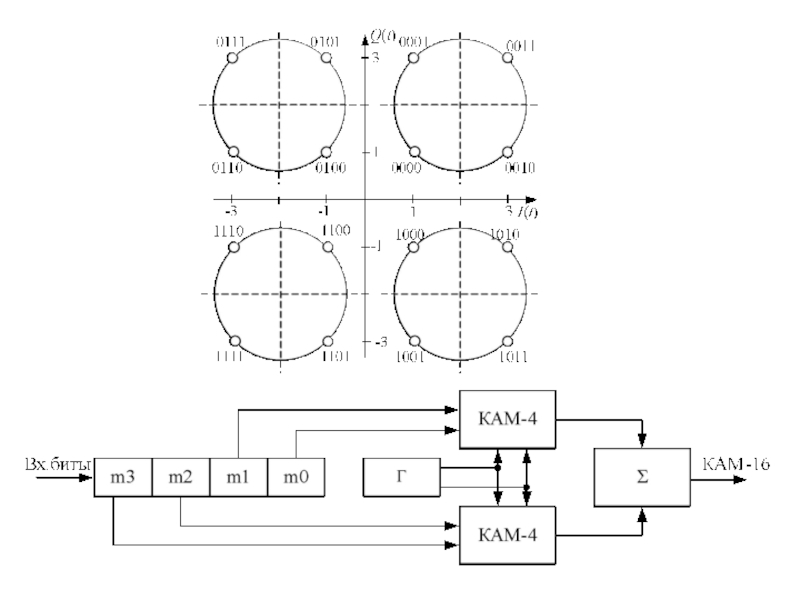
Значения модуляционных символов, которым соответствуют точки
фазового созвездия модулированного колебания:
{m3, m2,m1,m0}.
{m3,m2} определяет номер квадранта
фазовой плоскости (знаки действительной и мнимой координаты вектора модулированного колебания);
Квадратурная амплитудная манипуляция
{m1,m0} определяет значение амплитуды действительной и мнимой части модулированного сигнала.
Расстояние d между соседними точками сигнального созвездия с L уровнями модуляции:
Слайд 83Многофазное кодирование. Коды Фрэнка.
Для M=3, p=1.
Каждый элемент матрицы B –
произведение νμ,
ν, μ = 0, 1, …, M –1,
ν – номер строки, μ – номер столбца.
Количество элементов кода: N =М 2, где М – целое число.
Символы сигналов Фрэнка an , n = 1…N: an=qνμ ,
где q = exp (j2πp/M)), р – число, взаимно простое с М, а νμ произведения определяются квадратной матрицей порядка М:
:
Номер элементов по индексу n определяется, начиная с левого верхнего элемента
по строкам, выписывая строку за строкой. Номер символа: n = νμ + μ +1.
Последовательность символов в сигнале в записи по правилу присоединения:
Фаза ν-гo элемента в μ-ой последовательности:
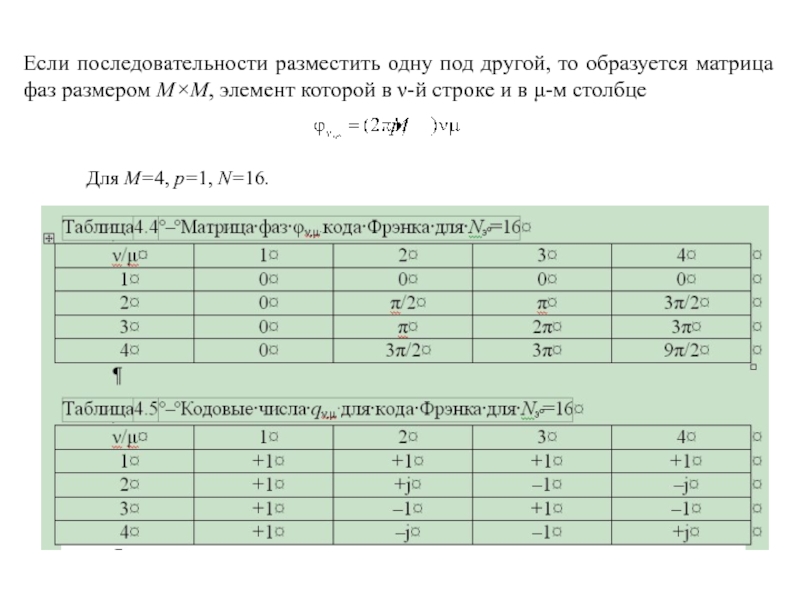
Слайд 84Для M=4, p=1, N=16.
Если последовательности разместить одну под другой, то
образуется матрица фаз размером М×М, элемент которой в ν-й строке
и в μ-м столбце
Слайд 85Изменение фазы в отличие от двоичного кодирования осуществляется дискретными значениями
из набора конечного значения числа дискретов в пределах 360°.
Количество
дискретов фазы определяется:
Nφ=pn,
где р – простое целое число, n – целое число 1,2,...,n.
Например, при двоичном кодировании фазы N = 2 (0° и 180°), что соответствует значениям р = 2, п =1.
Если взять р = 5, n = 1, то получим 5 дискретных значений фазы равномерно распределенных в пределах 360°:
Общее количество элементов последовательности ШПС с многофазным кодом:
N = Nφr_1,
где r – количество кодовых состояний в генераторе псевдослучайного кода.
Последовательность ШПС с многофазной кодовой манипуляцией для Nφ=5 при r =2, общее число элементов последовательности равно N =24.





![Список литературы
по дисциплине Сложные сигналы в радиотехнических s(t) = sс(t) +jss(t) = Um(cos (πbt2)+ j sin (πbt2)). b = W/τи sс[k] = Umcos(πb [k]2), ss[k] = Umsin(πb[k]2) k=0..N–1 g[l] = а s*[N–l],g[l] = gс[l]+ j gs[l] = Um (cos(πb [N – l]2) – j sin(πb [N – l]2)), sумнl[k]=s*[(N–l)] s[(k–l)] = sумнl[k]cos +jsумнl[k]sin= = Um2((cos(πb [N – l]2) – j sin(πb [N – l]2) (cos(πb [k –l]2)+ j sin(πb[k –l]2))) sумнl[k]cos = Um2(cos(πb [N – l]2) cos(πb [k – l]2) + sin(πb [N – l]2)sin(πb[k –l]2)),sумнl[k]sin = Um2(cos(πb [N – l]2) sin(πb[k – l]2) – sin(πb [N– l]2) cos(πb [k –l]2)). s(t) = sс(t) +jss(t) = Um(cos (πbt2)+ j sin (πbt2)). b = W/τи sс[k] = Umcos(πb [k]2), ss[k] = Umsin(πb[k]2) k=0..N–1 g[l] = а s*[N–l],g[l] = gс[l]+ j gs[l] = Um (cos(πb [N – l]2) – j sin(πb [N – l]2)), sумнl[k]=s*[(N–l)] s[(k–l)] = sумнl[k]cos +jsумнl[k]sin= = Um2((cos(πb [N – l]2) – j sin(πb [N – l]2) (cos(πb [k –l]2)+ j sin(πb[k –l]2))) sумнl[k]cos = Um2(cos(πb [N – l]2) cos(πb [k – l]2) + sin(πb [N – l]2)sin(πb[k –l]2)),sумнl[k]sin = Um2(cos(πb [N – l]2) sin(πb[k – l]2) – sin(πb [N– l]2) cos(πb [k –l]2)).](/img/thumbs/9aff896fa510b315da6dd271294de832-800x.jpg)
![Список литературы
по дисциплине Сложные сигналы в радиотехнических Sвх[i] =G[i] = Sвых[i] = Sвх[i] G[i] sвых[k] = . Sвх[i] =G[i] = Sвых[i] = Sвх[i] G[i] sвых[k] = .](/img/thumbs/1329827baa6b7fac589f1794d2d52eb4-800x.jpg)