Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства функций, имеющих предел. Асимптоты графика функции и методы их отыскания.
Содержание
- 1. Свойства функций, имеющих предел. Асимптоты графика функции и методы их отыскания.
- 2. Свойства функций, имеющих предел. ТЕОРЕМА 1. Если функция f(x)
- 3. ТЕОРЕМА 2. Если функция f(x) имеет в
- 4. ТЕОРЕМА 3. Если f (x) ≥ 0 в
- 5. ТЕОРЕМА 4. (О двух милиционерах.) Если в
- 6. ТЕОРЕМА 5. Если f(x) = с –
- 7. ДОКАЗАТЕЛЬСТВО.Воспользуемся определением предела по Гейне. Возьмем ЧП
- 8. СЛЕДСТВИЯ из теорем 3, 5.Если f(x) ≥
- 9. Арифметика бесконечностей. Введем обозначения:С = const ≠
- 10. Неопределенные ситуации, требующие исследования. 0/0
- 11. Асимптоты графика функции.ОПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНОЙ АСИМПТОТЫ. Прямая х =
- 12. ОПРЕДЕЛЕНИЕ НАКЛОННОЙ АСИМПТОТЫ. Прямая у = kx +
- 13. Доказательство.Пусть Тогда f(x) – (kx + b) =
- 14. Пусть Тогда f(x) – (kx + b) = (f(x)
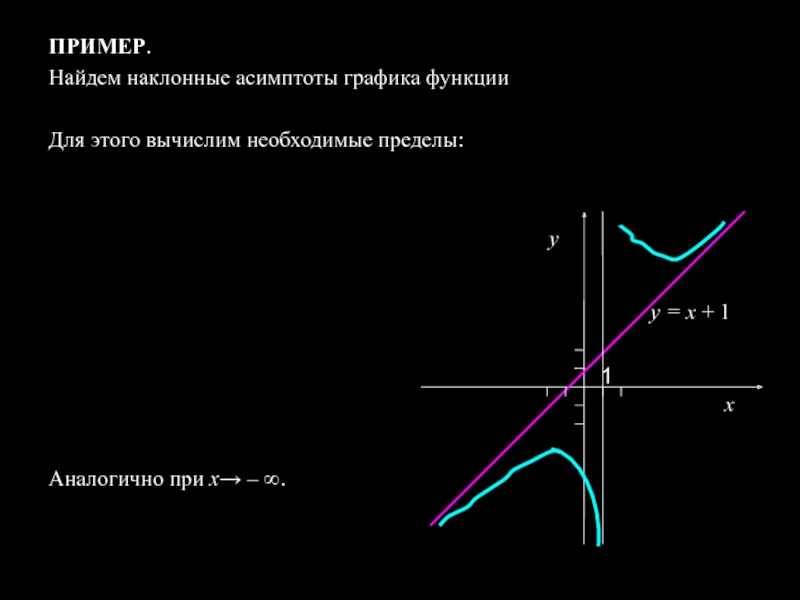
- 15. ПРИМЕР. Найдем наклонные асимптоты графика
- 16. СПАСИБО ЗА ВНИМАНИЕ!
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 2.2
Свойства функций, имеющих предел.
Асимптоты графика
функции и методы их отыскания.
Слайд 2Свойства функций, имеющих предел.
ТЕОРЕМА 1.
Если функция f(x) имеет предел в
точке а, то найдется такая проколотая окрестность точки а, в
которой функция ограничена.ДОКАЗАТЕЛЬСТВО.
Пусть
Тогда, по определению предела, для ε = 1 найдется такая проколотая δ-окрестность точки а , что для всех
выполняется неравенство
А – 1 < f(x) < А+1.
Это и означает ограниченность функции на множестве
Слайд 3 ТЕОРЕМА 2.
Если функция f(x) имеет в точке а предел,
отличный от нуля, то найдется такая проколотая окрестность точки а,
в которой функция сохраняет знак предела.ДОКАЗАТЕЛЬСТВО.
Пусть
Тогда, по определению предела, для
найдется такая проколотая δ-окрестность точки а , что
Если А > 0, то из левого неравенства ⇒
если А < 0, то из правого неравенства ⇒
Слайд 4ТЕОРЕМА 3.
Если f (x) ≥ 0 в некоторой проколотой окрестности
точки а и
то А ≥ 0.
ДОКАЗАТЕЛЬСТВО.
Воспользуемся определением предела
по Гейне. Возьмем числовую последовательность
Тогда
Следовательно, по соответствующей теореме для числовых последовательностей, А ≥ 0.
и f( xn ) ≥ 0 для всех n.
сходящуюся к а.
Слайд 5 ТЕОРЕМА 4. (О двух милиционерах.)
Если в некоторой проколотой окрестности
точки а справедливы неравенства f(x)
≤ g(x) ≤ ϕ(x)и существуют то
ДОКАЗАТЕЛЬСТВО.
Воспользуемся определением предела по Гейне. Возьмем
сходящуюся к а. Тогда
и f( xn) ≤ g( xn) ≤ ϕ ( xn) для всех n. Следовательно по теореме о двух
милиционерах для числовых последовательностей
т.е. существует
Слайд 6ТЕОРЕМА 5.
Если f(x) = с – постоянная в некоторой
проколотой окрестности точки а, то
Если существуют
тогда существуют и
Слайд 7ДОКАЗАТЕЛЬСТВО.
Воспользуемся определением предела по Гейне. Возьмем ЧП
сходящуюся к
а. Тогда f(xn) = с для всех n иследовательно
2. Воспользуемся определением предела по Гейне. Возьмем ЧП
сходящуюся к а. Тогда
по теореме о пределе суммы для ЧП
то есть
Слайд 8СЛЕДСТВИЯ из теорем 3, 5.
Если f(x) ≥ В в некоторой
проколотой окрестности точки а
и то А ≥ В.Если существует то для любого числа С
Слайд 9Арифметика бесконечностей.
Введем обозначения:
С = const ≠ 0.
∞ – бесконечно
большая функция произвольного знака;
+ ∞ – бесконечно большая положительная
функция; – ∞ – бесконечно большая отрицательная функция;
0 – бесконечно малая функция;
1 – функция, предел которой равен 1.
Тогда имеют место следующие соотношения:
С⋅∞ = ∞
С/0 = ∞
С/∞ = 0
+ ∞ + ∞ = + ∞
–∞ – ∞ = – ∞
(+∞)С = + ∞, если С>0 (0, если C < 0)
(+∞)+∞ = + ∞
Слайд 11Асимптоты графика функции.
ОПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНОЙ АСИМПТОТЫ.
Прямая х = а называется вертикальной
асимптотой графика функции f(x), если выполнено хотя бы одно из
условий:ПРИМЕР.
Прямая х = 1 является вертикальной
асимптотой графика функции
так как
Слайд 12 ОПРЕДЕЛЕНИЕ НАКЛОННОЙ АСИМПТОТЫ.
Прямая у = kx + b называется наклонной
асимптотой графика функции f(x) при х→ + ∞ (при х→
– ∞), еслиСПОСОБ ОТЫСКАНИЯ НАКЛОННОЙ АСИМПТОТЫ.
ТЕОРЕМА.
Прямая у = kx + b является наклонной асимптотой графика функции f(x) при х→ + ∞ (при х→ – ∞) тогда и только тогда, когда существуют конечные пределы
Слайд 13Доказательство.
Пусть
Тогда
f(x) – (kx + b) = α(х),
где α(х)
бесконечно малая при х→ + ∞. Отсюда получим, что
Слайд 14Пусть
Тогда
f(x) – (kx + b) = (f(x) –kx) – b
= b+ α(х) – b = α(х) → 0 при
х→ +∞.ЗАМЕЧАНИЕ.
Для случая горизонтальной асимптоты теорема формулируется так:
Для того, чтобы прямая y = b была асимптотой графика функции f(x) при х→ + ∞, необходимо и достаточно, чтобы