Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №8 Теория графов
Содержание
- 1. Тема №8 Теория графов
- 2. Основные понятияМногие задачи сводятся к рассмотрению совокупности
- 3. Понятие графаВ подобных случаях удобно рассматриваемые объекты
- 4. ОпределенияВершины и рёбра графа называются элементами графа, число
- 5. Типы графовОриентированный и неориентированный.Смешанный.Конечный и бесконечный.Полный граф.Мультиграф и псевдограф.Двудольный граф или биграф.
- 6. Пример формализации задачи с помощью графаЗадача Эйлера
- 7. Ориентированные графыЧасто связи между объектами характеризуются определенной
- 8. Конечный графЕсли множество вершин графа конечно, то
- 9. Мультиграф и псевдографГраф без петель и кратных
- 10. БиграфПростой граф, у которого любые две вершины
- 11. Смежность, инцидентность, степениДве вершины Vi и Vj
- 12. Инцидентность, степеньЕсли вершина Vi является началом
- 13. Теорема 1Для любого псевдографа сумма степеней всех
- 14. Матрицы графовЛюбой граф может быть задан матрицей
- 15. Матрица инцидентностиребравершиныпетляДля орграфа направление определяется знаком 1 или -1.
- 16. Изоморфизм графовГрафы в которых сохраняются отношения инцидентности
- 17. ЗАДАЧАТри дома с враждующими соседями и три
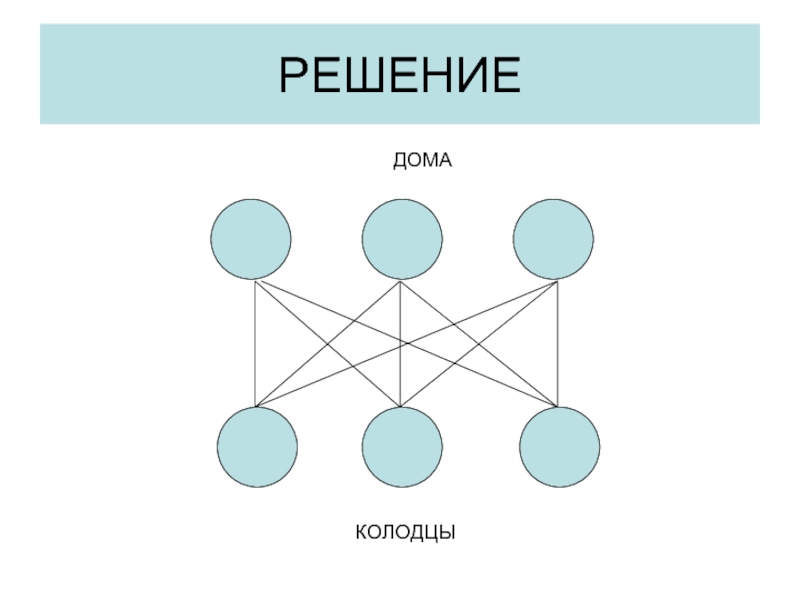
- 18. РЕШЕНИЕДОМАКОЛОДЦЫ
- 19. Особенность планарных графовУ планарных графов существует закономерность
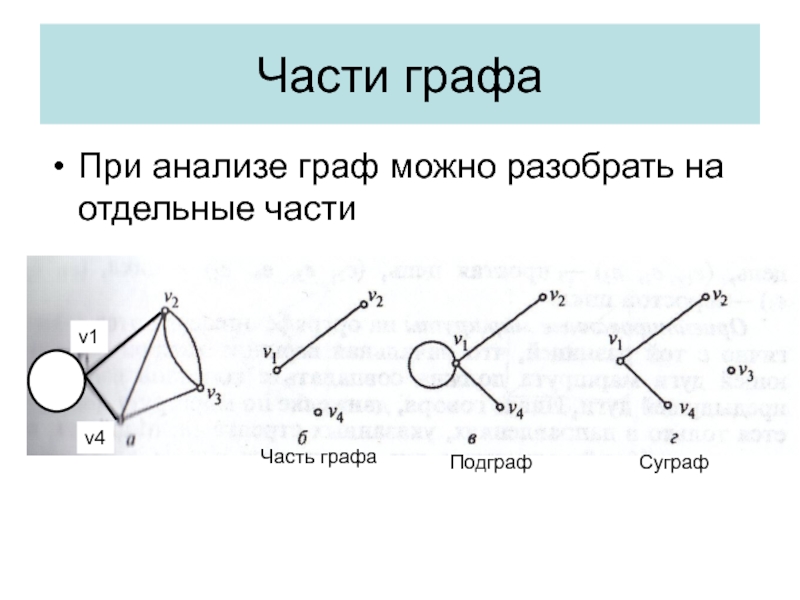
- 20. Части графаПри анализе граф можно разобрать на отдельные частиЧасть графаПодграфСуграфv1v4
- 21. Маршруты, цепи, циклы, путиПусть G неориентированный граф.
- 22. Коммутация абонентов через сеть транзитных узловСоединение узлов
- 23. Цепь и путьМаршрут, все ребра которого различны
- 24. СвязностьДве вершины графа называются связанными если существует
- 25. РасстояниеРасстоянием между вершинами неориентированного связного графа называют
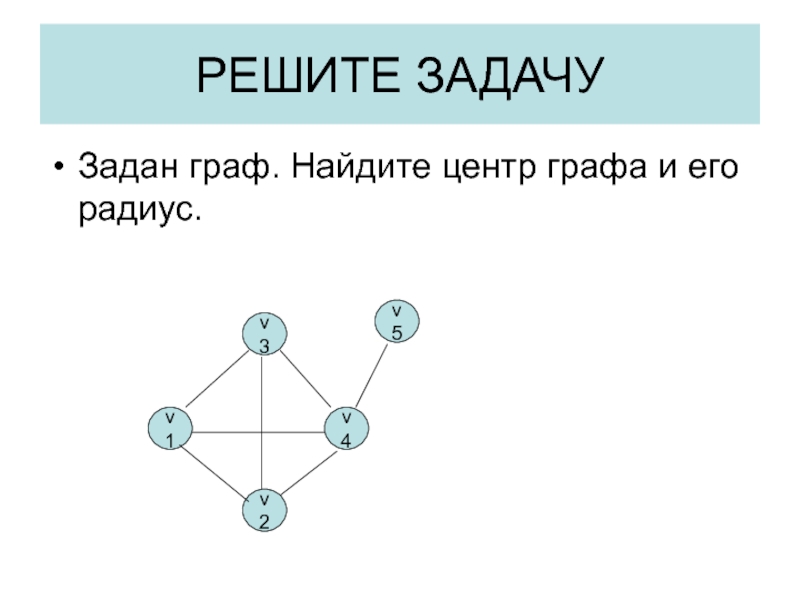
- 26. РЕШИТЕ ЗАДАЧУЗадан граф. Найдите центр графа и его радиус.v3v1v4v5v2
- 27. Эйлеровы циклы и цепиЭйлеров цикл – цикл
- 28. Теорема ЭйлераДля того чтобы неориентированный граф G
- 29. Понятие дерева и лесаНеориентированный связный граф не
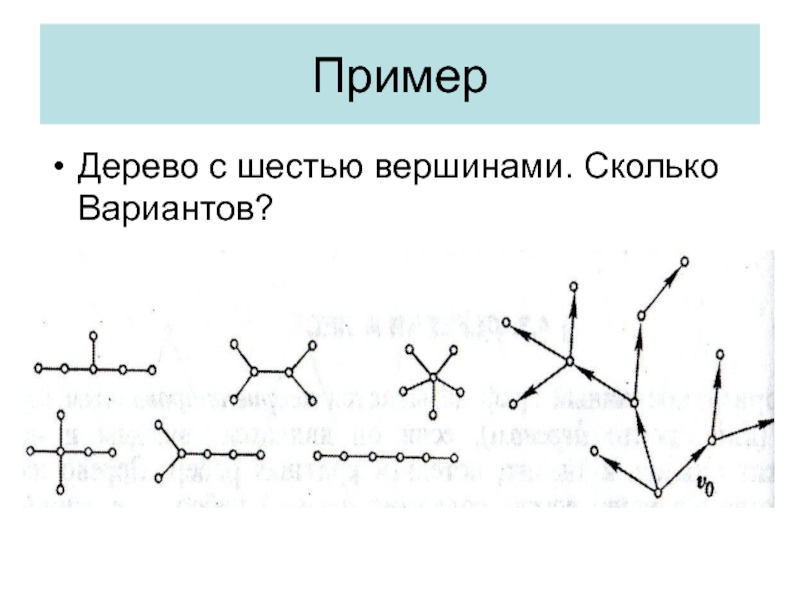
- 30. ПримерДерево с шестью вершинами. Сколько Вариантов?
- 31. Операции над графами1. Объединением графов G1(V1, E1) и G2(V2, E2) называется графG(V, E)
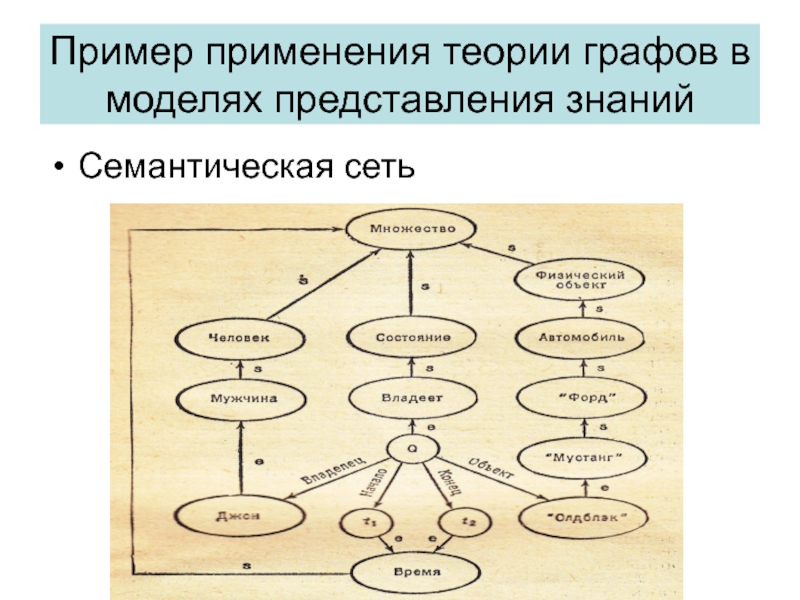
- 32. Пример применения теории графов в моделях представления знанийСемантическая сеть
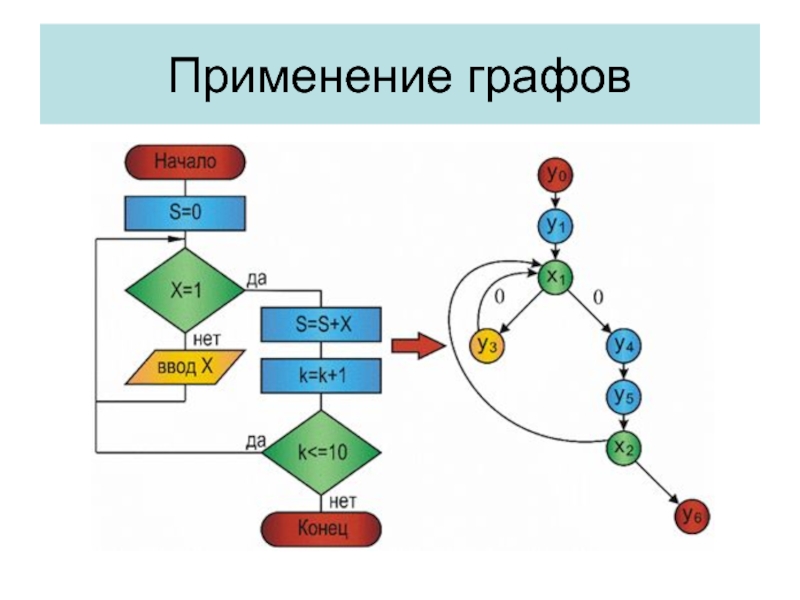
- 33. Применение графов
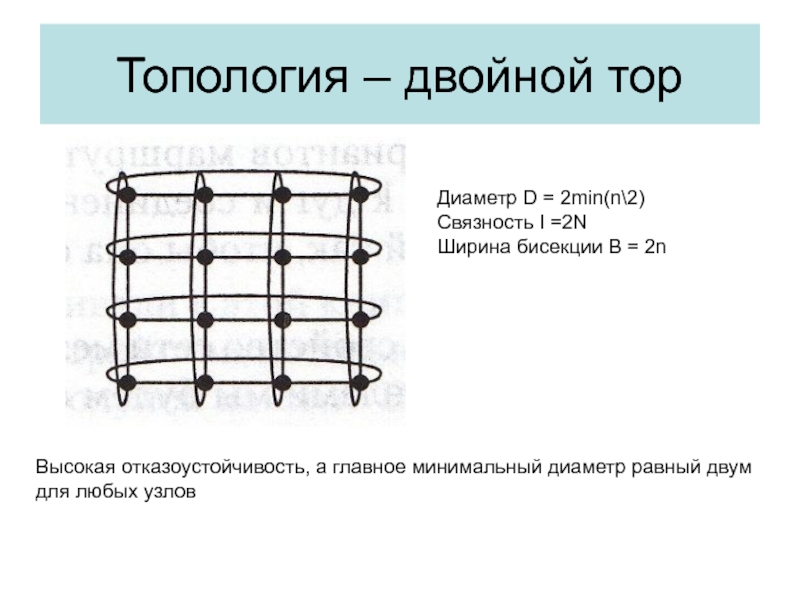
- 34. Топология – двойной торВысокая отказоустойчивость, а главное
- 35. Области применения теории графовБиологияХимия.Экономика.Транспорт.Логистика.
- 36. Скачать презентанцию
Основные понятияМногие задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними.НАПРИМЕР – Электрическая схема. - Карта дорог.
Слайды и текст этой презентации
Слайд 1Тема №8 Теория графов
Цель темы: рассмотреть основные понятия теории графов;
применение графов для формализации задач
Слайд 2Основные понятия
Многие задачи сводятся к рассмотрению совокупности объектов, существенные свойства
которых описываются связями между ними.
НАПРИМЕР – Электрическая схема.
- Карта дорог.- Описание конструкции.
- Работа цифрового
автомата.
Слайд 3Понятие графа
В подобных случаях удобно рассматриваемые объекты изображать точками, называемыми
вершинами, а связи между ними задавать линиями, называемыми ребрами.
Множество
вершин V, связи между которыми определены множеством ребер E, называют графом и обозначают G={V;E}
Слайд 4Определения
Вершины и рёбра графа называются элементами графа, число вершин в графе
— порядком, число рёбер — размером графа.
Вершины U и V называются концевыми вершинами (или просто концами) ребра e={U,V}
. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть e={U,U} .
Слайд 5Типы графов
Ориентированный и неориентированный.
Смешанный.
Конечный и бесконечный.
Полный граф.
Мультиграф и псевдограф.
Двудольный граф
или биграф.
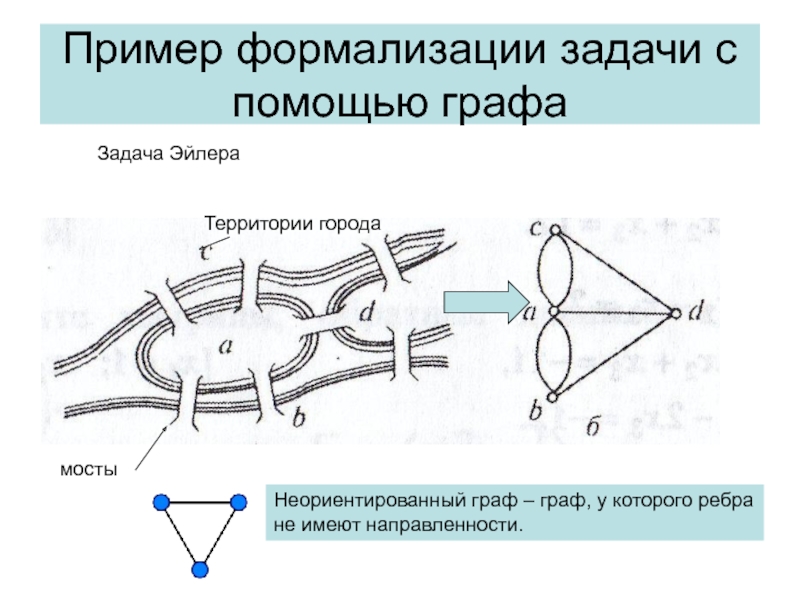
Слайд 6Пример формализации задачи с помощью графа
Задача Эйлера
Неориентированный граф –
граф, у которого ребра
не имеют направленности.
мосты
Территории города
Слайд 7Ориентированные графы
Часто связи между объектами характеризуются определенной ориентацией – направлением.
НАПРИМЕР
- течение тока, направление передачи сигнала, направление движения автомобилей, причинная
связь.Для указания направления ребро графа отмечается стрелкой и называется дугой, а граф с ориентированными ребрами называется орграфом.
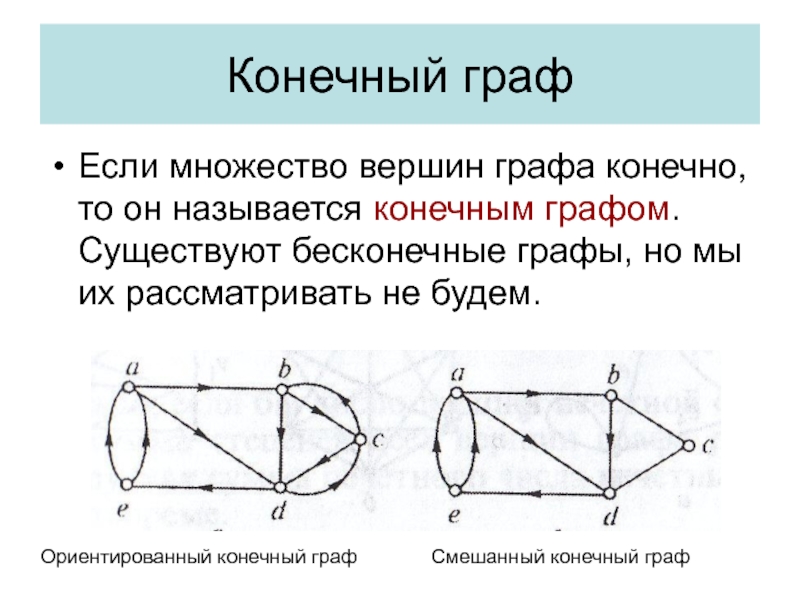
Слайд 8Конечный граф
Если множество вершин графа конечно, то он называется конечным
графом. Существуют бесконечные графы, но мы их рассматривать не будем.
Ориентированный
конечный графСмешанный конечный граф
Слайд 9Мультиграф и псевдограф
Граф без петель и кратных ребер называется обыкновенным
или простым графом.
Граф без петель, но с кратными ребрами называется
мультиграфом.Граф содержащий петли и кратные ребра называют псевдографом.
Слайд 10Биграф
Простой граф, у которого любые две вершины соединены называется полным.
Если
граф не имеет ребер, то все его вершины изолированы и
он называется пустым или нульграфом.Если множество вершин V простого графа допускает такое разбиение на два непересекающихся подмножества V1 и V2, что не существует ребер, соединяющие вершины одного и того же подмножества, то он называется биграфом.
Слайд 11Смежность, инцидентность, степени
Две вершины Vi и Vj графа G={V,E} называют
смежными. Если они являются вершинами ребра
Отношение смежности на множестве
вершин графа можно определить, представив каждое ребро как пару смежных вершин.Множество вершин V с определенным на нем отношением смежности
полностью определяет граф.
Слайд 12 Инцидентность, степень
Если вершина Vi является началом или концом ребра
Ek, то говорят что они инцидентны.
Инцидентность определяет отношение разнородных объектов
вершин и ребер графа.В орграфах различают положительную и отрицательную инцидентность.
Число ребер, инцидентных вершине называют степенью вершины. Петля учитывается дважды.
Слайд 13Теорема 1
Для любого псевдографа сумма степеней всех его вершин –
число четное равное удвоенному числу ребер графа.
ДОКАЗАТЕЛЬСТВО: Заключение этой теоремы
следует из того, что каждое ребро имеет два конца, а каждая петля учитывается два раза.СЛЕДСТВИЕ: В любом конечном графе число вершин нечетной степени четно.
Слайд 14Матрицы графов
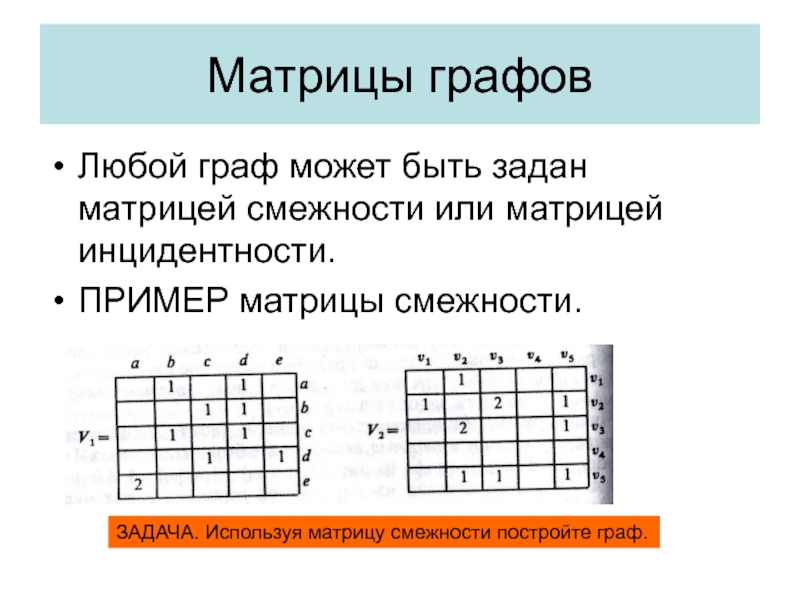
Любой граф может быть задан матрицей смежности или матрицей
инцидентности.
ПРИМЕР матрицы смежности.
ЗАДАЧА. Используя матрицу смежности постройте граф.
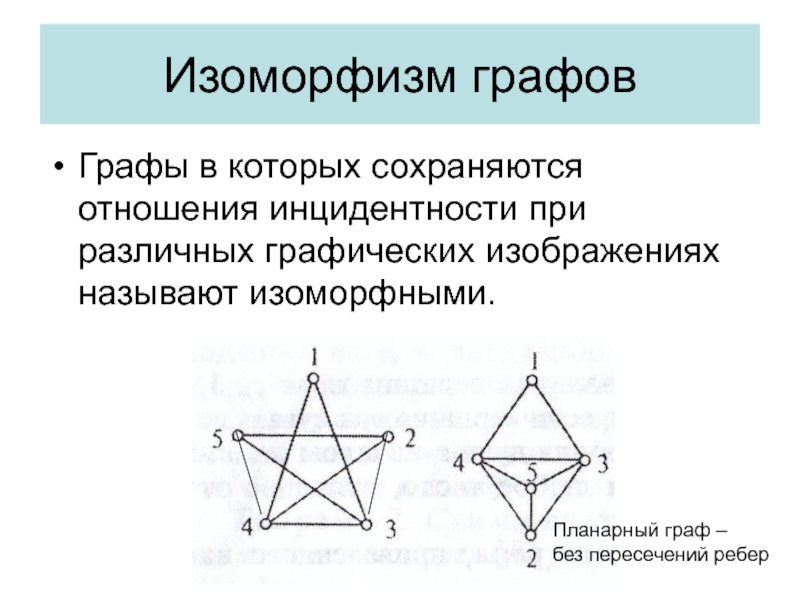
Слайд 16Изоморфизм графов
Графы в которых сохраняются отношения инцидентности при различных графических
изображениях называют изоморфными.
Планарный граф –
без пересечений ребер
Слайд 17ЗАДАЧА
Три дома с враждующими соседями и три колодца. ВОПРОС Можно
ли проложить дороги от домов к колодцам так, что бы
соседи идя к колодцу не встречались друг с другом?
Слайд 19Особенность планарных графов
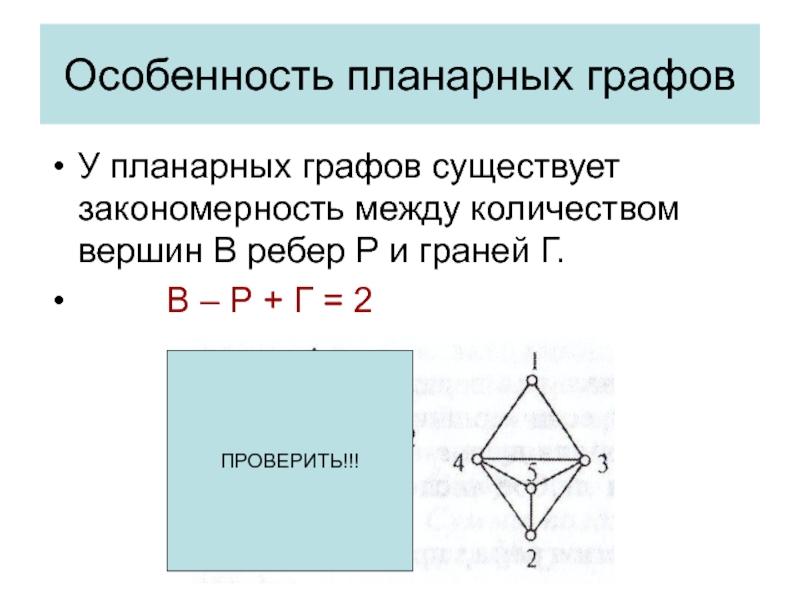
У планарных графов существует закономерность между количеством вершин
В ребер Р и граней Г.
В – Р + Г = 2ПРОВЕРИТЬ!!!
Слайд 21Маршруты, цепи, циклы, пути
Пусть G неориентированный граф. Маршрутом в G
называется такая последовательность ребер, в которой каждые два ребра имеют
инцидентную вершину. В маршруте одно и тоже ребро может встречаться несколько раз.В маршруте существует понятие начала и конца маршрута.
Слайд 22Коммутация абонентов через сеть транзитных узлов
Соединение узлов – это маршрут.
Узел
отправитель
Узел получатель.
Коммутация – соединение конечных узлов через сеть транзитных узлов.
ВОПРОС
СКОЛЬКО СУЩЕСТВУЕТ МАРШРУТОВ ИЗ УЗЛА 2 В УЗЕЛ 4;
Слайд 23Цепь и путь
Маршрут, все ребра которого различны называется цепью.
Маршрут у
которого различны все вершины называется простой цепью.
Замкнутая цепь называется циклом.
Понятие
ориентированный маршрут используется на орграфе.Число ребер маршрута называется длиной пути.
Слайд 24Связность
Две вершины графа называются связанными если существует маршрут соединяющий эти
вершины.
Граф, у которого любая пара вершин связана называется связным графом.
В противном случае граф называется несвязным.
Слайд 25Расстояние
Расстоянием между вершинами неориентированного связного графа называют минимальную длину простой
цепи связывающую эти вершины.
Центром графа называется вершина, от которой максимальное
расстояние до других вершин являлось бы минимальным.Максимальное расстояние от центра графа до его вершин называется радиусом графа.
Слайд 27Эйлеровы циклы и цепи
Эйлеров цикл – цикл графа, содержащий все
ребра графа.
Эйлеров граф - граф, имеющий эйлеров цикл (Эйлеров цикл
можно считать следом пера, вычерчивающего граф без отрыва от бумаги).ОПРЕДЕЛИТЕ ЭЛЕРОВ ЦИКЛ НА ГРАФАХ
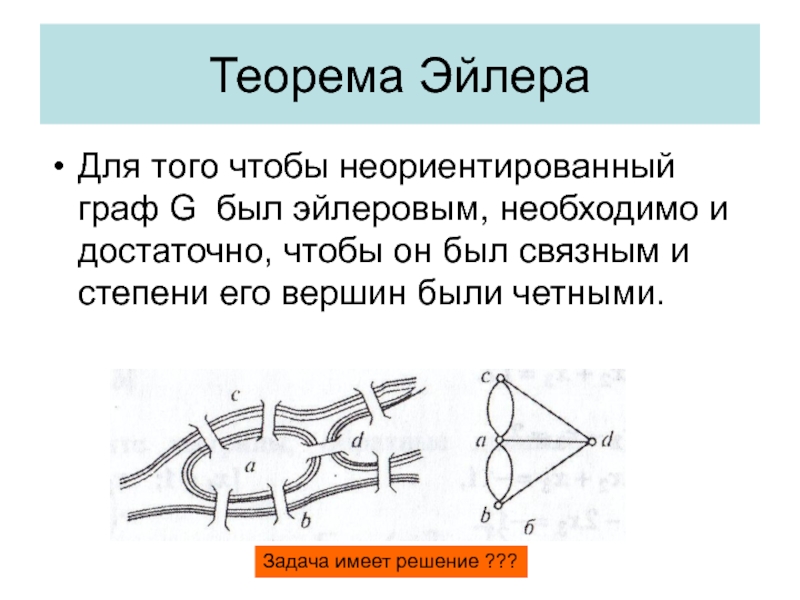
Слайд 28Теорема Эйлера
Для того чтобы неориентированный граф G был эйлеровым, необходимо
и достаточно, чтобы он был связным и степени его вершин
были четными.Задача имеет решение ???
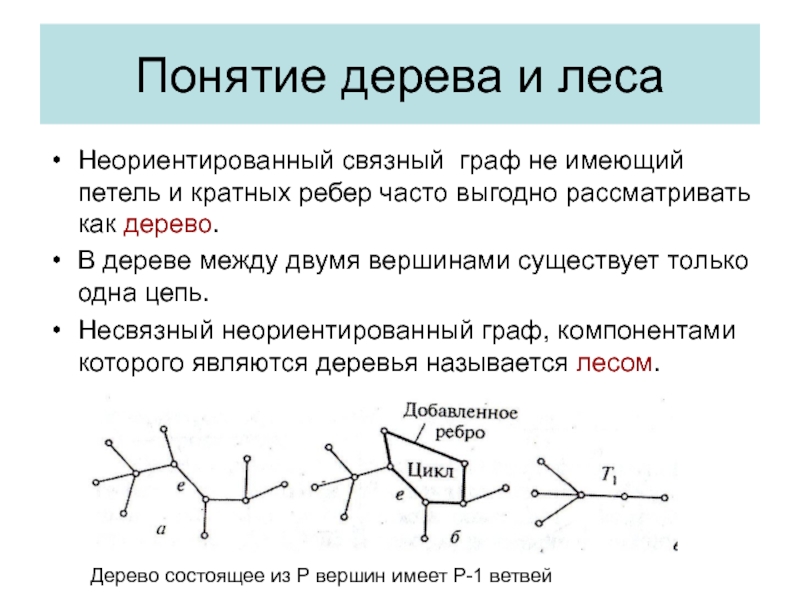
Слайд 29Понятие дерева и леса
Неориентированный связный граф не имеющий петель и
кратных ребер часто выгодно рассматривать как дерево.
В дереве между двумя
вершинами существует только одна цепь.Несвязный неориентированный граф, компонентами которого являются деревья называется лесом.
Дерево состоящее из Р вершин имеет Р-1 ветвей
Слайд 31Операции над графами
1. Объединением графов G1(V1, E1) и G2(V2, E2) называется граф
G(V, E) =
,
где V = , E =
.Аппарат теории множеств полностью применяется в теории графов
Слайд 34Топология – двойной тор
Высокая отказоустойчивость, а главное минимальный диаметр равный
двум
для любых узлов
Диаметр D = 2min(n\2)
Связность I =2N
Ширина бисекции B
= 2n
