Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Термодинамика и статистическая физика
Содержание
- 1. Термодинамика и статистическая физика
- 2. Лекция № 10Теплоёмкость многоатомных газов. 1.
- 3. Число независимых координат,
- 4. Числом степени свободы называется
- 5. Необходимо учитывать вращательное движение молекул
- 6. Многоатомная молекула может ещё и
- 7. Слайд 7
- 8. Двухатомная молекула, состоящая из жестко связанных атомов,
- 9. Трехатомная (многоатомная) моле-кула, состоящая из
- 10. У двухатомных молекул пять степеней
- 11. Слайд 11
- 12. При взаимных столкновениях молекул возможен обмен
- 13. Средняя энергия поступательного движения молекулы равна:
- 14. Больцман доказал, что, средняя энергия
- 15. В классической статистической физике выводится
- 16. Колебательная степень "обладает" вдвое
- 17. Итак, средняя энергия
- 18. У одноатомной молекулы i = 3,
- 19. На среднюю кинетическую энер-гию молекулы, имеющей
- 20. Теплоёмкости одноатомных и многоатомных газов Внутренняя энергия одного
- 21. То, что
- 22. Внутренняя энергия одного моля идеального газа c
- 23. Слайд 23
- 24. Для одного
- 25. для трех и более атомных молекул:
- 26. Слайд 26
- 27. В общем случае, для молярной массы газа
- 28. Для произвольного количества газов:
- 29. Слайд 29
- 30. Для одноатомных газов это
- 31. При увеличении температуры, когда Т >
- 32. Одна колебательная степень свободы несет
- 33. Слайд 33
- 34. Из качественной экспериментальной зависимости молярной теплоемкости
- 35. Это можно объяснить, предположив,
- 36. Расхождение теории и
- 37. к ней не применим закон равнораспределения энергии).
- 38. Лекция закончена !
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Лекция № 10
Теплоёмкость многоатомных газов.
1. Число степеней свободы.
Равномерное распределение средней кинетической энергии теплового движения по степеням свободы.
Классическая теория теплоёмкости многоатомных газов и её ограниченность. “Замороженные” степени свободы.Слайд 3
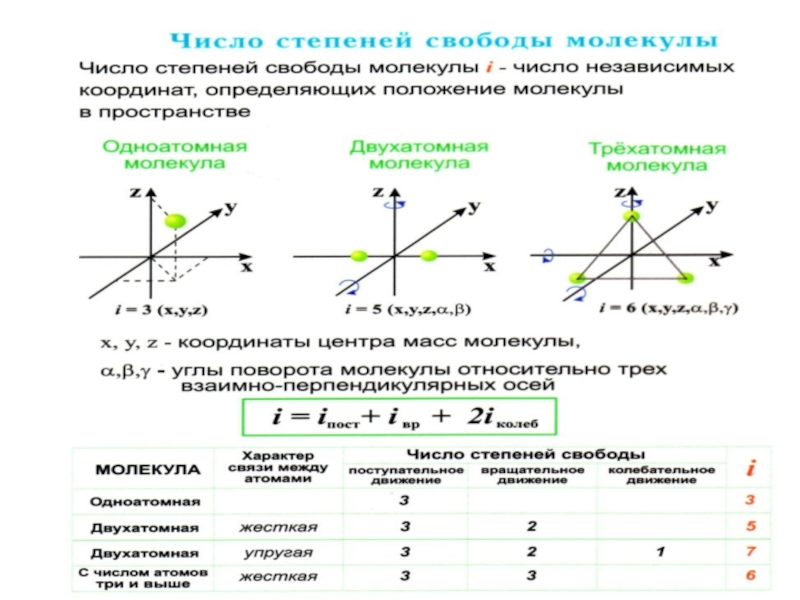
Число независимых координат, определяющих конфигурацию и
положение системы (атома или молекулы) в пространстве, называют числом степеней
свободы.Одноатомный газ – система невзаимодействующих материальных точек. Атом обладает
тремя поступатель-
ными степенями сво-
боды.
Слайд 4 Числом степени свободы называется число независимых переменных,
опреде-ляющих положение тела в пространстве и обозначается i
i = 3 Как видно, положение материальной точки (одноатомной молекулы) задаётся тремя координатами, поэтому она имеет три степени свободы: i = 3Слайд 5 Необходимо учитывать вращательное движение молекул и число степеней
свободы этих молекул.
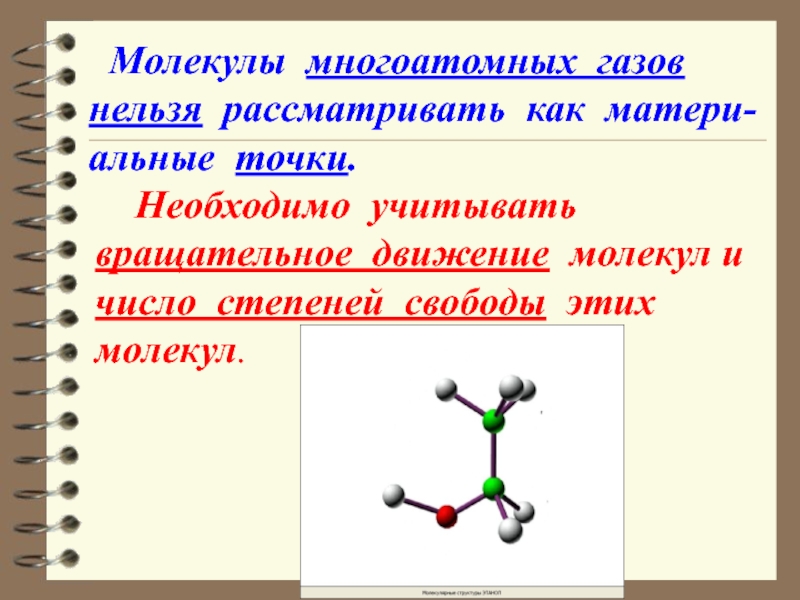
Молекулы многоатомных газов нельзя рассматривать как матери-альные
точки.Слайд 6 Многоатомная молекула может ещё и вращаться. Например, у
двухатомных молекул вращательное движение можно разложить на два независимых вращения,
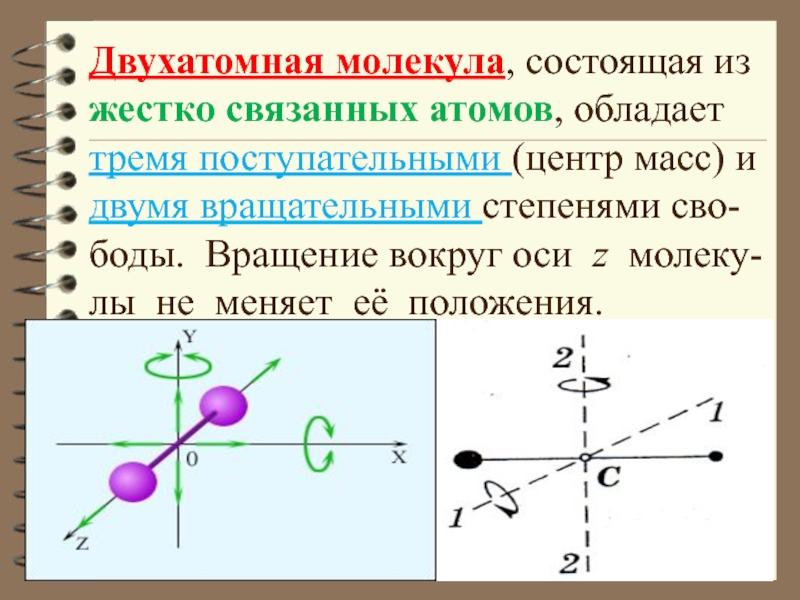
а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомных молекул вращение вокруг оси x не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю.Слайд 8Двухатомная молекула, состоящая из жестко связанных атомов, обладает
тремя поступательными
(центр масс) и двумя вращательными степенями сво-боды. Вращение вокруг оси
z молеку-лы не меняет её положения.Слайд 9 Трехатомная (многоатомная) моле-кула, состоящая из жестко связанных атомов,
обладает тремя поступатель-ными (центр масс) и тремя враща-тельными степенями свободы
i = 6.Если возможны колебания атомов, то добавляется колебательная степень свободы.
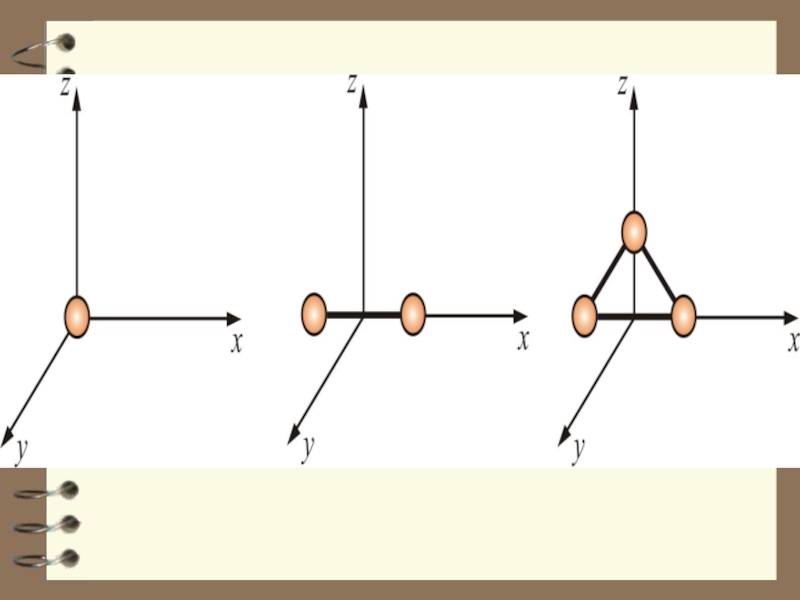
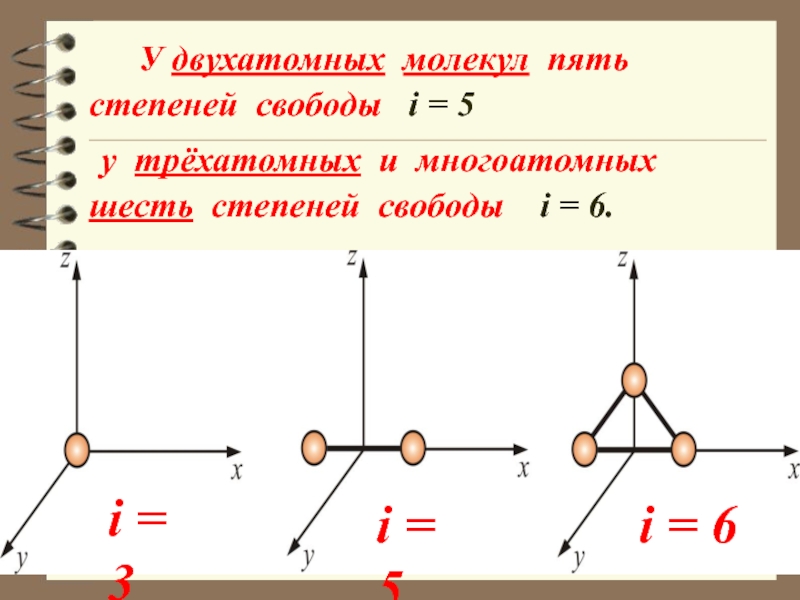
Слайд 10 У двухатомных молекул пять степеней свободы i
= 5
у трёхатомных и многоатомных шесть степеней свободы
i = 6.i = 6
i = 5
i = 3
Слайд 12 При взаимных столкновениях молекул возможен обмен их энергиями и превращение
энергии вращательного движения в энергию поступательного движения и обратно. Таким
путём установили равновесие между значениями средних энергий поступательного и вращательного движения молекул.Слайд 13 Средняя энергия поступательного движения молекулы равна:
Независимо от общего
числа степеней свободы молекул три степени свободы всегда поступательные. Ни
одна из поступательных степеней свободы не имеет преимущества перед другими,поэтому на каждую из них приходится в среднем одинаковая энергия, равная
1/3 значения Е, т.е.
Слайд 14 Больцман доказал, что, средняя энергия
приходящаяся на одну степень
свободы равна:
Закон о равномерном
распределении энергии по
степеням свободыСлайд 15 В классической статистической физике выводится закон Больцмана о
равномер-ном распределении энергии по степеням свободы молекул: для статистической системы,
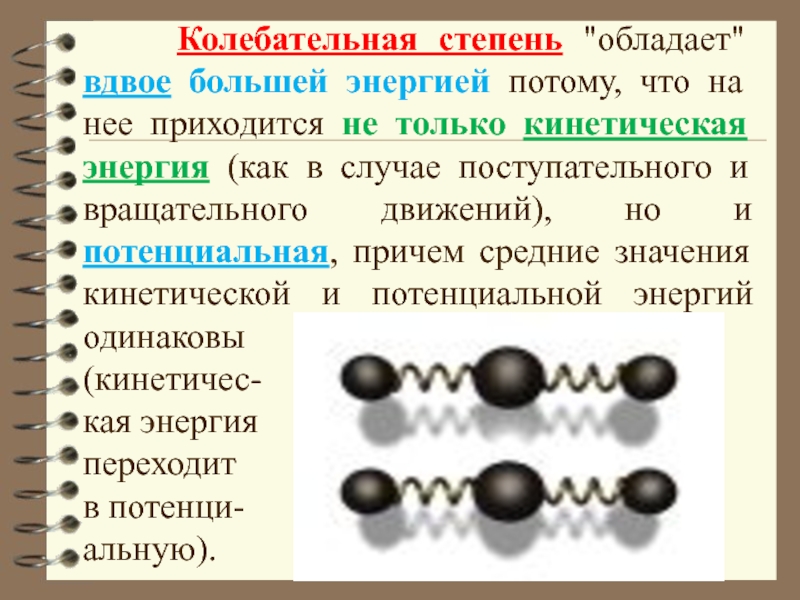
находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колеба-тельную степень свободы - в среднем энергия, равная .Слайд 16 Колебательная степень "обладает" вдвое большей энергией потому,
что на нее приходится не только кинетическая энергия (как в
случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы(кинетичес-
кая энергия
переходит
в потенци-
альную).
Слайд 18У одноатомной молекулы i = 3, тогда
для двухатомных молекул i = 5 для трёхатомных молекул i = 6
Слайд 19 На среднюю кинетическую энер-гию молекулы, имеющей i-степеней свободы приходится
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы. Здесь i = iпост + iвращ + 2iкол
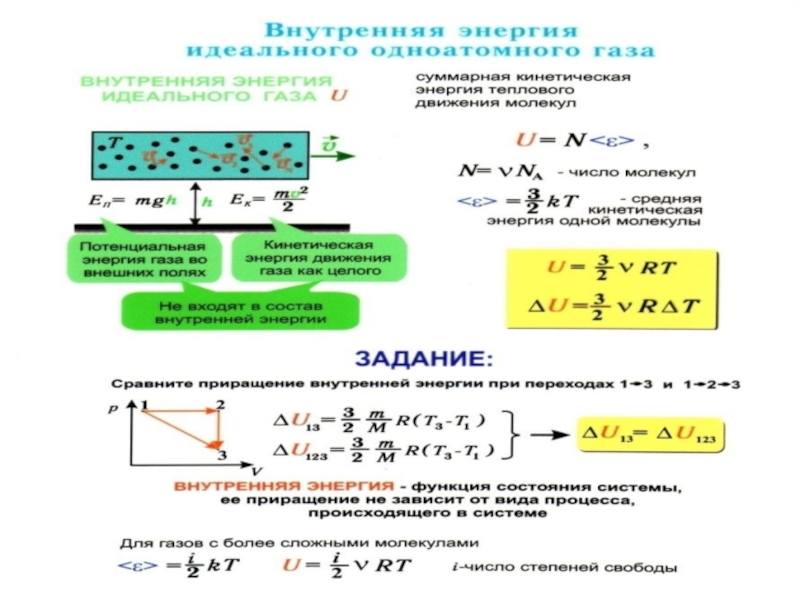
Слайд 20Теплоёмкости одноатомных и многоатомных газов
Внутренняя энергия одного моля одноатомного идеального
газа равна
Слайд 22 Внутренняя энергия одного моля идеального газа c i степенями свободы
равна:
молярная теплоемкость при постоянном объеме СV – величина постоянная, от температуры не зависит.
Слайд 24
Для одного моля идеального
газа:
Постоянная адиабаты (коэффициент Пуассона) для идеального
газа:
Для одноатомного идеаль-
ного газа (i = 3):
Слайд 28 Для произвольного количества газов:
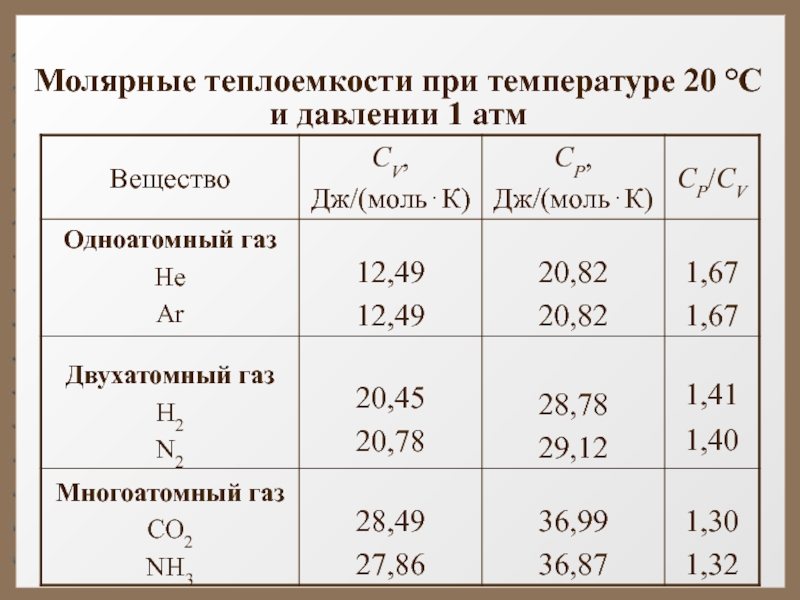
Из теории также следует, что СV не зависит от температуры (рисунок).
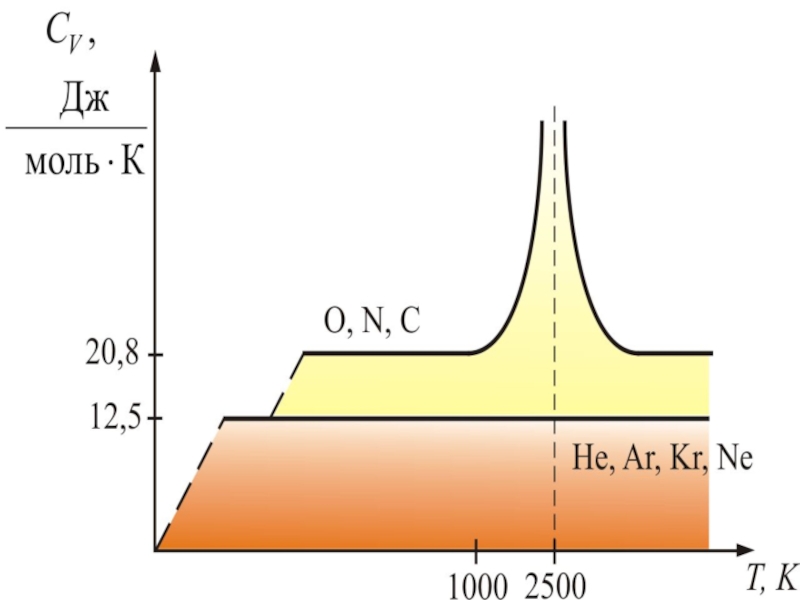
Слайд 30 Для одноатомных газов это выполняется в очень
широких пределах, а для двухатомных газов только в интервале от
100 1000 К. Отличие связано с проявлением квантовых законов. При низких температурах вращательное движение как бы «заморожено» и двухатомные молекулы движутся поступательно, как одноатомные и равны их теплоёмкости.Слайд 31 При увеличении температуры, когда
Т > 1000 К, начинают
сказываться колебания атомов молекулы вдоль оси z (атомы в молекуле
связаны не жёстко, а как бы на пружине).Слайд 32Одна колебательная степень свободы несет энергии,
так как при этом есть и кине-тическая и потенциальная энергия,
то есть появляется шестая степень свободы – коле-бательная. При температуре равной 2500 К, молекулы диссоциируют. На диссоциацию молекул тратится энергия раз в десять пре-вышающая среднюю энергию поступатель-ного движения. Это объясняет сравнитель-но низкую температуру пламени. Кроме то-го, атом – сложная система, и при высоких температурах начинает сказываться дви-жение электронов внутри него.Слайд 34Из качественной экспериментальной зависимости молярной теплоемкости водорода
(см. рис.), следует, что зависит от температуры:
при
низкой температуре (около 50 К) - при комнатной -
(вместо расчетной !)
и при очень высокой -
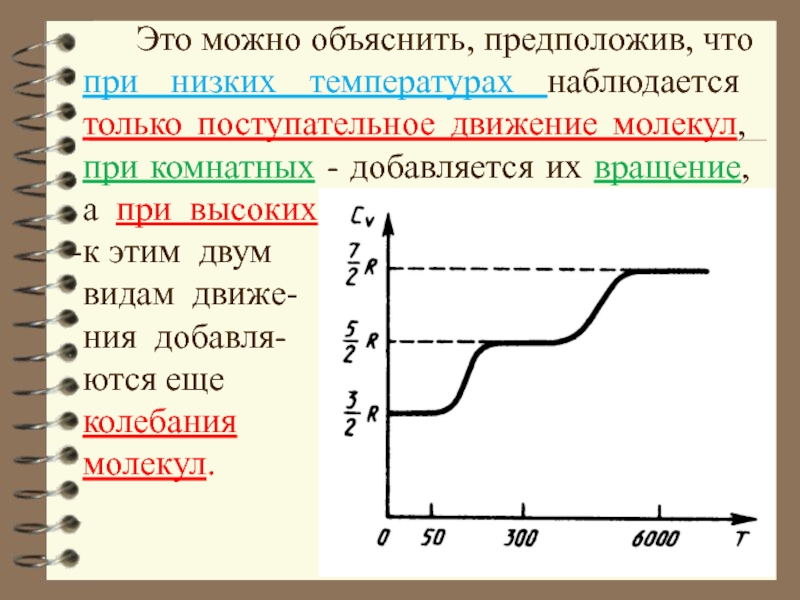
Слайд 35 Это можно объяснить, предположив, что при низких
температурах наблюдается только поступательное движение молекул, при комнатных - добавляется
их вращение, а при высокихк этим двум
видам движе-
ния добавля-
ются еще
колебания
молекул.
Слайд 36 Расхождение теории и эксперимента нетрудно объяснить.
Дело в том, что при вычислении теплоемкости надо учитывать квантование
энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоемкость (соответствующая степень свободы "замораживается"Слайд 37к ней не применим закон равнораспределения энергии). Этим объясняется, что
теплоемкость моля двухатомного газа – водорода - при комнатной температуре
равнавместо .
Аналогично можно объяснить уменьшение теплоемкости при низкой температуре ("замораживаются" вращательные степени свободы) и увеличение при высокой ("возбуждаются" колебательные степени свободы).