Тригонометрическая и показательная формы комплексного числа: z = А(cosφ +

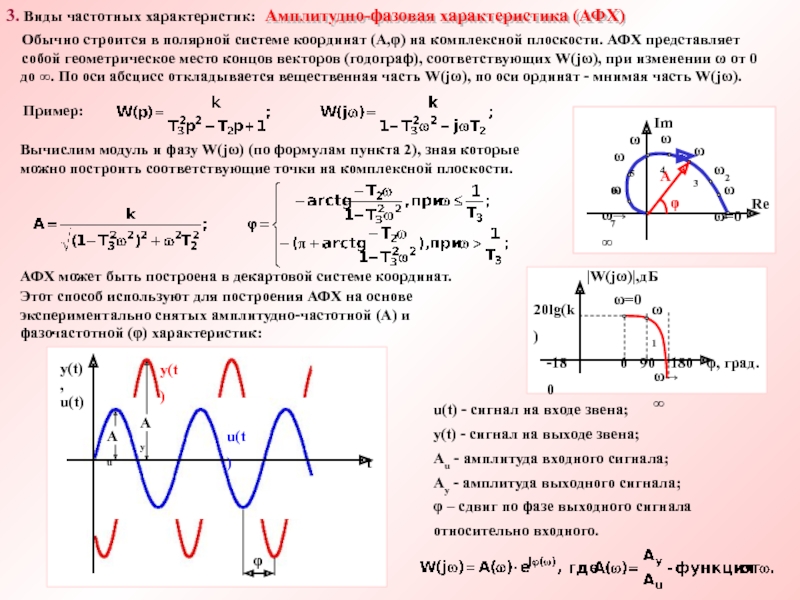
x + jy,

Im(z)

Re(z)

x

y

A

φ

ІV

ІІІ

ІІ

І

z=x+jy

Рис. Графическое представление комплексного числа

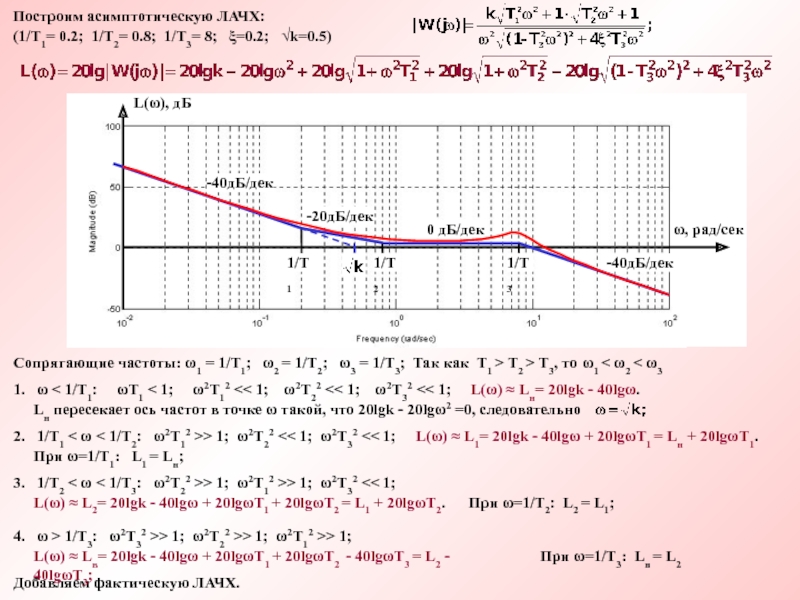
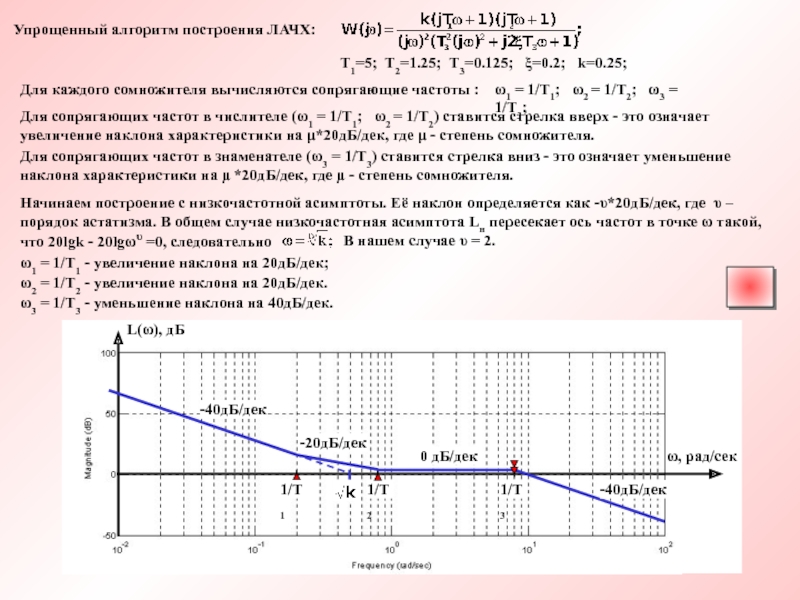
Из соотношения: tgφ = y/x, получаем φ = arctg(y/x) + πn, n - целое; n выбирается с учетом того, что радиус-вектор точки z лежит в интервале (-π/2+πn, π/2+πn), например I, IV: n = 0; II, III: n =  1 (знак зависит от того, в каком направлении от нуля мы отсчитываем угол)

Встречаются примеры, в которых х=0, тогда приходит-ся вводить дополнительные условия (это особенно не-удобно при алгоритмизации расчета). В этом случае ис-пользуют следующее соотношение sinφ = y/A, тогда φ = (-1)n arcsin(y/A) + πn, n - целое (выбирается аналогично случаю с арктангенсом).

Y(p)/U(p), где U(p), Y(p) - изображения по Лапласу входной и

2. Комплексный передаточный коэффициент:

где

- модуль W(jω),

- фаза W(jω),

здесь Аi, φi - модуль и фаза i-го сомножителя в числителе или знаменателе.

При построении частотных характеристик не рекомендуется раскладывать W(jω) на реальную и мнимую части, потому что при этом степень знаменателя увеличивается в два раза, что усложняет дальнейшую работу (удобнее пользоваться формулами для модуля и фазы).

Например:

используют для построения АФХ на основе экспериментально снятых амплитудно-частотной (А)

90

180

20lg(k)

ω=0

ω1

ω

Аu

Аy

φ

y(t)

u(t)

t

u(t) - сигнал на входе звена; y(t) - сигнал на выходе звена; Au - амплитуда входного сигнала; Ay - амплитуда выходного сигнала; φ – сдвиг по фазе выходного сигнала относительно входного.

Вычислим модуль и фазу W(jω) (по формулам пункта 2), зная которые можно построить соответствующие точки на комплексной плоскости.

A

ω1

ω3

ω4

ω2

ω5

ω

ω=0

ω7

ω6

φ

y(t),
u(t)

3. Виды частотных характеристик:

Амплитудно-фазовая характеристика (АФХ)

Обычно строится в полярной системе координат (А,φ) на комплексной плоскости. АФХ представляет собой геометрическое место концов векторов (годограф), соответствующих W(jω), при изменении ω от 0

до . По оси абсцисс откладывается вещественная часть W(jω), по оси ординат - мнимая часть W(jω).

Пример:

а около отметок указывается значение частоты (ω) в рад/сек.
0
1
2
-1
-2
20
-20
0
L(ω), дБ
lgω
0.01
0.1
1
10
100
ω,

По оси ординат откладывается модуль в децибелах. L(ω) = 20lg|W(jω)|. Децибел является единицей логарифмической относительной величины.

Изменение |W(jω)| в 10 раз соответствует изменению L(ω) на 20 дБ (в 100 раз - на 40 дБ; в 1000 раз - на 60 дБ ).

Амплитудно-частотная (АЧХ) и фазочастотная (ФЧХ) характеристики

АЧХ: А(ω) = |W(jω)| - характеризует изменение амплитуды А при изменении частоты ω.

ФЧХ: φ(ω) = Arg(W(jω)) - дает представление о фазовом сдвиге выходных колебаний относительно

Так как изменение частотных характеристик реальных динамических звеньев, объектов и систем происходит в большом диапазоне частот (отношение ωmax /ωmin может быть порядка 103  104), а также в большом диапазоне изменения модуля |W(jω)|, то удобно использовать логарифмические частотные характеристики (ЛЧХ).

входных.

1

0

2

3

4

5

6

7

8

9

10

1

lgω

ω

0,301

0,477

0,602

0,699

0,778

0,845

0,903

0,954

одной декадой, отрезок, соответствующий изменению частоты в 2 раза -

-1

0

1

0.1

10

1

100

2

2

0.2

30

5

60

Декада определяется выражением: lg10ω - lgω = lg10 = 1 (Одна декада);

Октава: lg2ω - lgω = lg2 = 0.301 (0.301 от декады).

lgω

ω

Изменению частоты в одно и тоже число раз соответствует перемещение по оси абсцисс (в логарифмическом масштабе) на один и тот же интервал.

Для построения ЛФЧХ используется та же ось частот, а по оси ординат откладывается фаза в градусах или радианах в линейном масштабе.

I. Отдельно строятся φi (составляющие фазы φ), которые потом геометрически складываются;

II. Построение по точкам (используется формула φ = Arg(W(jω))).

ЛФЧХ строятся одним из 2 способов:

Логарифмические частотные характеристики представляют собой комплект из двух характеристик: ЛАЧХ и ЛФЧХ.

Т = 5:
ω = 1/T

ω2T2

ω=1/T

2. ω > 1/T: ωT > 1; ω2T2 >> 1; L(ω)  Lв= -20lgωT - прямая с наклоном - 20 дБ/дек,

-20 дБ/дек

Построим асимптотическую ЛАЧХ:

Действительная ЛАЧХ отличается от асимптотической.

Наибольшее отклонение будет в точке ω = 1/Т, и оно равно примерно 3дБ:

ω = 1/T: Lн = Lв.

3дБ

0 дБ/дек

k=0.25:
2)
ЛФЧХ
ЛАЧХ

1; ω2T12

(1/Т1= 0.2; 1/T2= 0.8; 1/T3= 8; ξ=0.2; k=0.5)

Построим асимптотическую ЛАЧХ:

Добавляем фактическую ЛАЧХ.

ω, рад/сек

Сопрягающие частоты: ω1 = 1/T1; ω2 = 1/T2; ω3 = 1/T3; Так как Т1 > Т2 > Т3, то ω1 < ω2 < ω3

Lн пересекает ось частот в точке ω такой, что 20lgk - 20lgω2 =0, следовательно

2. 1/Т1 < ω < 1/T2: ω2T12 >> 1; ω2T22 << 1; ω2T32 << 1; L(ω)  L1= 20lgk - 40lgω + 20lgωT1 = Lн + 20lgωT1.

При ω=1/Т1: L1 = Lн;

3. 1/Т2 < ω < 1/T3: ω2T22 >> 1; ω2T12 >> 1; ω2T32 << 1;

L(ω)  L2= 20lgk - 40lgω + 20lgωT1 + 20lgωT2 = L1 + 20lgωT2. При ω=1/Т2: L2 = L1;

4. ω > 1/T3: ω2T32 >> 1; ω2T22 >> 1; ω2T12 >> 1;

При ω=1/Т3: Lв = L2

L(ω)  Lв= 20lgk - 40lgω + 20lgωT1 + 20lgωT2 - 40lgωT3 = L2 - 40lgωT3;

1/T1

-40дБ/дек

1/T2

1/T3

-20дБ/дек

-40дБ/дек

0 дБ/дек

сопрягающие частоты :
ω1 = 1/T1; ω2 = 1/T2;

Т1=5; T2=1.25; T3=0.125; ξ=0.2; k=0.25;

Для сопрягающих частот в числителе (ω1 = 1/T1; ω2 = 1/T2) ставится стрелка вверх - это означает увеличение наклона характеристики на μ*20дБ/дек, где μ - степень сомножителя.

Для сопрягающих частот в знаменателе (ω3 = 1/T3) ставится стрелка вниз - это означает уменьшение наклона характеристики на μ *20дБ/дек, где μ - степень сомножителя.

ω1 = 1/T1 - увеличение наклона на 20дБ/дек;

ω2 = 1/T2 - увеличение наклона на 20дБ/дек.

ω3 = 1/T3 - уменьшение наклона на 40дБ/дек.

Начинаем построение с низкочастотной асимптоты. Её наклон определяется как -υ*20дБ/дек, где υ – порядок астатизма. В общем случае низкочастотная асимптота Lн пересекает ось частот в точке ω такой, что 20lgk - 20lgωυ =0, следовательно

В нашем случае υ = 2.