Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Углы и стороны треугольника
Содержание
- 1. Углы и стороны треугольника
- 2. Данные слайды используются при рассмотрении теоретического материала по теме: соотношения между сторонами и углами треугольника.
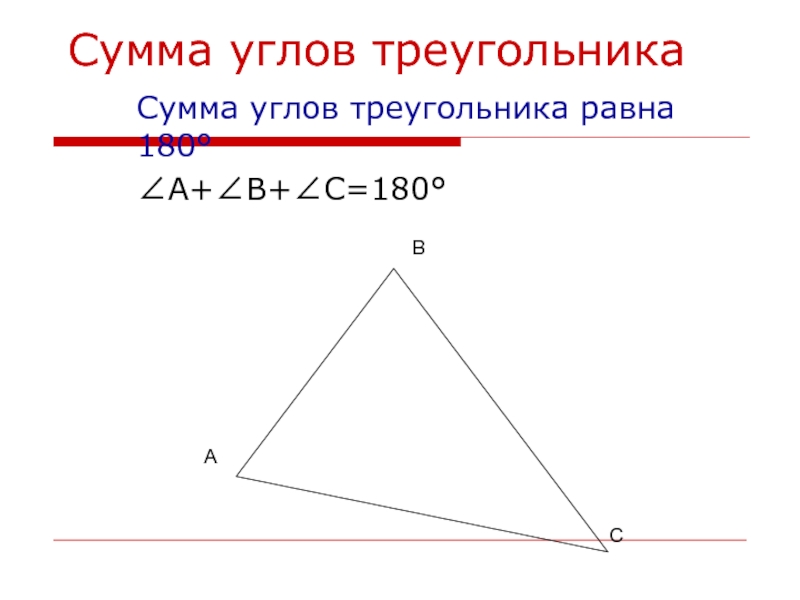
- 3. Сумма углов треугольникаСумма углов треугольника равна 180°∠А+∠В+∠С=180°АВС
- 4. Дано: треугольник АВСДоказать: ∠А+∠В+∠С=180°Доказательство: а
- 5. ВНЕШНИЙ УГОЛУгол смежный с каким-нибудь углом треугольника называется внешним углом треугольника __ ∠4АВС4123Д
- 6. Свойство внешнего углаВнешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: ∠4=∠1+∠2АВС4123
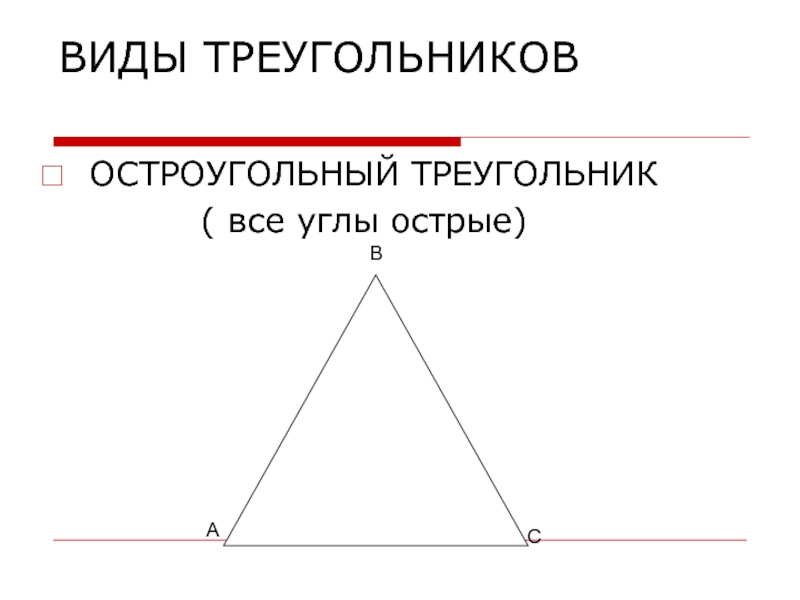
- 7. ВИДЫ ТРЕУГОЛЬНИКОВОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ( все углы острые)АВС
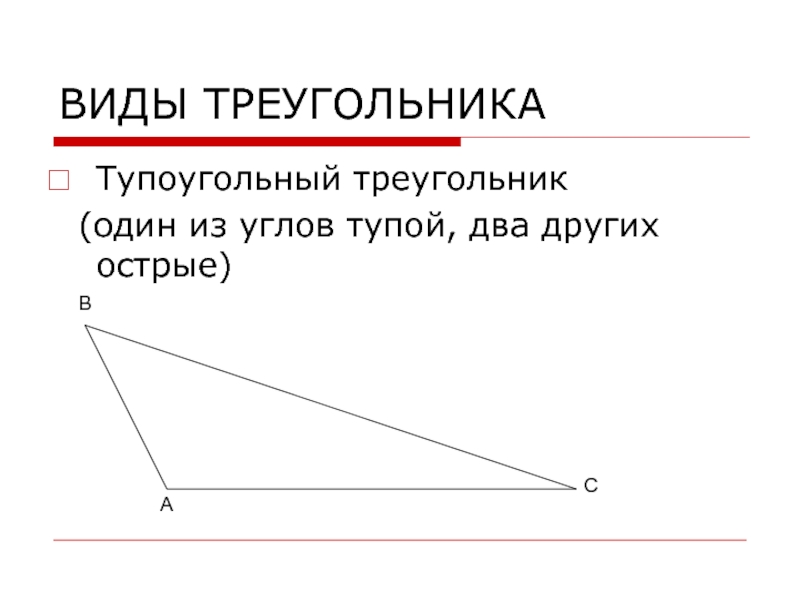
- 8. ВИДЫ ТРЕУГОЛЬНИКАТупоугольный треугольник (один из углов тупой, два других острые)АВС
- 9. ВИДЫ ТРЕУГОЛЬНИКАПрямоугольный треугольник(один из углов прямой, а
- 10. Соотношения между сторонами и углами треугольникаВ треугольнике:
- 11. СЛЕДСТВИЯ1. В прямоугольном треугольнике гипотенуза больше катета.Если
- 12. НЕРАВЕНСТВО ТРЕУГОЛЬНИКАТеорема: Каждая сторона треугольника меньше суммы
- 13. СЛЕДСТВИЕДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК А,В И С,
- 14. ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ(свойства)1. Сумма двух острых углов прямоугольного
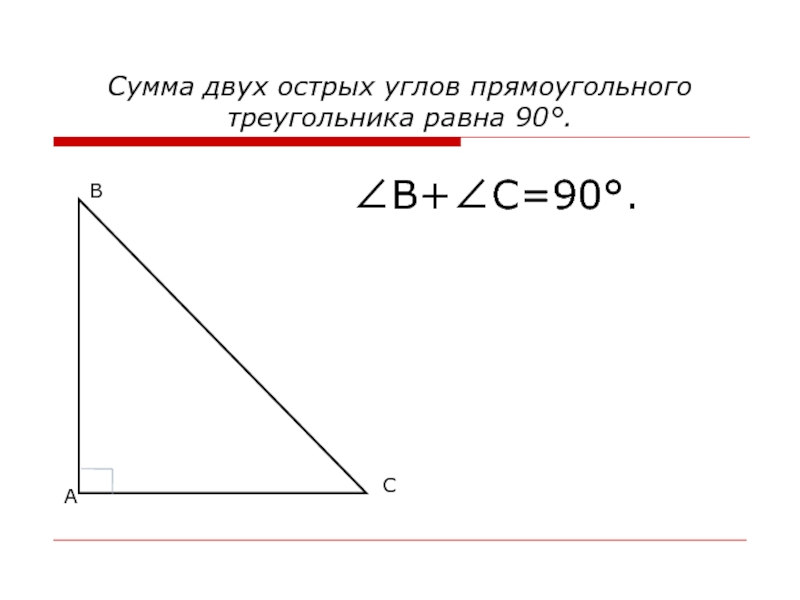
- 15. Сумма двух острых углов прямоугольного треугольника равна 90°.ВАС∠В+∠С=90°.
- 16. Катет прямоугольного треугольника, лежащего против угла в
- 17. Если катет прямоугольного треугольника равен половине гипотенузы,
- 18. Признаки равенства прямоугольных треугольников.Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- 19. Признаки равенства прямоугольных треугольников.Если катет и прилежащий
- 20. Признаки равенства прямоугольных треугольников.Если гипотенуза и острый
- 21. Признаки равенства прямоугольных треугольниковЕсли гипотенуза и катет
- 22. Скачать презентанцию
Данные слайды используются при рассмотрении теоретического материала по теме: соотношения между сторонами и углами треугольника.
Слайды и текст этой презентации
Слайд 1«Сумма углов треугольника»
Разработчик:
учитель математики МОУ СОШ № 2 города
Радужный
Мишурова Любовь Александра
Слайд 2Данные слайды используются при рассмотрении теоретического материала по теме: соотношения
между сторонами и углами треугольника.
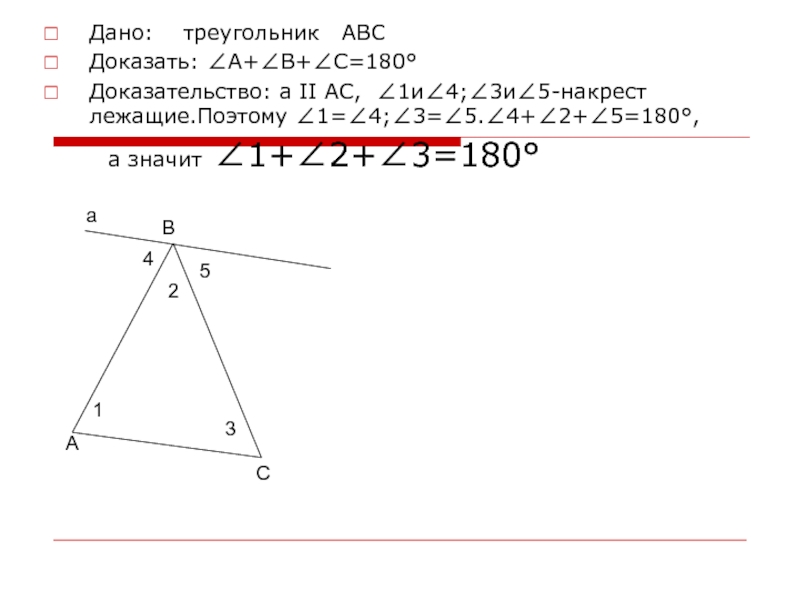
Слайд 4Дано: треугольник АВС
Доказать: ∠А+∠В+∠С=180°
Доказательство: а II АС, ∠1и∠4;∠3и∠5-накрест
лежащие.Поэтому ∠1=∠4;∠3=∠5.∠4+∠2+∠5=180°,
а значит ∠1+∠2+∠3=180°
А
В
С
а
1
3
2
4
5
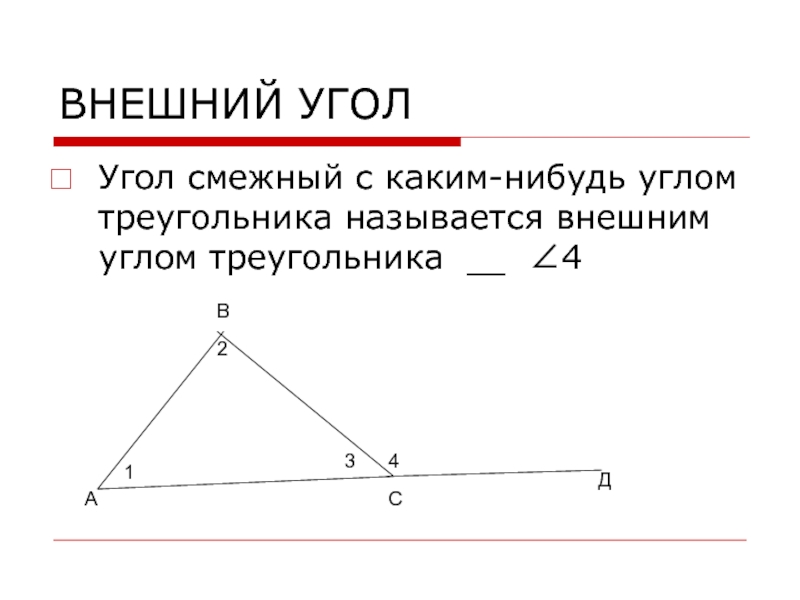
Слайд 5ВНЕШНИЙ УГОЛ
Угол смежный с каким-нибудь углом треугольника называется внешним углом
треугольника __ ∠4
А
В
С
4
1
2
3
Д
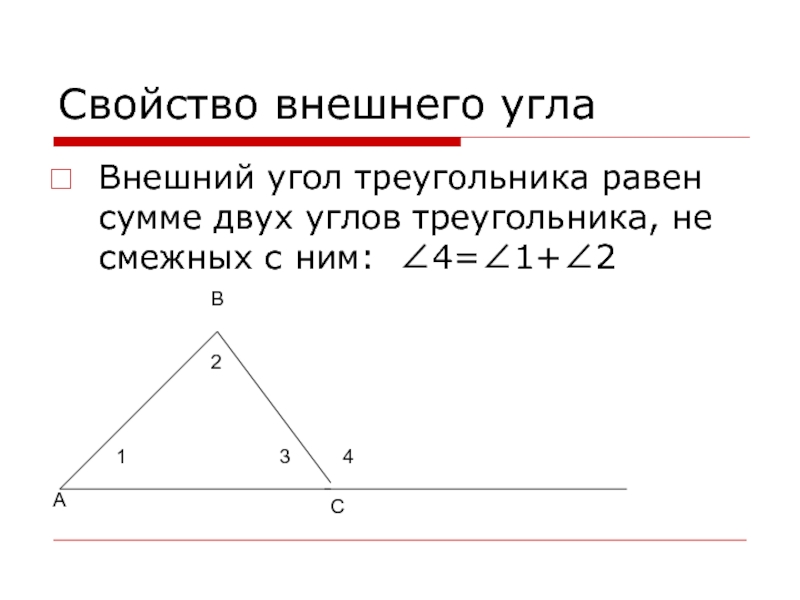
Слайд 6Свойство внешнего угла
Внешний угол треугольника равен сумме двух углов треугольника,
не смежных с ним: ∠4=∠1+∠2
А
В
С
4
1
2
3
Слайд 9ВИДЫ ТРЕУГОЛЬНИКА
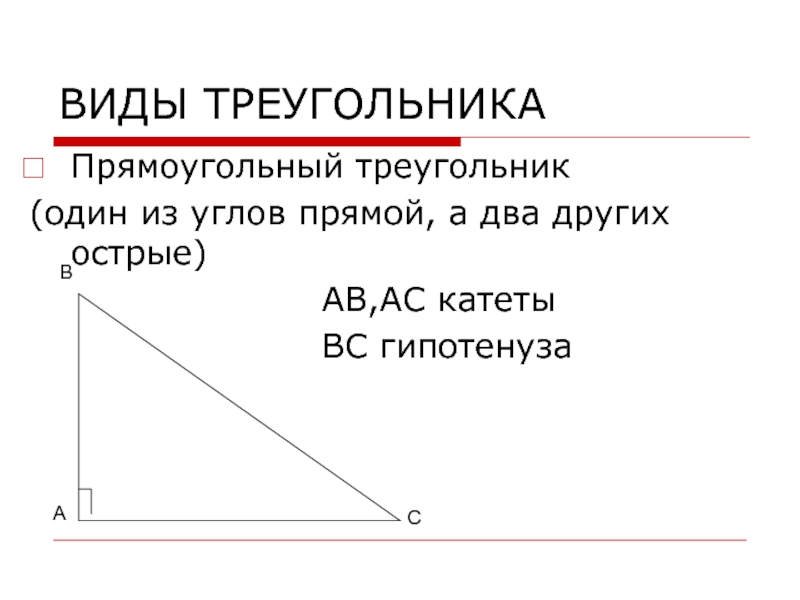
Прямоугольный треугольник
(один из углов прямой, а два других острые)
АВ,АС катеты
ВС гипотенуза
А
В
С
Слайд 10Соотношения между сторонами и углами треугольника
В треугольнике: 1) против большей
стороны лежит больший угол;
2) обратно, против большего угла
лежит большая сторона.1)АС большая сторона, значит ∠В больший.
2)∠В большей, значит АС большая сторона.
А
С
В
Слайд 11СЛЕДСТВИЯ
1. В прямоугольном треугольнике гипотенуза больше катета.
Если в треугольнике два
угла равны, то треугольник равнобедренный( признак равнобедренного треугольника).
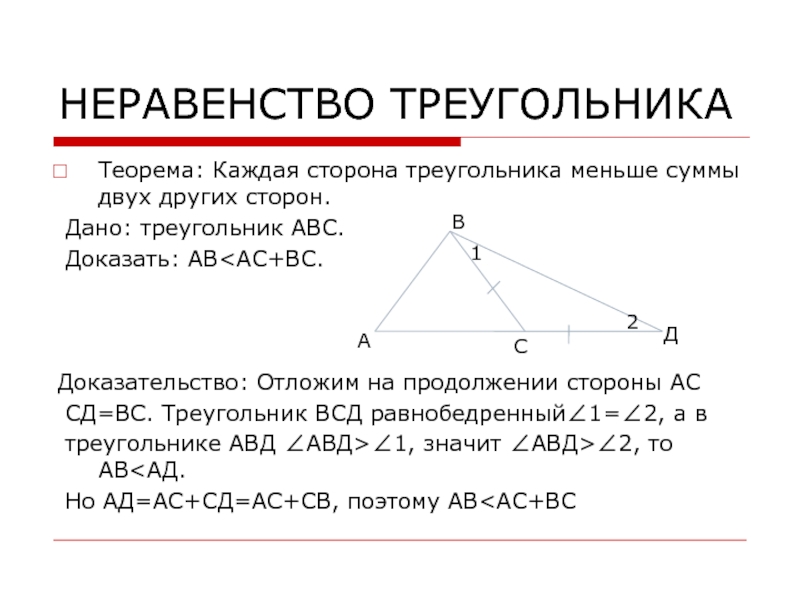
Слайд 12НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Теорема: Каждая сторона треугольника меньше суммы двух других сторон.
Дано: треугольник АВС.
Доказать: АВ
АССД=ВС. Треугольник ВСД равнобедренный∠1=∠2, а в
треугольнике АВД ∠АВД>∠1, значит ∠АВД>∠2, то АВ<АД.
Но АД=АС+СД=АС+СВ, поэтому АВ<АС+ВС
2
1
В
А
С
Д
Слайд 13СЛЕДСТВИЕ
ДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК А,В И С, не лежащих на
одной прямой, справедливы неравенства:
АВ< АС+ВС;
АС< АВ+ВС;
ВС< ВА+АС.
Слайд 14ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ(свойства)
1. Сумма двух острых углов прямоугольного треугольника равна 90°.
2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен
половине гипотенузы.3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Слайд 16Катет прямоугольного треугольника, лежащего против угла в 30°, равен половине
гипотенузы.
Рассмотрим треугольник АВС, где ∠А=90°, ∠В=30° и ∠С=60°. Док-ть, что
АС=½ВС.Рассмотрим треугольник АВС, где ∠А=90°, ∠В=30° и ∠С=60°. Докажем, что АС=½ВС.
Приложим к треугольнику АВС равный ему
треугольник АВД. Получим
треугольник ВСД, ∠В=∠Д=60°,
поэтому ДС = ВС, но АС= ½ ДС,
значит АС = ½ ВС.
6
В
Д
С
А
30°
30°
60°
60°
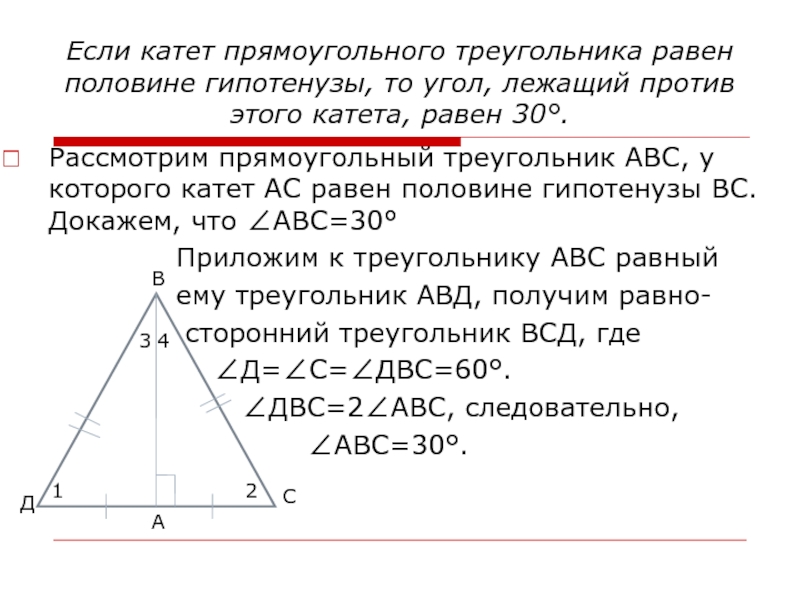
Слайд 17Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий
против этого катета, равен 30°.
Рассмотрим прямоугольный треугольник АВС, у которого
катет АС равен половине гипотенузы ВС. Докажем, что ∠АВС=30°Приложим к треугольнику АВС равный
ему треугольник АВД, получим равно-
сторонний треугольник ВСД, где
∠Д=∠С=∠ДВС=60°.
∠ДВС=2∠АВС, следовательно,
∠АВС=30°.
1
В
С
А
Д
1
2
3
4
Слайд 18Признаки равенства прямоугольных треугольников.
Если катеты одного прямоугольного треугольника соответственно равны
катетам другого, то такие треугольники равны.
Слайд 19Признаки равенства прямоугольных треугольников.
Если катет и прилежащий к нему острый
угол одного прямоугольного треугольника соответственно равны катету и прилежащему к
нему острому углу другого, то такие треугольники равны.
Слайд 20Признаки равенства прямоугольных треугольников.
Если гипотенуза и острый угол одного прямоугольника
соответственно равны гипотенузе и острому углу другого, то такие треугольники
равны.
Слайд 21Признаки равенства прямоугольных треугольников
Если гипотенуза и катет одного прямоугольника соответственно
равны гипотенузе и катету другого, то такие треугольники равны.
