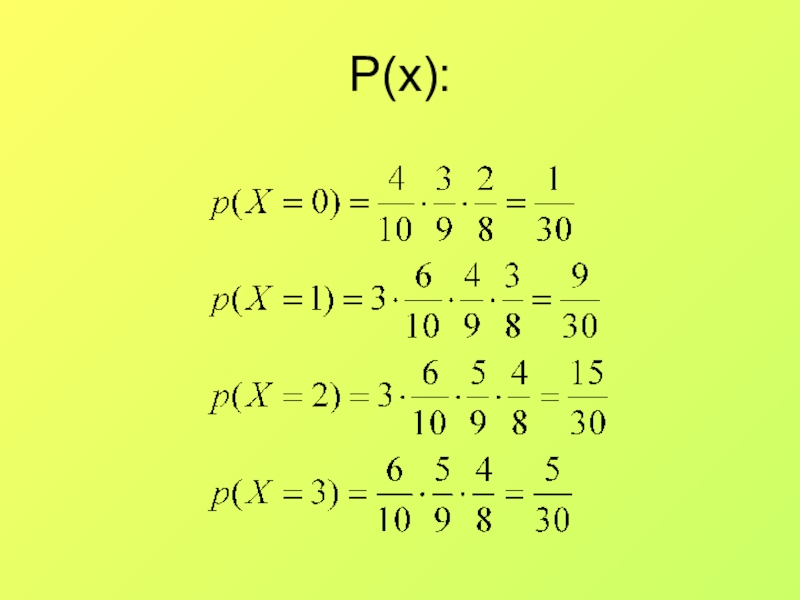Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок № 86 Тема: Случайная величина. Дискретные и непрерывные случайные
Содержание
- 1. Урок № 86 Тема: Случайная величина. Дискретные и непрерывные случайные
- 2. При оценивании случайных событий важно изучение числовых
- 3. Понятие о случайной величине Пусть имеется
- 4. Слайд 4
- 5. Случайную величину можно создать и искусствено
- 6. Классификация
- 7. Слайд 7
- 8. Слайд 8
- 9. Определите, где НСВ и ДСВЧисло очков, выпавших
- 10. Слайд 10
- 11. Распределение дискретной случайной величины Пусть
- 12. Распределения случайных величин могут быть
- 13. Конечное распределение Если мы имеем конечное распределение случайной величины x, принимающей n значений, то:
- 14. Бесконечное распределение
- 15. Слайд 15
- 16. Пример В урне находится 6 белых
- 17. Очевидно, что x может принимать
- 18. P(x):
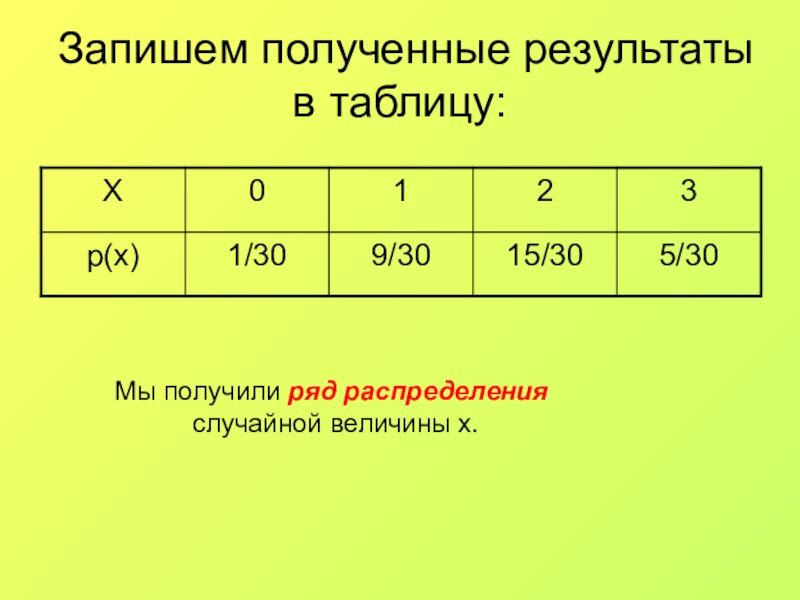
- 19. Запишем полученные результаты в таблицу:Мы получили ряд распределения случайной величины x.
- 20. Распределение случайной величины Пусть случайная величина
- 21. Слайд 21
- 22. Скачать презентанцию
При оценивании случайных событий важно изучение числовых свойств и оценивание этих событий.Для определения числовых характеристик в теории вероятностей вводится понятие случайная величина (СВ)
Слайды и текст этой презентации
Слайд 1 Урок № 86 Тема: Случайная величина. Дискретные и непрерывные случайные величины. Закон распределения
дискретной случайной величины (ДСВ)
Слайд 2При оценивании случайных событий важно изучение числовых свойств и оценивание
этих событий.
Для определения числовых характеристик в теории вероятностей вводится понятие
случайная величина (СВ)Слайд 3Понятие о случайной величине
Пусть имеется величина x, которая
может принимать то или иное значение, причем это значение может
быть различным при неизменных условиях постановки опыта. Такая величина носит название случайной величины.Слайд 5Случайную величину можно создать и искусствено
Приведем примеры перехода
от событий к случайным величинам. Пусть из урны наудачу выбирается шары,
причем известно, что в урне имеются шары красного, синего и зеленого цветов. Вводим случайную величину x, принимающую значения: x = 1, если вынутый шар оказался зеленым x = 2, если вынутый шар оказался красным x = 3, если вынутый шар оказался синим. Таким образом мы совершили переход от событий к случайной величине.Слайд 9Определите, где НСВ и ДСВ
Число очков, выпавших при бросании кубика.
Спортсмен
бросает копье. Случайная величина – дальность броска
Слайд 11 Распределение дискретной случайной величины
Пусть дана случайная величина
x и множество значений этой величины {xk}. Пусть известны вероятности
событий p(xk)-вероятности, что случайная величина x примет значение xk. Тогда говорят, что задано дискретное распределение случайной величиныСлайд 12 Распределения случайных величин могут быть конечными и бесконечными.
Примером конечного распределения может служить распределение случайной величины x -
числа попаданий в цель при трех выстрелах. Очевидно,что x принимает значения из множества {0, 1, 2, 3}. Данное распределение конечное. Примером бесконечного распределения может служить распределение случайной величины x - числа выбрасывания двух кубиков до тех пор, пока не выпадет 12 очков. Очевидно, что теоретически величина x может принимать сколь угодно большие значения. Данное распределение бесконечное.Важнейшие особенности случайных величин