Условная развертка на основе аппроксимации цилиндрическими или коническими

g
 – поверхность вращения

i  П1
Поверхность α ,

Поверхности вращения

оси вращения i, называется параллелью


горло
горло
экватор
экватор
Параллель с минимальным радиусом называется горлом
Параллель

Любая точка на поверхности вращения вращаясь вокруг оси описывает окружность-параллель.

i, называется меридианом
m
Главный меридиан
меридиан
λ1гм
λ1
Пересечение поверхности фронтальной плоскостью уровня, проходящей через

Главный меридиан является границей видимости

открытый тор (кольцо), закрытый тор, а так же эллипсоид вращения,

поверхности
Принадлежность точки поверхности

=S)
ℓ2
S1
i1
ℓ1
(А2)
А1
i2
S2
m2
S1
i1
m1
Точка на поверхности конуса
R
Точки на поверхности вращения находятся с помощью

дуги радиусом R, называется глобоидом

сечением
Линия пересечения поверхности с плоскостью является линией, одновременно принадлежащей поверхности

Пересечение поверхности вращения
с проецирующей плоскостью

плоскостью

t2

t1

t3

t

βП2;

β2 ≡t2

Ф2

t1

В1

В2

А2

А1

С1I≡ℓ1I

С2≡С2I

ℓ2≡ℓ2I

С1≡ℓ1

проецирующей плоскостью

http://ru.wikipedia.org/wiki/Файл:Apollonios_of_Perga.jpeg
Аполлоний прославился в первую очередь выдающейся работой «Конические

43
41
4

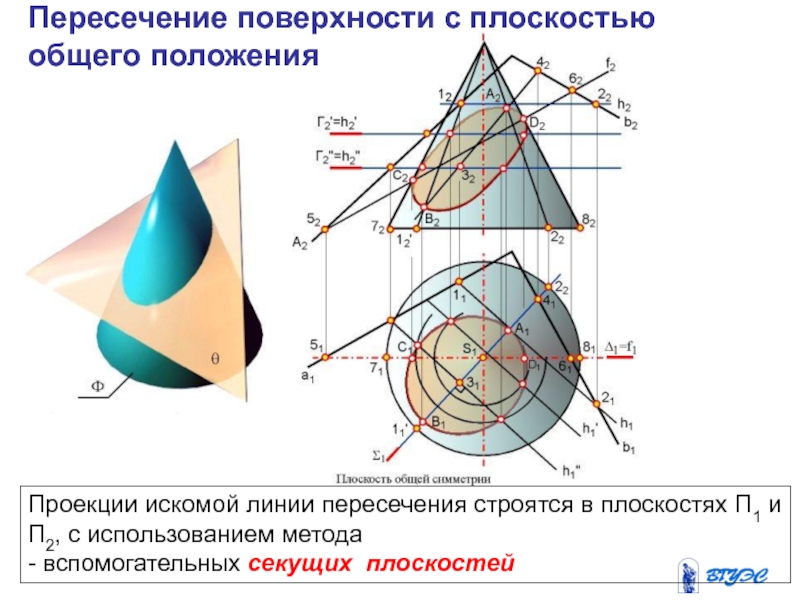
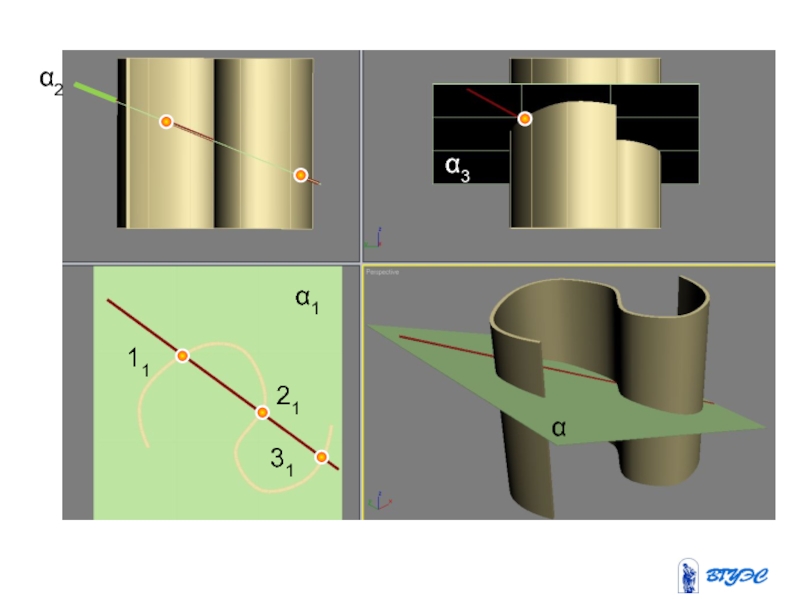
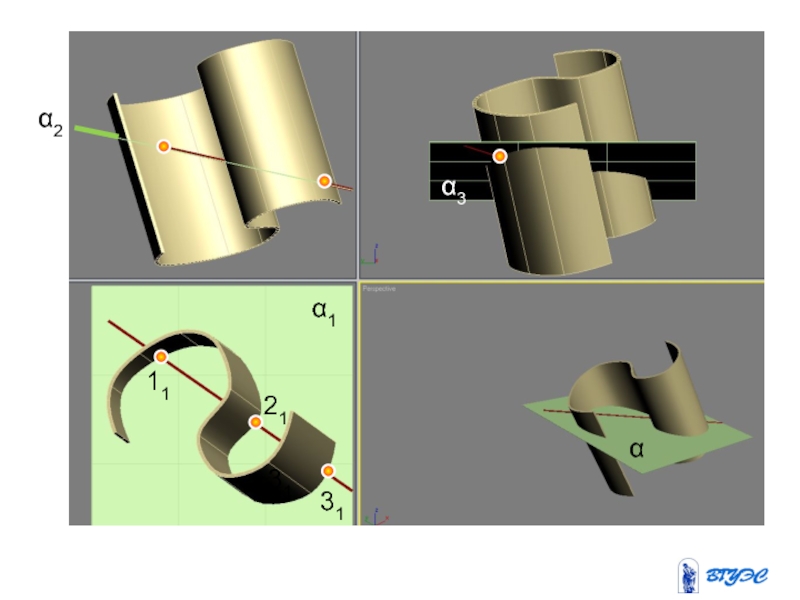
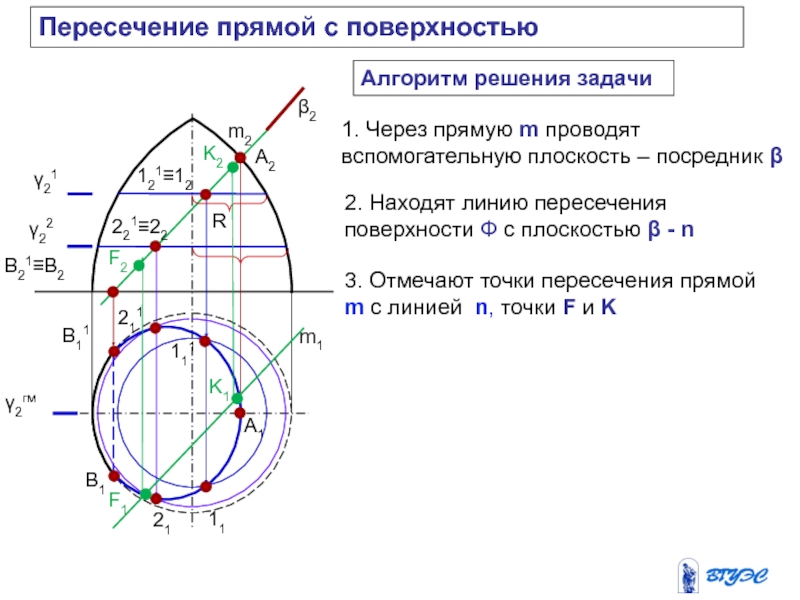
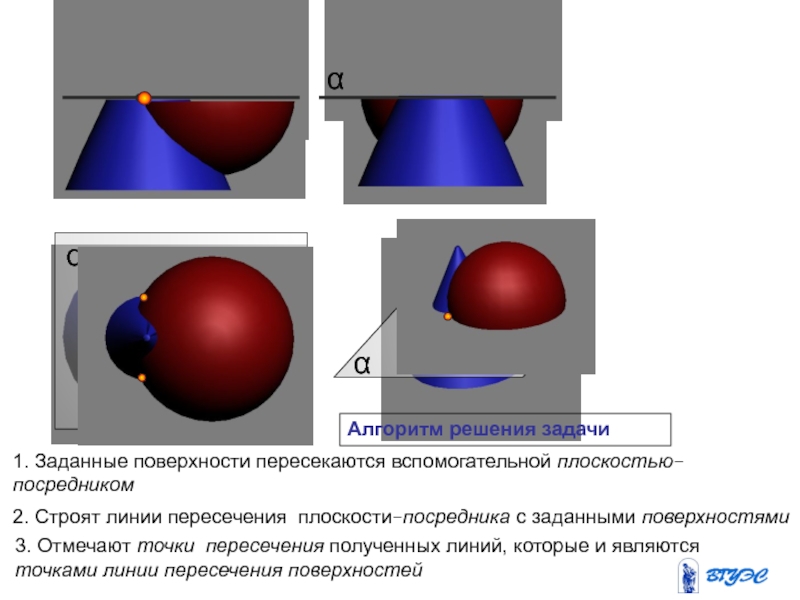
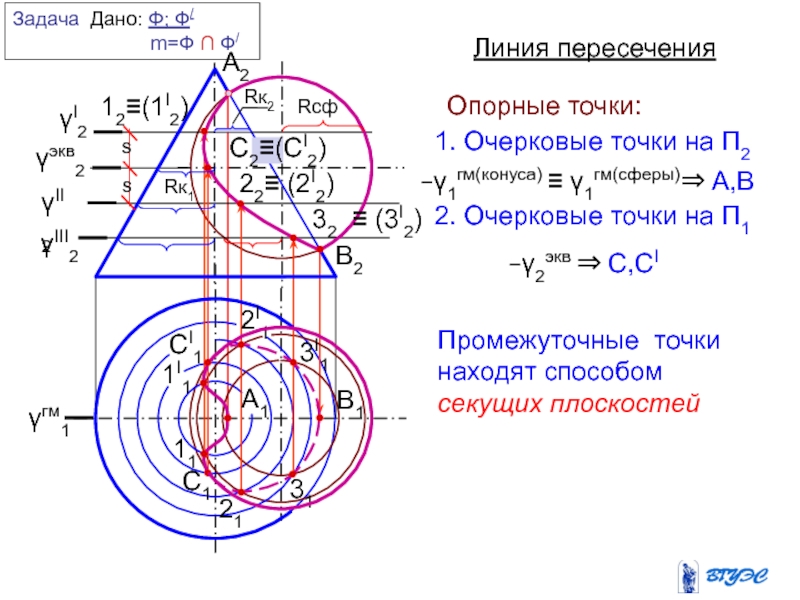
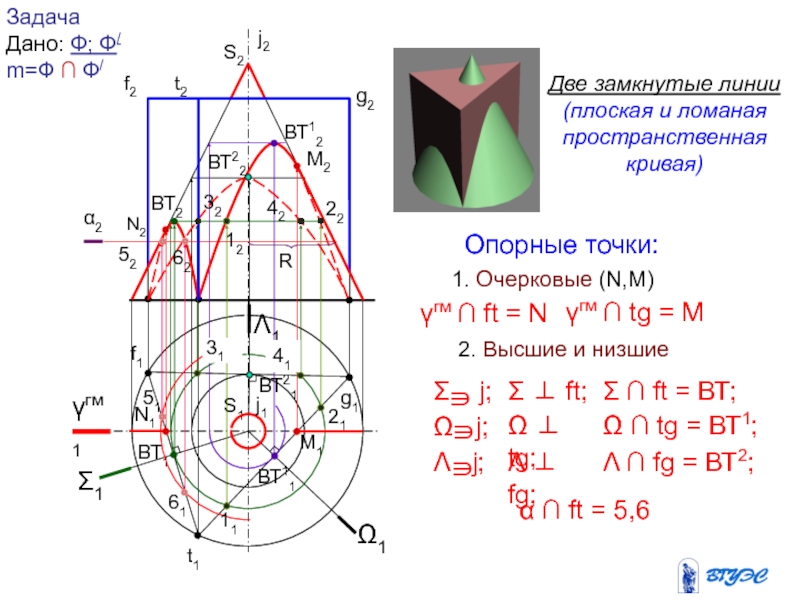
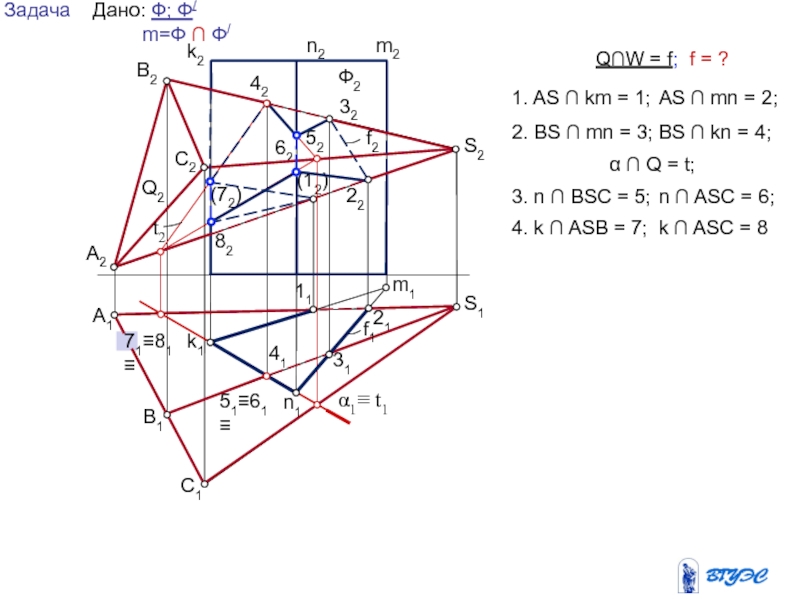
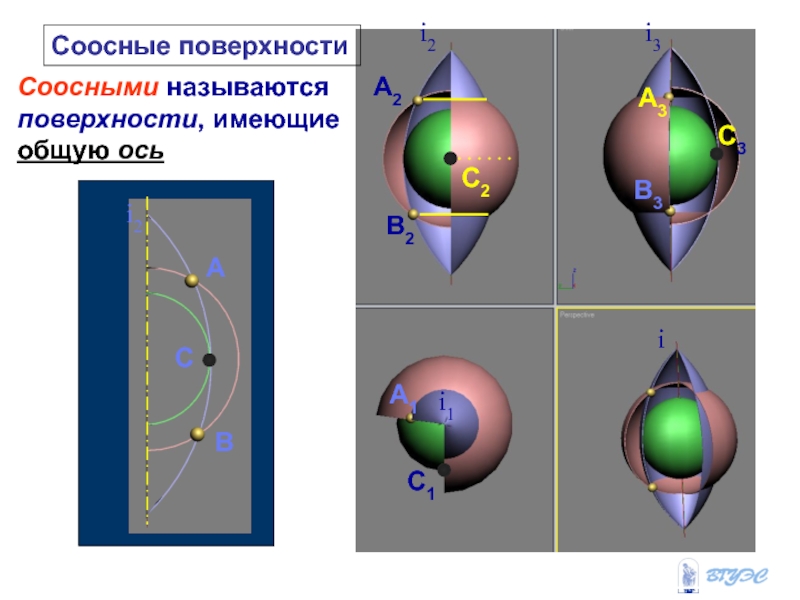
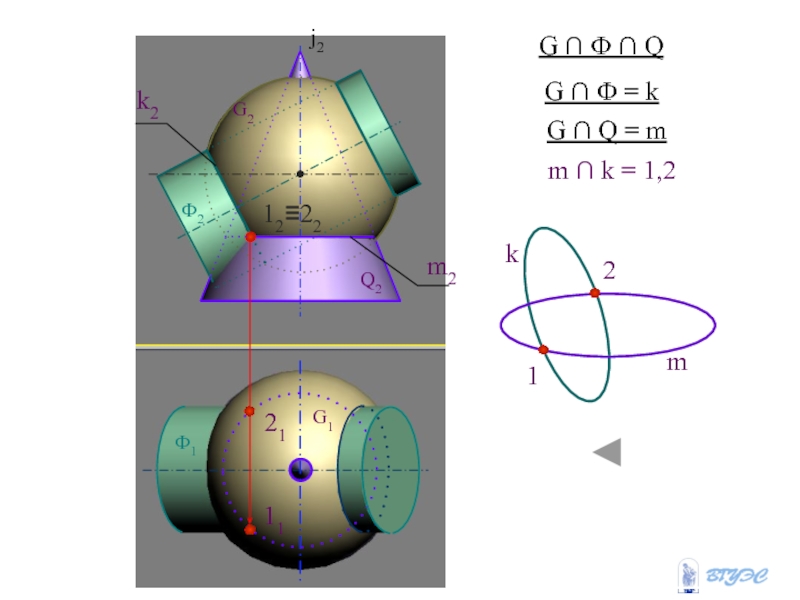
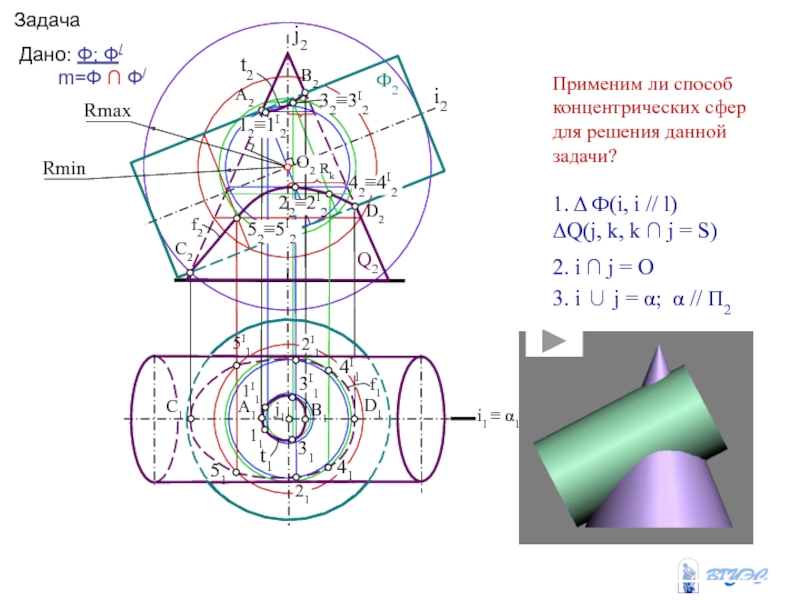
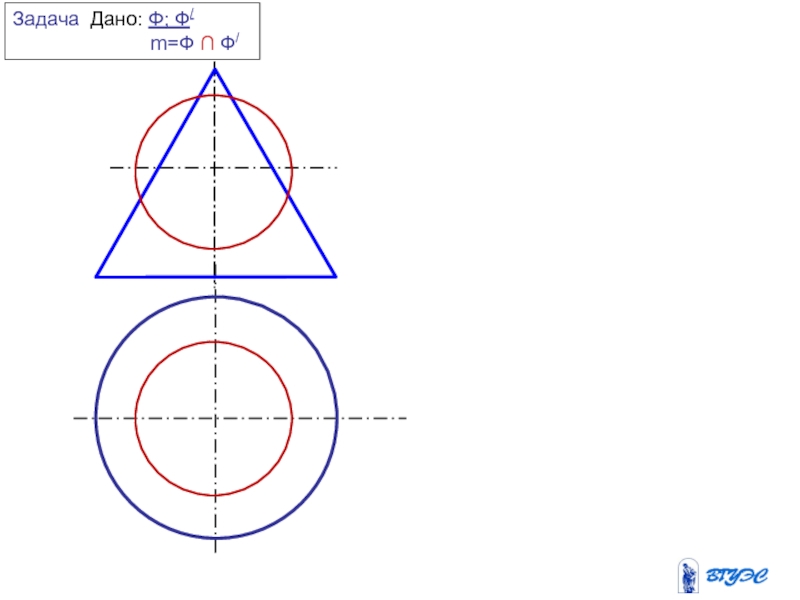
и плоскость пересекают вспомогательной плоскостью посредником  (гамма).
2. Находят линию

3. Находят линию пересечения плоскости-посредника с заданной плоскостью : MN =   .

4.Отмечают точки, в которых эти линии пересекутся: 1,2 – MN  n Точки 1 и 2, являясь общими для данных поверхности и плоскости будут точками искомой линии пересечения.

5. Для построения линии пересечения необходимо найти еще ряд точек (3,4,5…), используя плоскости-посредники

Алгоритм решения задач на пересечение поверхности с плоскостью

которых лежат на проекциях контурных линий одной из поверхностей;

-

2

21

22

А2

А1

111

11

21

211

В1

В11

В21≡В2

221≡22

121≡12

2гм

R

В зависимости от расположения тел по отношению к плоскостям проекций точки пересечения можно получить на одной из проекций.

П2, с использованием метода секущих плоскостей или способом замены плоскостей

с использованием метода
- вспомогательных секущих плоскостей
Пересечение поверхности с плоскостью

плоскость – посредник 
2. Находят линию пересечения поверхности с плоскостью

3. Отмечают точки пересечения прямой АВ с линией k, точки 1 и 2

Количество точек пересечения прямой
с поверхностью определяет порядок последней

проводят вспомогательную плоскость – посредник 
2. Находят линию пересечения поверхности

3. Отмечают точки пересечения прямой m с линией n, точки F и K

с заданными поверхностями
3. Отмечают точки пересечения полученных линий, которые и

Алгоритм решения задачи

m=Ф  Ф/
экв2
I2
II2
гм1
А2
В2
12≡(1I2)
22≡

32 ≡ (3I2)

1I1

11

А1

CI1

2I1

3I1

B1

C1

21

31

Линия пересечения

III2

–1гм(конуса) ≡ 1гм(сферы) А,В

Опорные точки:

1. Очерковые точки на П2

s

s

Промежуточные точки находят способом секущих плоскостей

Rк2

Rсф

2. Очерковые точки на П1

–2экв  С,СI

Rк1

C2≡(CI2)

Две замкнутые линии (плоская и ломаная пространственная кривая)
Опорные точки:
2. Высшие

1. Очерковые (N,M)

гм1

N1

M1

M2

N2

гм  ft = N

гм  tg = M

1

j1

j2

 j;



  ft;

  ft = ВТ;

 j;



  tg;

  tg = ВТ1;

 j;



  fg;

  fg = ВТ2;

1

1

ВТ2

ВТ11

ВТ12

ВТ21

ВТ22

11

21

12

22

31

41

32

42

51

61

52

62

2

R

  ft = 5,6

первого многогранника с гранями второго и ребер второго с гранями

Способ граней  построение сторон ломаной как отрезков прямых попарного пересечения граней данных многогранников

прямыми соединяются проекции только тех точек, которые принадлежат одной грани

2;
2. BS ∩ mn = 3;
BS ∩ kn =

3. n ∩ BSC = 5;

n ∩ ASC = 6;

4. k ∩ ASB = 7;

k ∩ ASC = 8

5161

7181

(72)

82

52

62

α1 t1

t2

 ∩ Q = t;

Q∩W = f; f = ?

f1

f2

Задача Дано: Ф; Ф/
m=Ф  Ф/

Ф2

Q2

вращения поверхностей пересекаются
3. Пересекающиеся оси вращения образуют плоскость уровня, или

k = 1,2
k
m
1
2
21
11
12≡22
k2
m2
Ф1
G1
G  Ф  Q

k ∩ j = S)

2. i ∩ j = О

3.

О2

Rk

B2

222I2

424I2

525I2

Применим ли способ концентрических сфер для решения данной задачи?

C1

21

2I1

3I1

41

4I1

5I1

Задача
Дано: Ф; Ф/
m=Ф  Ф/

m=Ф  Ф/