TheSlide.ru

Введение. Моделирование атомно-молекулярных структур

Содержание

1. Введение. Моделирование атомно-молекулярных структур
2. АктуальностьСтруктура и химический состав определяют свойства объектов
3. Молекулярная динамикаУравнения:Ковалентные взаимодействияНе ковалентные взаимодействия
4. Силовое поле, эмпирические константыКонстанты из уравнения :1)
5. АлгоритмСумма сил действующих на атомРасчет новых координатDtинтегрирование
6. Возможности МДравновесные свойства:Константы связиСредняя потенциальная энергия системыРавновесная
7. Ограничения МДИспользуются законы НьютонаНе учитываются электроныСиловые поля – это приближениеУдаленные взаимодействия не учитываютсяГраничные условия не натуралистичны
8. Квантовая химияСтационарное уравнение Шрёдингера:Атомная система единиц:Для многочастичной
9. Верификация моделейИК спектроскопияЭксперимент (1)DFT, 6-21GПараметры термохимии (тепловой эффект)Сравнение с более строгими моделями
10. ВыводыТеоретический инструментарий исследований в размерном диапазоне 10-8
11. Стационарная теория возмущений. Невырожденный случай.
12. Постановка задачиРассматривается возмущенное уравнение Шрёдингера:Пусть для невозмущенного оператора известно точное решениеТребуется получить решение для возмущенного оператора(1)(2)
13. Решение. Учет малости возмущенияИспользуя разложение в ряд
14. Решение. Первая поправка к энергиямСистема собственных функций
15. Решение. Первая поправка к ψНеобходимо найти коэффициенты разложения(6)
16. Решение. Первая поправка к ψКоэффициент ann(7)
17. РезультатПервая поправка к энергииПервая поправка к волновой функцииРяд сходится при
18. Д.З.: Флюгге. Задачи по квантовой механике. Т.2, №181. Рассмотреть стационарный случай
19. Скачать презентанцию

АктуальностьСтруктура и химический состав определяют свойства объектов

Главная
Разное
Введение. Моделирование атомно-молекулярных структур

Слайды и текст этой презентации

Слайд 1Введение. Моделирование атомно-молекулярных структур

Введение. Моделирование атомно-молекулярных структур

Слайд 2Актуальность
Структура и химический состав
определяют свойства объектов

АктуальностьСтруктура и химический состав определяют свойства объектов

Слайд 3Молекулярная динамика
Уравнения:

Ковалентные взаимодействия
Не ковалентные взаимодействия

Молекулярная динамикаУравнения:Ковалентные взаимодействияНе ковалентные взаимодействия

Слайд 4Силовое поле, эмпирические константы
Константы из уравнения :
1) связи , Кb,

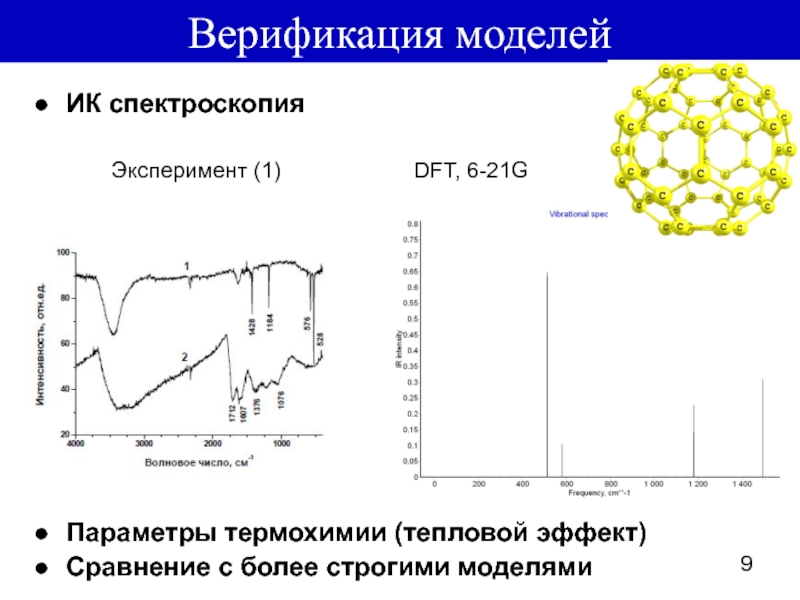
b0 ИК-спектроскопия, QM
2) углы K,0 ИК-спектроскопия, QM
3) торсионные углы K,  ИК-спектроскопия,

ЯМР, QM
4) Частичные заряды qi угадывание, термодинамика,QM
5) Параметры WdV Aij, Cij угадывание, термодинамика, QM

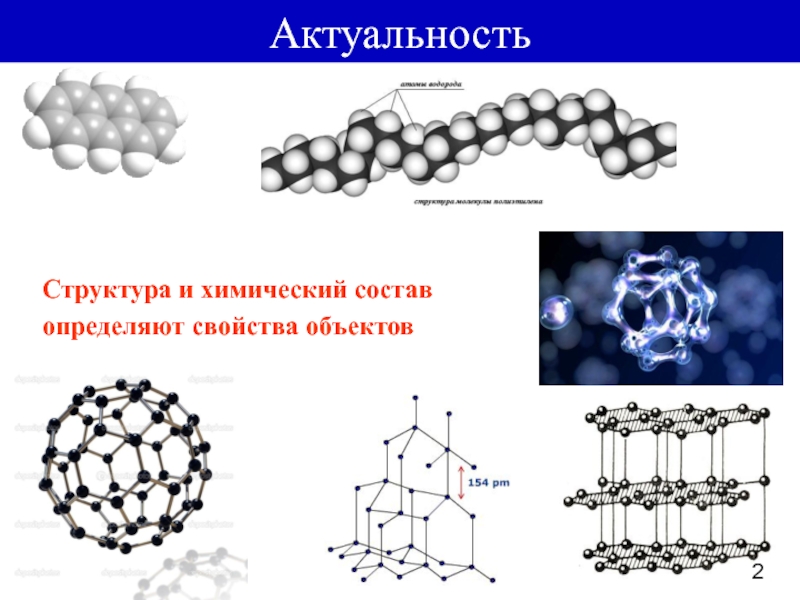
Большинство значений можно получить из высокоточных расчётов QM ab initio. Полученные значения "подгоняют" под уравнения силового поля.

Силовое поле, эмпирические константыКонстанты из уравнения :1) связи , Кb, b0 ИК-спектроскопия, QM2) углы K,0 ИК-спектроскопия, QM3) торсионные

Слайд 5Алгоритм
Сумма сил действующих
на атом
Расчет новых координат
Dt
интегрирование

АлгоритмСумма сил действующих на атомРасчет новых координатDtинтегрирование

Слайд 6Возможности МД
равновесные свойства:
Константы связи
Средняя потенциальная энергия системы
Равновесная геометрия

динамические и неравновесные

свойства:
Вязкость жидкости
Процесс диффузии в мембраны
Динамика фазовых изменений
Кинетику реакции

Размеры систем

– до 106 атомов!!!

Возможности МДравновесные свойства:Константы связиСредняя потенциальная энергия системыРавновесная геометриядинамические и неравновесные свойства:Вязкость жидкостиПроцесс диффузии в мембраны Динамика фазовых

Слайд 7Ограничения МД
Используются законы Ньютона
Не учитываются электроны
Силовые поля – это приближение
Удаленные

взаимодействия не учитываются
Граничные условия не натуралистичны

Ограничения МДИспользуются законы НьютонаНе учитываются электроныСиловые поля – это приближениеУдаленные взаимодействия не учитываютсяГраничные условия не натуралистичны

Слайд 8Квантовая химия
Стационарное уравнение Шрёдингера:
Атомная система единиц:
Для многочастичной системы:
H, T, U

– операторы Гамильтона, кинетической и потенциальной энергии; Z – заряд

ядра; r – расстояние между частицами; Δ – оператор Лапласа; индексы a и b – номера ядер; i и j – номера электронов

Квантовая химияСтационарное уравнение Шрёдингера:Атомная система единиц:Для многочастичной системы: H, T, U – операторы Гамильтона, кинетической и потенциальной энергии;

Слайд 9Верификация моделей
ИК спектроскопия
Эксперимент (1)
DFT, 6-21G
Параметры термохимии (тепловой эффект)
Сравнение с более

строгими моделями

Верификация моделейИК спектроскопияЭксперимент (1)DFT, 6-21GПараметры термохимии (тепловой эффект)Сравнение с более строгими моделями

Слайд 10Выводы
Теоретический инструментарий исследований в размерном диапазоне 10-8 – 10-10 существует

Ограничения:
Вычислительные ресурсы
Возможности программных пакетов
Начальные и граничные условия

Основные проблемы:
Постановка задачи
Обоснование выбранной

модели
Анализ результатов

ВыводыТеоретический инструментарий исследований в размерном диапазоне 10-8 – 10-10 существует Ограничения:Вычислительные ресурсыВозможности программных пакетовНачальные и граничные условияОсновные

Слайд 11Стационарная теория возмущений. Невырожденный случай.

Стационарная теория возмущений. Невырожденный случай.

Слайд 12Постановка задачи
Рассматривается возмущенное уравнение Шрёдингера:
Пусть для невозмущенного оператора известно точное

решение
Требуется получить решение для возмущенного оператора
(1)
(2)

Постановка задачиРассматривается возмущенное уравнение Шрёдингера:Пусть для невозмущенного оператора известно точное решениеТребуется получить решение для возмущенного оператора(1)(2)

Слайд 13Решение. Учет малости возмущения
Используя разложение в ряд Тейлора по степеням

малого возмущения получим:
Учтем, что
Подставим (3)(1) и приравняем члены одинакового

порядка малости. Получим

(3)

(4)

Решение. Учет малости возмущенияИспользуя разложение в ряд Тейлора по степеням малого возмущения получим:Учтем, что Подставим (3)(1) и

Слайд 14Решение. Первая поправка к энергиям
Система собственных функций ортонормальна и полна
Теорема

о собственных функциях эрмитова оператора (Владимиров В.С. Уравнения математической физики.

– М., 1971. – С.42-43)
Теорема Стеклова (Там же, С. 345 – 346)

Для первой поправки к энергии получим:

(5’)

(5)

Решение. Первая поправка к энергиямСистема собственных функций ортонормальна и полнаТеорема о собственных функциях эрмитова оператора (Владимиров В.С.

Слайд 15Решение. Первая поправка к ψ
Необходимо найти коэффициенты разложения
(6)

Решение. Первая поправка к ψНеобходимо найти коэффициенты разложения(6)

Слайд 16Решение. Первая поправка к ψ
Коэффициент ann
(7)

Решение. Первая поправка к ψКоэффициент ann(7)

Слайд 17Результат
Первая поправка к энергии
Первая поправка к волновой функции
Ряд сходится при

РезультатПервая поправка к энергииПервая поправка к волновой функцииРяд сходится при

Слайд 18Д.З.: Флюгге. Задачи по квантовой механике. Т.2, №181. Рассмотреть стационарный случай

Д.З.: Флюгге. Задачи по квантовой механике. Т.2, №181. Рассмотреть стационарный случай

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей