Взаимное положение прямой и плоскости, двух плоскостей

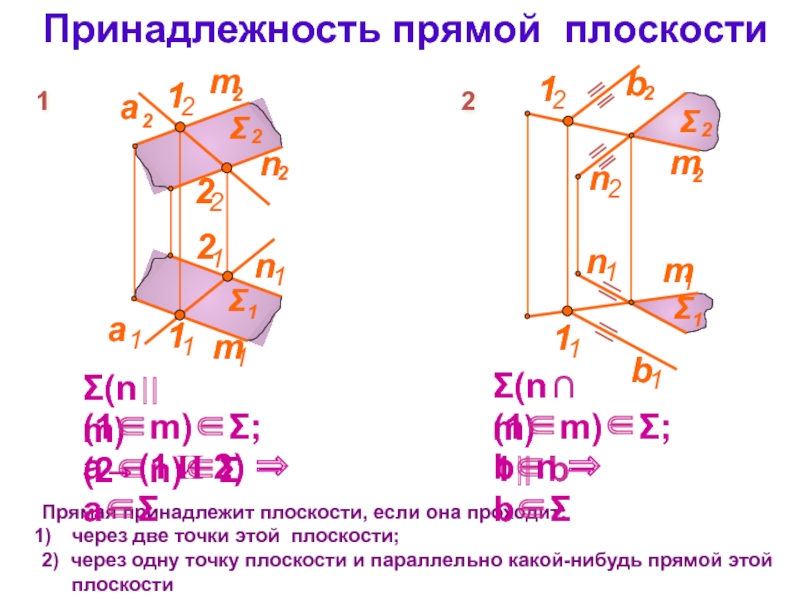
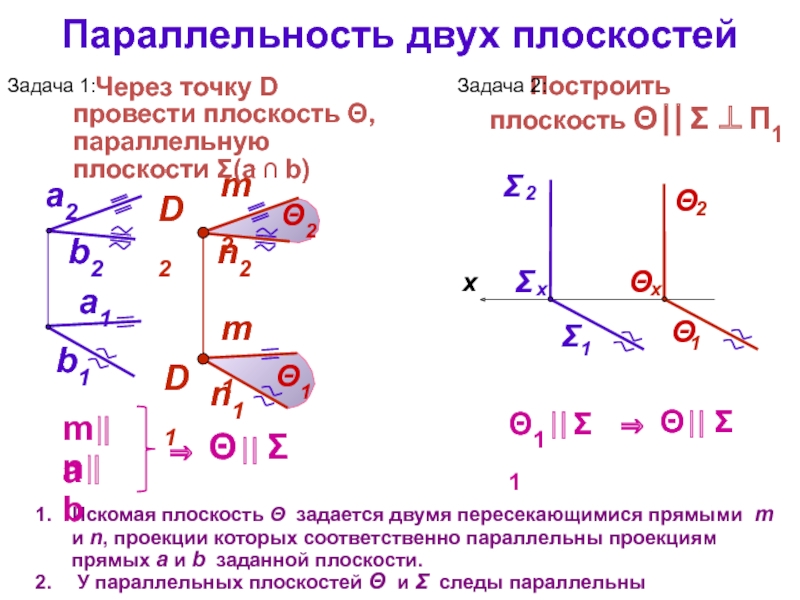
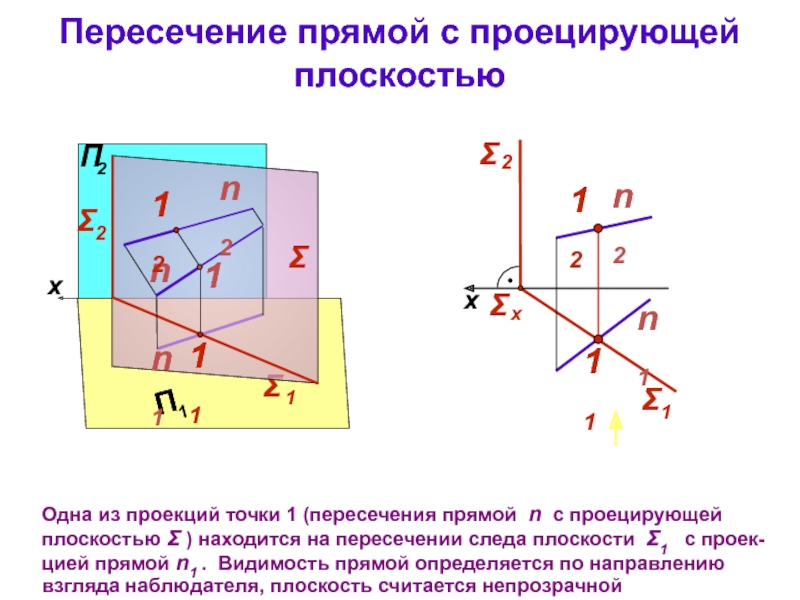
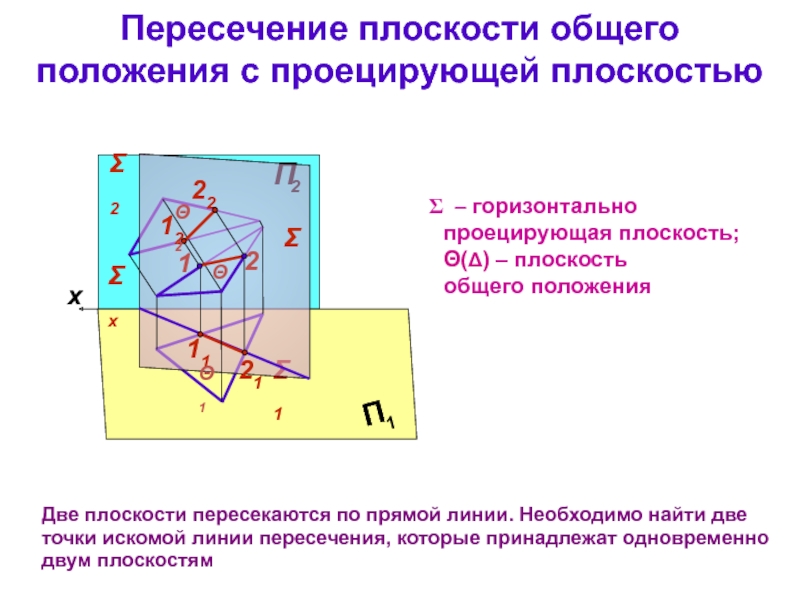
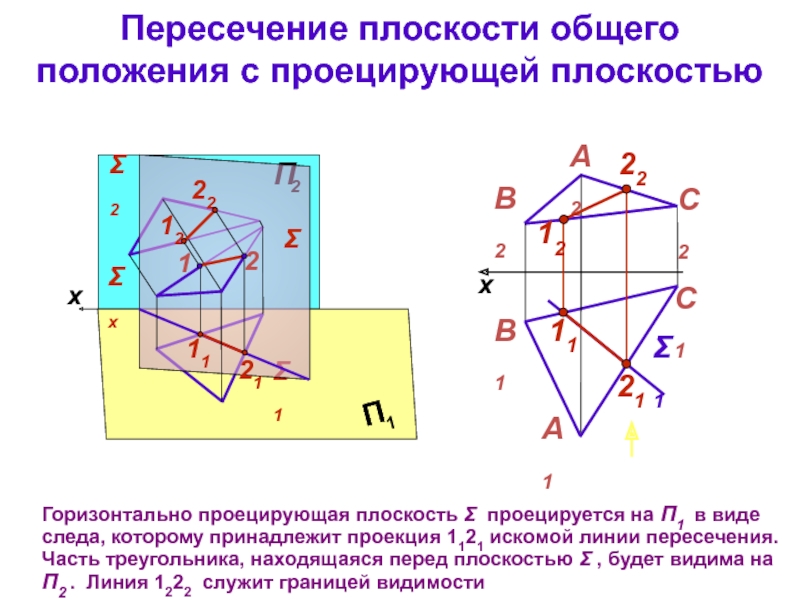
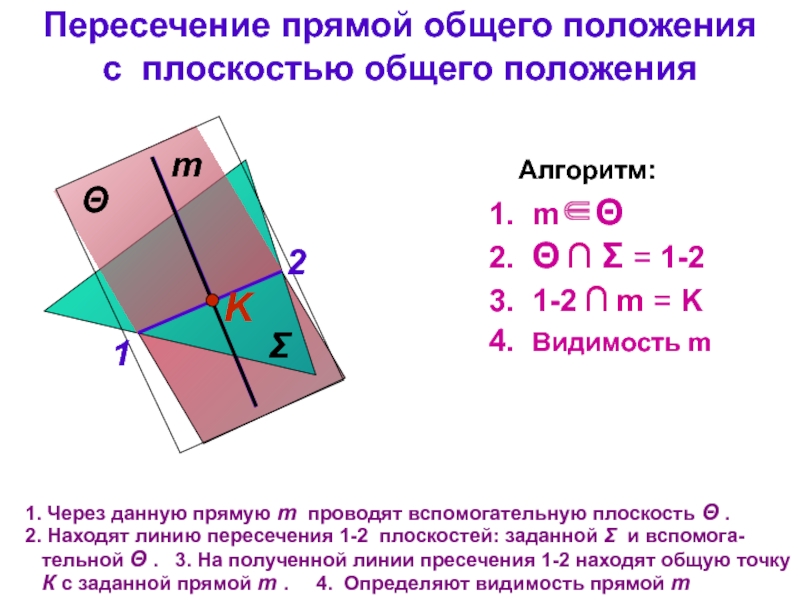
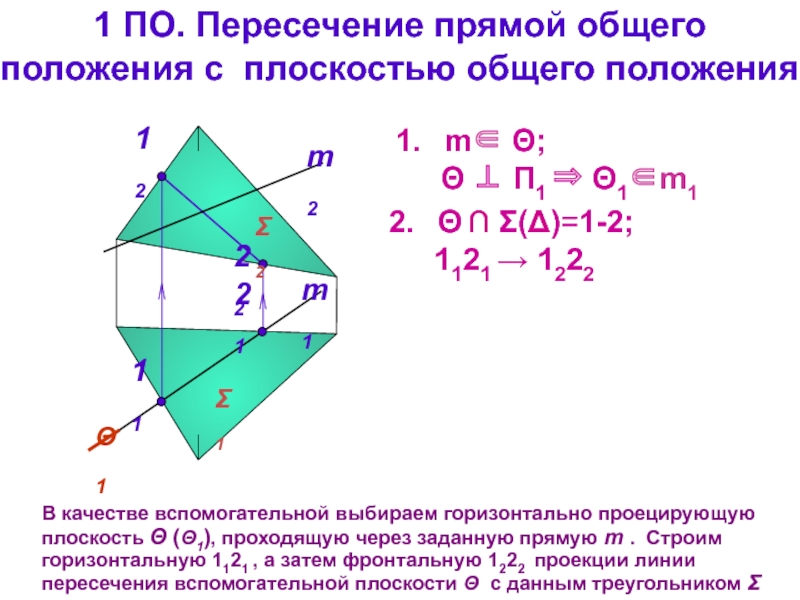
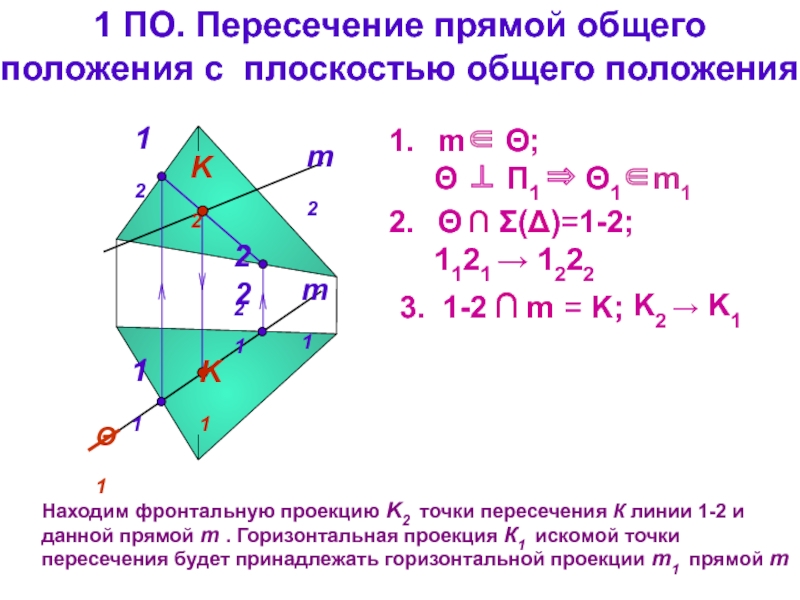
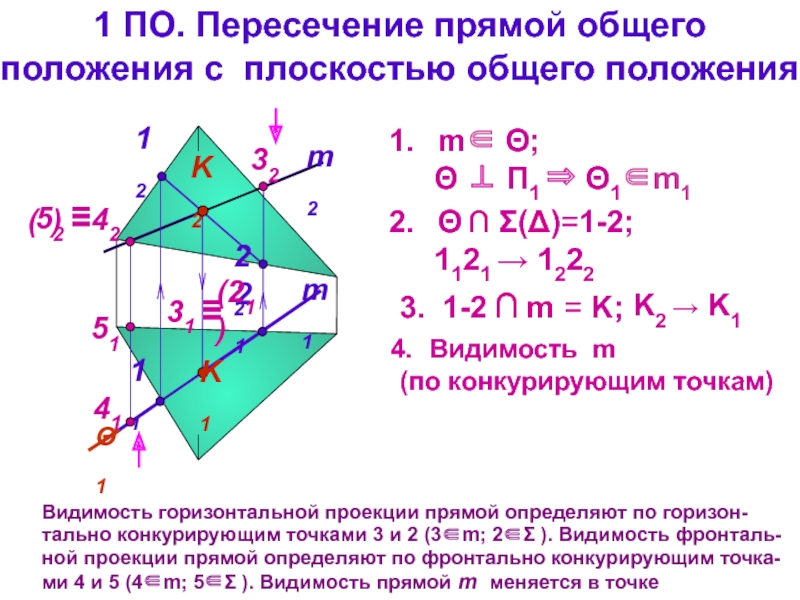
тема 3): все точки прямой являются точками плоскости
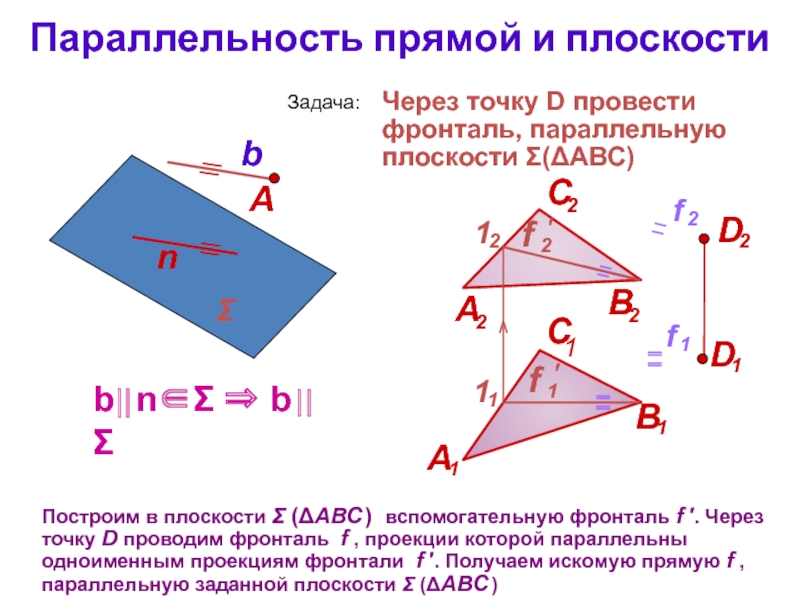
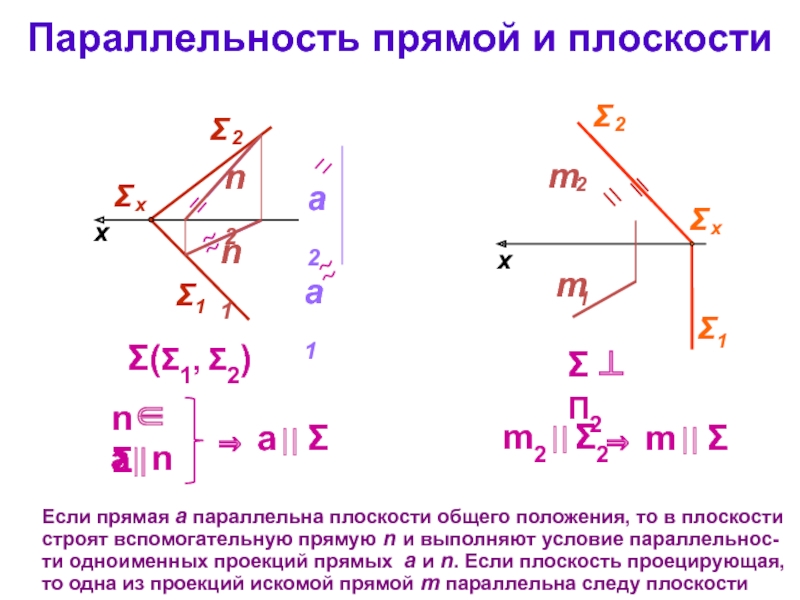
Прямая параллельна плоскости:

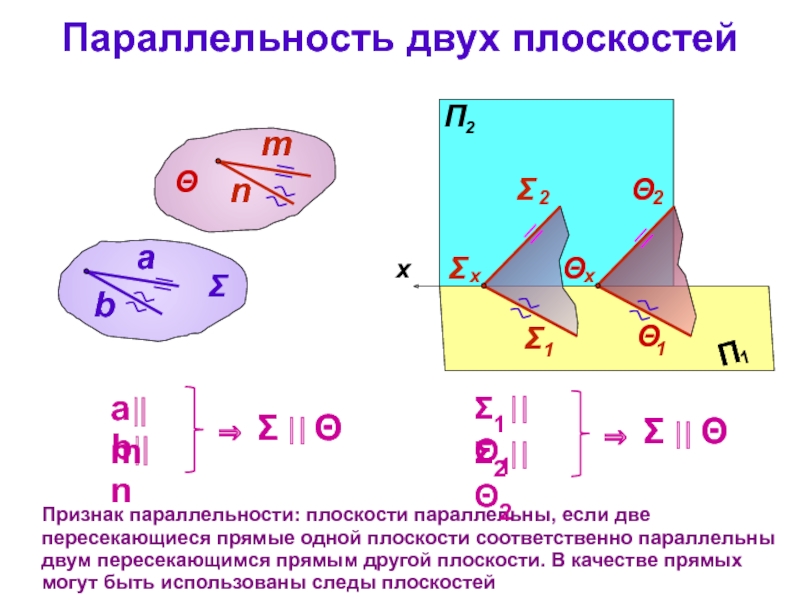
Плоскости параллельны: общих прямых нет
Плоскости пересекаются: одна общая прямая

Прямая и плоскость:

Две плоскости:

точки этой плоскости;
2) через одну точку плоскости и параллельно

Σ(n⎟⎟ m)

1

(1∈m)∈Σ; (2∈n)∈Σ

а→(1 И 2) ⇒ а∈Σ

2

Σ(n ∩ m)

(1∈m)∈Σ; 1∈b

b⎟⎟ n ⇒ b∈Σ

бесчисленное множество прямых линий, параллельных данной плоскости Σ . Для

Σ

b

Прямая параллельна
плоскости, если она
параллельна какой-либо
прямой, лежащей в
этой плоскости

А

Признак параллельности:

b⎟⎟ n∈Σ ⇒ b⎟⎟ Σ

фронталь f ′. Через точку D проводим фронталь f ,

Σ

b

Через точку D провести фронталь, параллельную плоскости Σ(ΔАВС)

Задача:

b⎟⎟ n∈Σ ⇒ b⎟⎟ Σ

А

положения, то в плоскости строят вспомогательную прямую n и выполняют

n1

n2

а2

а⎟⎟ n

x

Σ ⊥ П2

n∈Σ

одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. В

b⎟⎟ n

а⎟⎟ m

Σ1⎟⎟ Θ1

Σ2⎟⎟ Θ2

и n, проекции которых соответственно параллельны проекциям прямых а и

n⎟⎟ b

b1

a1

m⎟⎟ a

Θ1⎟⎟ Σ 1

⇒ Θ⎟⎟ Σ

b2

a2

Через точку D провести плоскость Θ, параллельную плоскости Σ(a ∩ b)

Задача 1:

прямой n с проецирующей плоскостью Σ ) находится на пересечении

n2

прямой линии. Необходимо найти две точки искомой линии пересечения, которые

– горизонтально
проецирующая плоскость;
Θ(Δ) – плоскость
общего положения

Θ

Θ1

Θ2

проецируется на П1 в виде следа, которому принадлежит проекция 1121

прямую m проводят вспомогательную плоскость Θ .
Находят линию

Алгоритм:

1. m∈Θ

2. Θ ∩ Σ = 1-2

3. 1-2 ∩ m = K

4. Видимость m

качестве вспомогательной выбираем горизонтально проецирующую плоскость Θ (Θ1), проходящую через

m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1

Θ ∩ Σ(Δ)=1-2;
1121 → 1222

Σ1

Σ2

фронтальную проекцию K2 точки пересечения К линии 1-2 и данной

m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1

Θ ∩ Σ(Δ)=1-2;
1121 → 1222

горизонтальной проекции прямой определяют по горизон-тально конкурирующим точками 3 и

21

Видимость m
(по конкурирующим точкам)

(21)

( )

m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1

Θ ∩ Σ(Δ)=1-2;
1121 → 1222