Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Занятие 21. (2 часа) Растяжение и сжатие. Продольные и поперечные деформации
Содержание
- 1. Занятие 21. (2 часа) Растяжение и сжатие. Продольные и поперечные деформации
- 2. 21.1. Деформации при растяжении и сжатииРассмотрим деформацию
- 3. В сопротивлении материалов принято рассчитывать деформации в
- 4. 21.2. Закон ГукаВ пределах упругих деформаций деформации
- 5. 21.3. Формулы для расчета перемещений поперечных сечений
- 6. 21.4. Выводы1. Абсолютное удлинение бруса прямо пропорционально
- 7. 3. Поперечные деформации меньше продольных и редко
- 8. При работе пластические деформации не должны возникать,
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Занятие 22. (2 часа) Механические испытания, механические характеристики. Предельные и допускаемые напряжения.
- 13. 22.1. Механические испытания. Статические испытания на растяжение
- 14. На рис. 22.2 изображена схема образца до
- 15. Машина снабжена прибором для автоматической записи диаграммы
- 16. Полученная диаграмма пересчитывается и перестраивается (рис. 22.4
- 17. 1) точка 1 соответствует пределу пропорциональности: после
- 18. 3) точка 3 является концом участка, на
- 19. 22.2. Механические характеристикиПри построении приведенной диаграммы рассчитываются
- 20. б) Характеристики пластичности материалаδ — максимальное удлинение
- 21. 22.3. Виды диаграмм растяженияРазличные материалы по-разному ведут
- 22. Ко второй группе относятся хрупкие материалы, эти
- 23. Таким образом, хрупкий и пластично-хрупкий материалы не
- 24. 22.4. Предельные и допустимые напряженияПредельным напряжением считают
- 25. Для пластично-хрупких материалов предельным напряжением считают напряжение,
- 26. Примечание. В квадратных скобках принято обозначать допускаемое
- 27. 22.5. Расчеты на прочность при растяжении и
- 28. Существуют три вида расчета на прочность.1. Проектировочный
- 29. Слайд 29
- 30. Слайд 30
- 31. Занятие 23. (2 часа) Кручение. Внутренние силовые
- 32. 23.1. Деформации при крученииКручение круглого бруса происходит
- 33. Связь между угловыми деформациями определяется соотношениемl —
- 34. 23.2. Гипотезы при кручении1. Выполняется гипотеза плоских
- 35. 23.3. Внутренние силовые факторы при крученииКручением называется
- 36. Внешний момент пары сил разворачивает участок бруса
- 37. С помощью интегрирования получим суммарный момент сил
- 38. 23.4. Эпюры крутящих моментовКрутящие моменты могут меняться
- 39. Примеры решения задачПример 1. На распределительном валу
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. 23.5. Напряжения при крученииПроводим на поверхности бруса
- 44. Рассмотрим элемент бруса 1234 после деформации.Рис.23.5.При
- 45. Материал подчиняется закону Гука. Касательное напряжение пропорционально
- 46. 23.6. Максимальные напряжения при крученииДля круглого сечения
- 47. Условие прочности при кручении1. Разрушение бруса при
- 48. 23.7. Виды расчетов на прочностьСуществует три вида
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 221.1. Деформации при растяжении и сжатии
Рассмотрим деформацию бруса под действием
продольной силы F (рис. 21.1).
Начальные размеры бруса:
lo— начальная длина,
αо — начальная ширина.
Брус удлиняется на величину Δl;
Δl— абсолютное удлинение.
При растяжении поперечные размеры уменьшаются,
Δα — абсолютное сужение;
Δl > 0; Δα < 0.
При сжатии выполняется соотношение Δl < 0; Δα > 0.
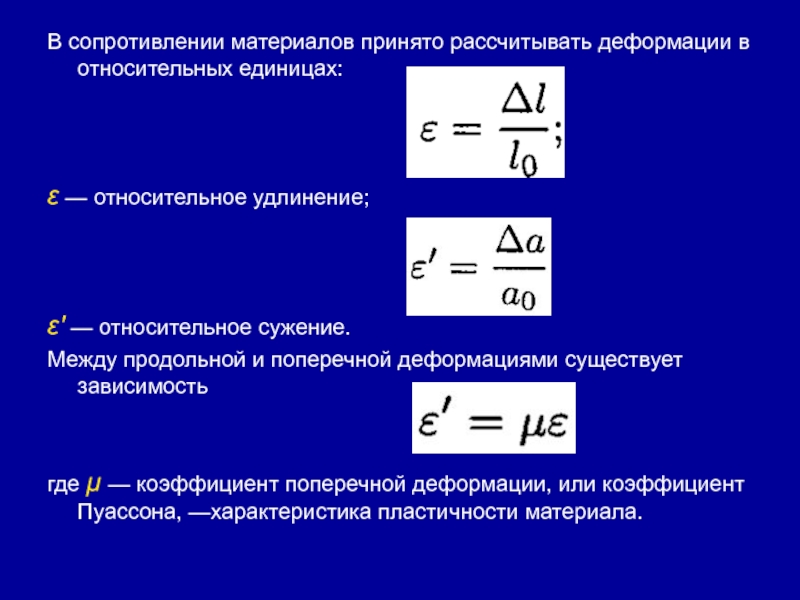
Слайд 3В сопротивлении материалов принято рассчитывать деформации в относительных единицах:
ε —
относительное удлинение;
ε' — относительное сужение.
Между продольной и поперечной деформациями
существует зависимостьгде μ — коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.
Слайд 421.2. Закон Гука
В пределах упругих деформаций деформации прямо пропорциональны нагрузке:
где
F — действующая нагрузка; k — коэффициент.
В современной форме:
Получим зависимость
где Е — модуль упругости, характеризует жесткость материала.
В пределах упругости нормальные напряжения пропорциональны относительному удлинению.
Значение Е для сталей в пределах (2…2,1) • 10-5 МПа.
При прочих равных условиях, чем жестче материал, тем меньше он деформируется:
Слайд 521.3. Формулы для расчета перемещений поперечных сечений бруса при растяжении
и сжатии
Закон Гука
Откуда
Относительное удлинение
В
результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:где Δl — абсолютное удлинение, мм;
σ — нормальное напряжение, МПа;
l — начальная длина, мм;
Е — модуль упругости материала, МПа;
N — продольная сила, Н;
А — площадь поперечного сечения, мм2;
Произведение АЕ называют жесткостью сечения.
Слайд 621.4. Выводы
1. Абсолютное удлинение бруса прямо пропорционально величине продольной силы
в сечении, длине бруса и обратно пропорционально площади поперечного сечения
и модулю упругости.2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом, Пуассона, называемом коэффициентом поперечной деформации.
Коэффициент Пуассона:
у стали μ от 0,25 до 0,3;
у пробки μ = 0:
у резины μ = 0,5.
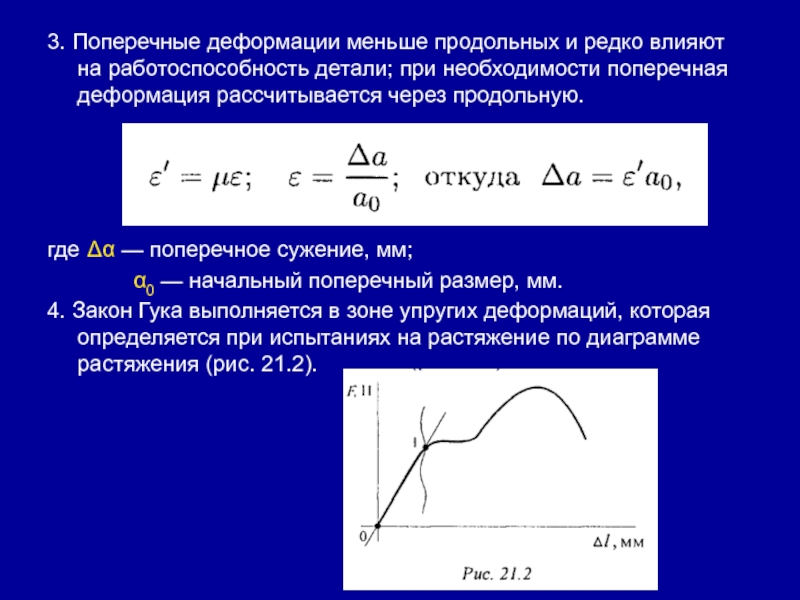
Слайд 73. Поперечные деформации меньше продольных и редко влияют на работоспособность
детали; при необходимости поперечная деформация рассчитывается через продольную.
где Δα —
поперечное сужение, мм; α0 — начальный поперечный размер, мм.
4. Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяжения (рис. 21.2).
Слайд 8При работе пластические деформации не должны возникать, упругие деформации малы
по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении
материалов проводятся в зоне упругих деформации, где действует закон Гука.На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.
5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.
Слайд 12Занятие 22. (2 часа) Механические испытания, механические характеристики. Предельные и
допускаемые напряжения.
Слайд 1322.1. Механические испытания. Статические испытания на растяжение и сжатие
Это стандартные
испытания: оборудование — стандартная разрывная машина, стандартный образец (круглый или
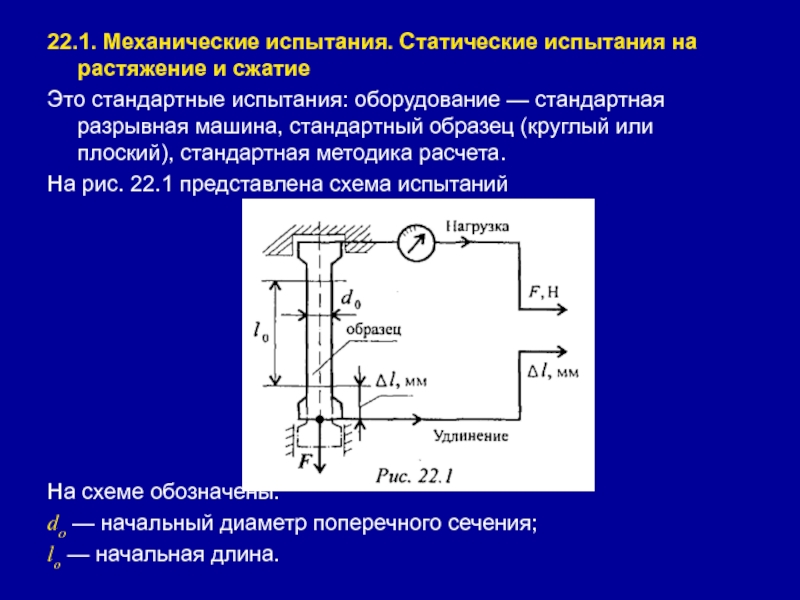
плоский), стандартная методика расчета.На рис. 22.1 представлена схема испытаний
На схеме обозначены:
do — начальный диаметр поперечного сечения;
lо — начальная длина.
Слайд 14На рис. 22.2 изображена схема образца
до (рис. 22.2а) и
после (рис. 22.26) испытаний
dш - диаметр шейки, сужения перед
разрывом.Образец закрепляется в зажимах разрывной машины и растягивается до разрыва.
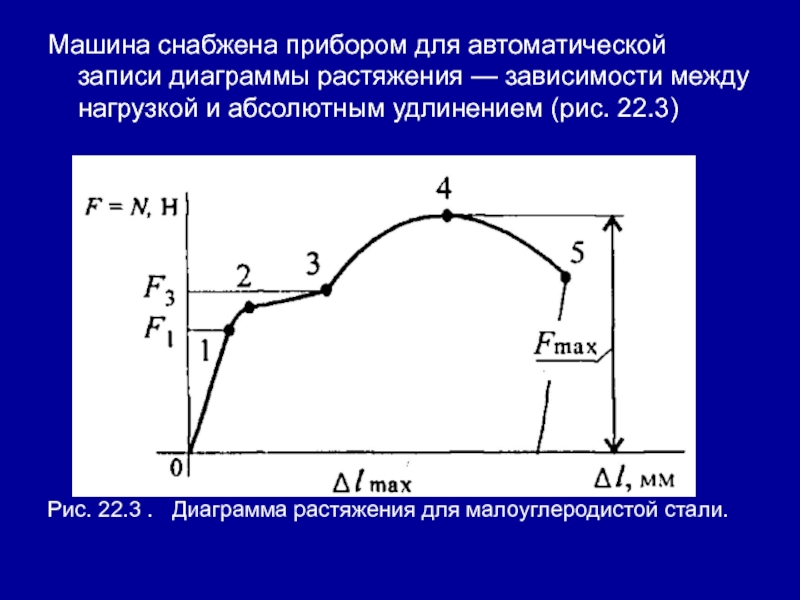
Слайд 15Машина снабжена прибором для автоматической записи диаграммы растяжения — зависимости
между нагрузкой и абсолютным удлинением (рис. 22.3)
Рис. 22.3 .
Диаграмма растяжения для малоуглеродистой стали.Слайд 16Полученная диаграмма пересчитывается и перестраивается (рис. 22.4 — приведенная диаграмма
растяжения первого типа).
Рис.22.4. Приведенная диаграмма растяжения первого типа
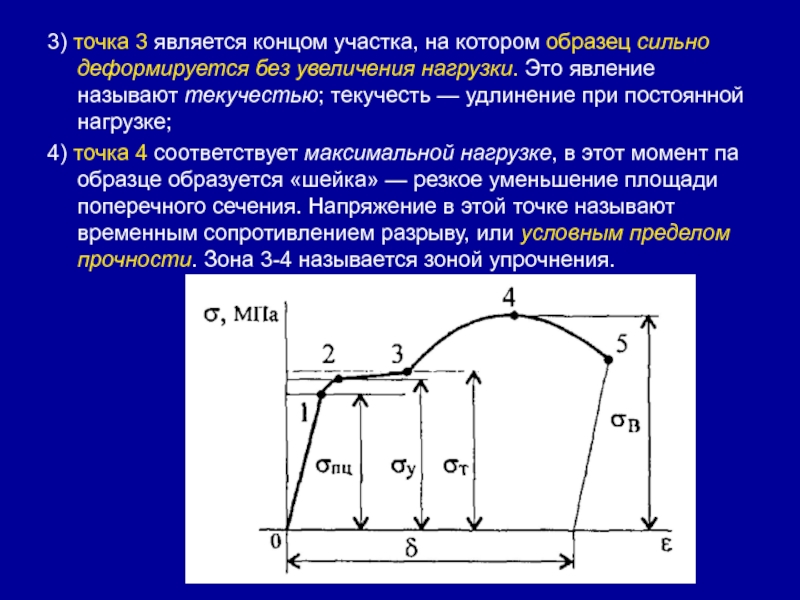
Слайд 171) точка 1 соответствует пределу пропорциональности: после нее прямая линия
(прямая пропорциональность) заканчивается и переходит в кривую;
участок 01 — удлинение
Δl растет пропорционально нагрузке; подтверждается закон Гука;2) точка 2 соответствует пределу упругости материала: материал теряет упругие свойства — способность вернуться к исходным размерам;
Слайд 183) точка 3 является концом участка, на котором образец сильно
деформируется без увеличения нагрузки. Это явление называют текучестью; текучесть —
удлинение при постоянной нагрузке;4) точка 4 соответствует максимальной нагрузке, в этот момент па образце образуется «шейка» — резкое уменьшение площади поперечного сечения. Напряжение в этой точке называют временным сопротивлением разрыву, или условным пределом прочности. Зона 3-4 называется зоной упрочнения.
Слайд 1922.2. Механические характеристики
При построении приведенной диаграммы рассчитываются величины, имеющие условный
характер, усилия в каждой из точек делят на величину начальной
площади поперечного сечения, хотя в каждый момент идет деформация и площадь образца уменьшается.а) Основные характеристики прочности:
1. предел пропорциональности 2.предел упругости
3. предел текучести
4. предел прочности,
или временное сопротивление разрыву,
Где: — начальная площадь сечения.
Слайд 20б) Характеристики пластичности материала
δ — максимальное удлинение в момент разрыва
где
Δl max — максимальное остаточное удлинение (рис. 22.3);
ψ —
максимальное сужение при разрывегде Аш — площадь образца в месте разрыва.
Характеристики пластичности определяют способность материала к деформированию, чем выше значения δ и ψ, тем материал пластичнее.
Слайд 2122.3. Виды диаграмм растяжения
Различные материалы по-разному ведут себя под нагрузкой,
характер деформаций и разрушения зависит от типа материалов.
Принято делить материалы
по типу их диаграмм растяжения на три группы.К первой группе относят пластичные материалы, эти материалы имеют на диаграмме растяжения площадку текучести (диаграммы первого типа) (рис. 22.5а).
Слайд 22Ко второй группе относятся хрупкие материалы, эти материалы мало деформируются,
разрушаются по хрупкому типу. На диаграмме нет площадки текучести (рис.
22.5 б).К третьей группе относят материалы, не имеющие площадку текучести, но значительно деформирующиеся под нагрузкой, их называют пластично-хрупкими
(рис. 22.5в).
Слайд 23Таким образом, хрупкий и пластично-хрупкий материалы не имеют площадки текучести,
а в справочниках отсутствует характеристика «предел текучести». По этой особенности
их можно узнать.Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформацию обычно ограничивают. Максимально возможная относительная деформация ε = 0,2 %.
По величине максимально возможной деформации определяется соответствующее нормальное напряжение σ0,2, которое принимают за предельное.
Слайд 2422.4. Предельные и допустимые напряжения
Предельным напряжением считают напряжение, при котором
в материале возникает опасное состояние (разрушение или опасная деформация).
Для пластичных
материалов предельным напряжением считают предел текучести, т. к. возникающие пластические деформации не исчезают после снятия нагрузки:Для хрупких материалов, где пластические деформации отсутствуют, а разрушение возникает по хрупкому типу (шейки не образуется), за предельное напряжение принимают предел прочности:
Слайд 25Для пластично-хрупких материалов предельным напряжением считают напряжение, соответствующее максимальной деформации
0,2% (σ0,2):
Допускаемое напряжение — максимальное напряжение, при котором материал должен
нормально работать.Допускаемые напряжения получают по предельным с учетом запаса прочности:
где: [σ] — допускаемое напряжение;
s — коэффициент запаса прочности;
[s] — допускаемый коэффициент запаса прочности.
Слайд 26Примечание. В квадратных скобках принято обозначать допускаемое значение величины.
Допускаемый коэффициент
запаса прочности зависит от качества материала, условий работы детали, назначения
детали, точности обработки и расчета и т. д.Он может колебаться от 1,25 для простых деталей до 12,5 для сложных деталей, работающих при переменных нагрузках в условиях ударов и вибраций.
Слайд 2722.5. Расчеты на прочность при растяжении и сжатии
Расчеты на прочность
ведутся по условиям прочности — неравенствам, выполнение которых гарантирует прочность
детали при данных условиях.Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:
Расчетное напряжение σ зависит от нагрузки и размеров поперечного сечения,
допускаемое только от материала детали и условий работы.
Слайд 28Существуют три вида расчета на прочность.
1. Проектировочный расчет — задана
расчетная схема и нагрузки; материал или размеры детали подбираются:
— определение
размеров поперечного сечения:— подбор материала
(по величине σпред можно подобрать марку материала.)
2. Проверочный расчет — известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.
Проверяется неравенство
3. Определение нагрузочной способности (максимальной нагрузки):
Слайд 31Занятие 23. (2 часа) Кручение. Внутренние силовые факторы. Построение эпюр
крутящих моментов.
Расчеты на прочность и жесткость
Слайд 3223.1. Деформации при кручении
Кручение круглого бруса происходит при нагружении его
парами сил с моментами в плоскостях, перпендикулярных продольной оси. При
этом образующие бруса искривляются и разворачиваются на угол γ, называемый углом сдвига (угол поворота образующей).Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения, рис. 23.1).
Длина бруса и размеры поперечного сечения при кручении не изменяются.
рис. 23.1
Слайд 33Связь между угловыми деформациями определяется соотношением
l — длина бруса;
R
— радиус сечения.
Длина бруса значительно больше радиуса сечения, следовательно, φ
>> γ.Угловые деформации при кручении рассчитываются в радианах.
Слайд 3423.2. Гипотезы при кручении
1. Выполняется гипотеза плоских сечений: поперечное сечение
бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским
и перпендикулярным продольной оси.2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).
3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.
Слайд 3523.3. Внутренние силовые факторы при кручении
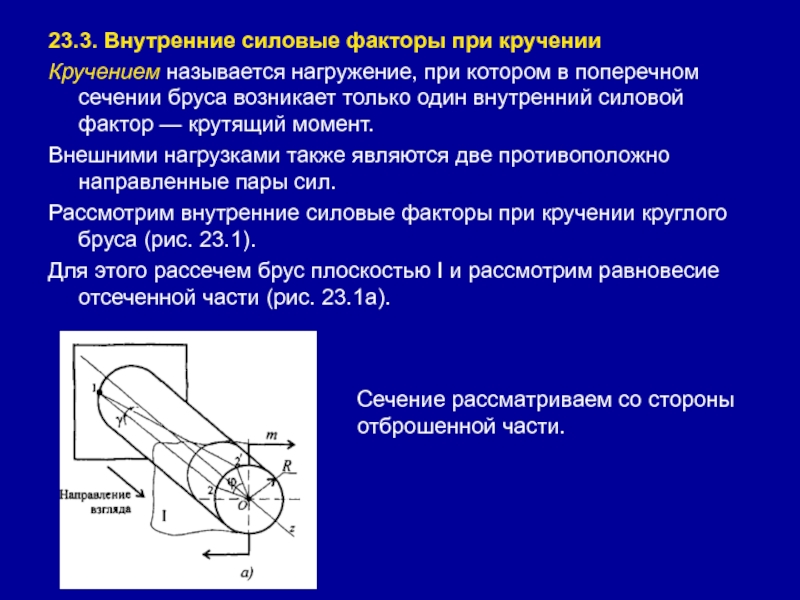
Кручением называется нагружение, при котором
в поперечном сечении бруса возникает только один внутренний силовой фактор
— крутящий момент.Внешними нагрузками также являются две противоположно направленные пары сил.
Рассмотрим внутренние силовые факторы при кручении круглого бруса (рис. 23.1).
Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 23.1а).
Сечение рассматриваем со стороны отброшенной части.
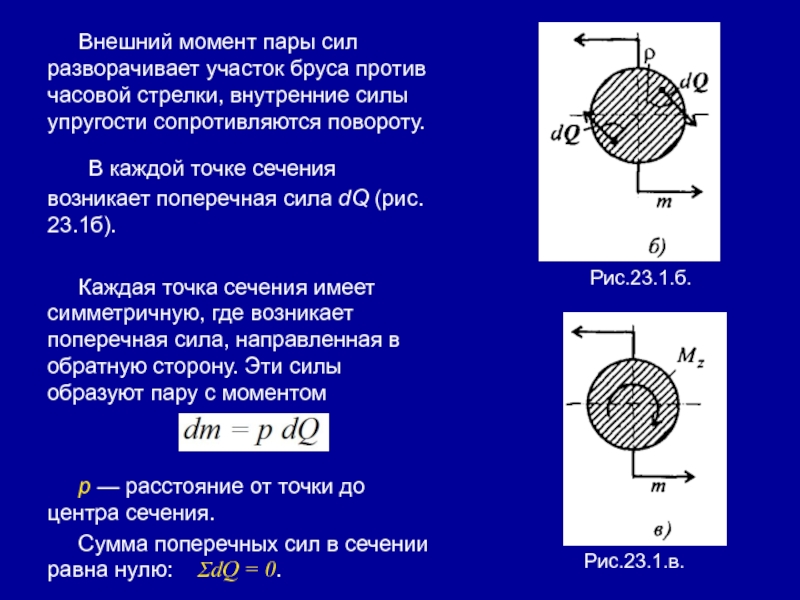
Слайд 36Внешний момент пары сил разворачивает участок бруса против часовой стрелки,
внутренние силы упругости сопротивляются повороту.
В каждой точке сечения возникает
поперечная сила dQ (рис. 23.1б). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом
р — расстояние от точки до центра сечения.
Сумма поперечных сил в сечении равна нулю: ΣdQ = 0.
Рис.23.1.б.
Рис.23.1.в.
Слайд 37С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим
моментом:
Практически крутящий момент определяется из условия равновесия отсеченной части бруса.
Крутящий
момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 23.1в):
Слайд 3823.4. Эпюры крутящих моментов
Крутящие моменты могут меняться вдоль оси бруса.
После определения величин моментов по сечениям строим график-эпюру крутящих моментов
вдоль оси бруса.Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки (рис. 23.2).
Рис. 23.2
Порядок построения эпюры моментов аналогичен построению эпюр продольных сил. Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз, масштаб построения выдерживать обязательно.
Слайд 39Примеры решения задач
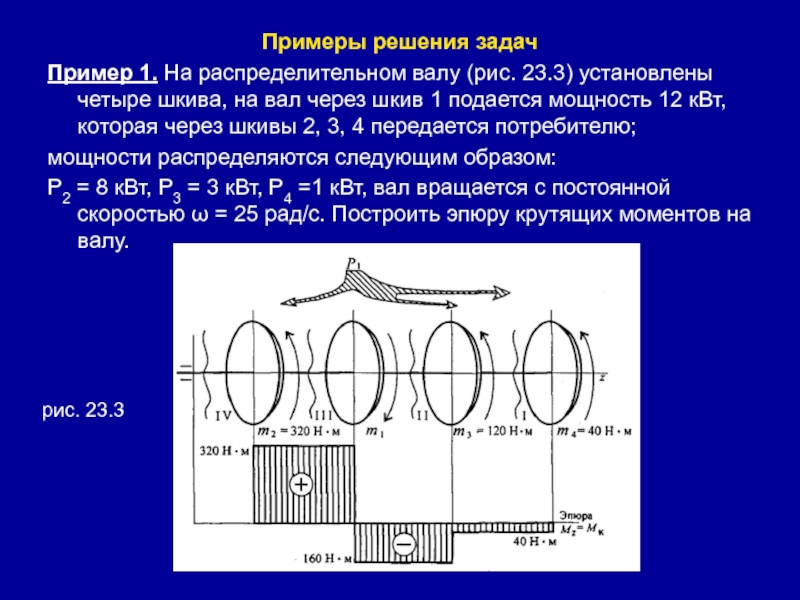
Пример 1. На распределительном валу (рис. 23.3) установлены
четыре шкива, на вал через шкив 1 подается мощность 12
кВт, которая через шкивы 2, 3, 4 передается потребителю;мощности распределяются следующим образом:
P2 = 8 кВт, Р3 = 3 кВт, Р4 =1 кВт, вал вращается с постоянной скоростью ω = 25 рад/с. Построить эпюру крутящих моментов на валу.
рис. 23.3
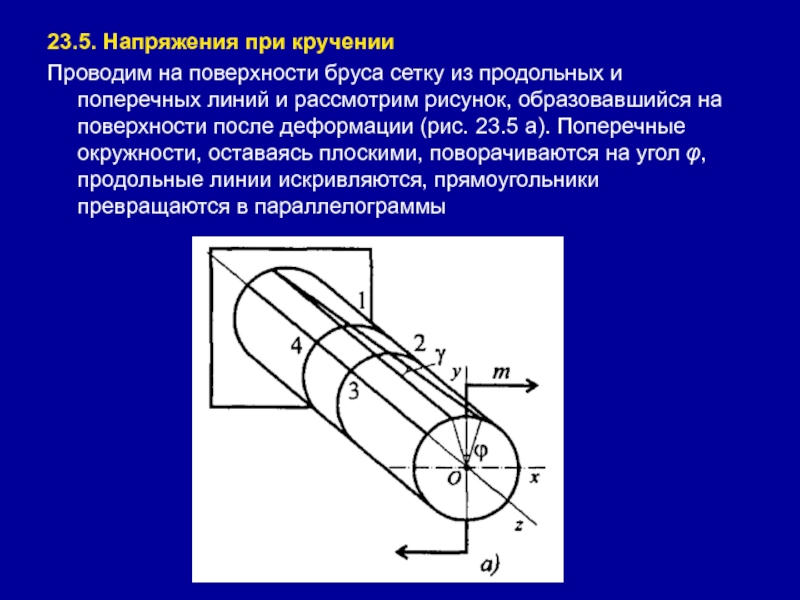
Слайд 4323.5. Напряжения при кручении
Проводим на поверхности бруса сетку из продольных
и поперечных линий и рассмотрим рисунок, образовавшийся на поверхности после
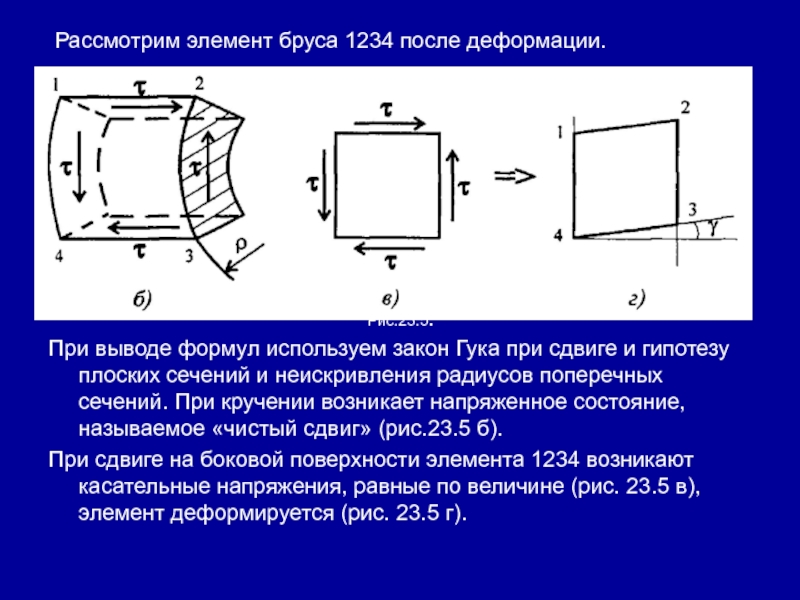
деформации (рис. 23.5 а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ, продольные линии искривляются, прямоугольники превращаются в параллелограммыСлайд 44 Рассмотрим элемент бруса 1234 после деформации.
Рис.23.5.
При выводе формул используем
закон Гука при сдвиге и гипотезу плоских сечений и неискривления
радиусов поперечных сечений. При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис.23.5 б).При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 23.5 в), элемент деформируется (рис. 23.5 г).
Слайд 45Материал подчиняется закону Гука.
Касательное напряжение пропорционально углу сдвига.
Закон Гука
при сдвиге
G — модуль упругости при сдвиге, Н/мм2;
γ
— угол сдвига, рад.Слайд 4623.6. Максимальные напряжения при кручении
Для круглого сечения
Для кольцевого сечения
Где: Wp - момент сопротивления при кручении или полярный момент
сопротивления.d – диаметр бруса круглого сечения.
Слайд 47Условие прочности при кручении
1. Разрушение бруса при кручении происходит с
поверхности, при расчете на прочность используют условие прочности
где [τк] —
допускаемое напряжение крученияСлайд 4823.7. Виды расчетов на прочность
Существует три вида расчетов на прочность:
а) Проектировочный расчет — определяется диаметр бруса [вала) в опасном
сечении:Откуда
б) Проверочный расчет — проверяется выполнение условия прочности
в) Определение нагрузочной способности (максимального крутящего момента)