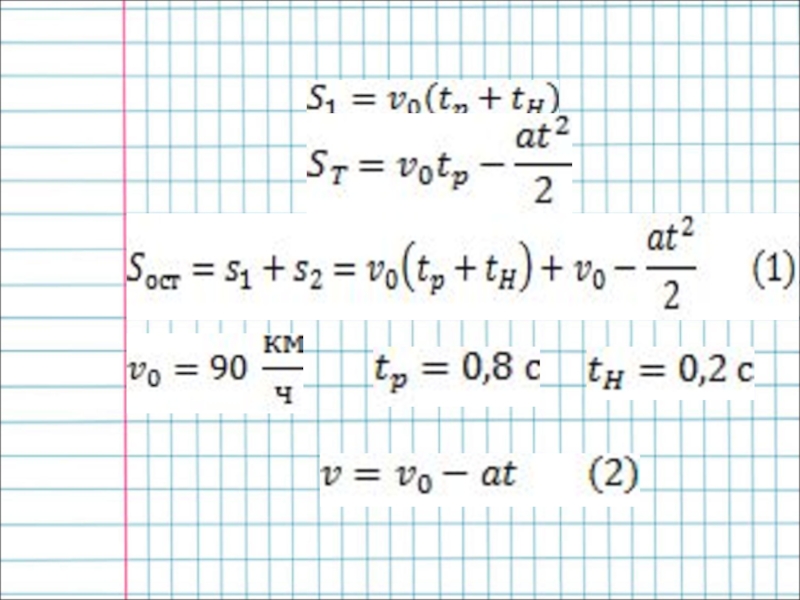Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра, физика и ДТП
Содержание
- 1. Алгебра, физика и ДТП
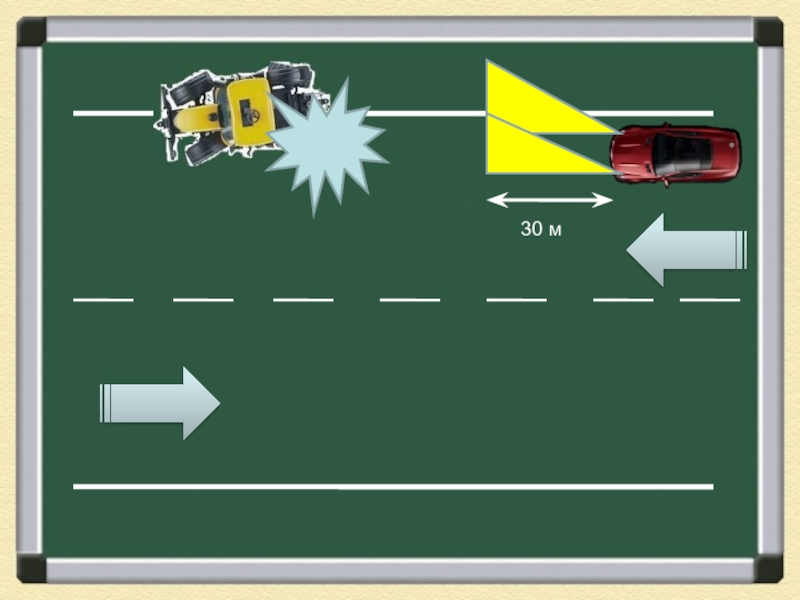
- 2. Задача: Водитель автомобиля «Opel Vectra», двигавшегося ночью по
- 3. 30 м
- 4. Решение:Сформулируем вопрос эксперту на языке физики:“На каком
- 5. Физическая модель движения автомобиля во время торможения-
- 6. tp - время реакции = 0,8 с.tН
- 7. Слайд 7
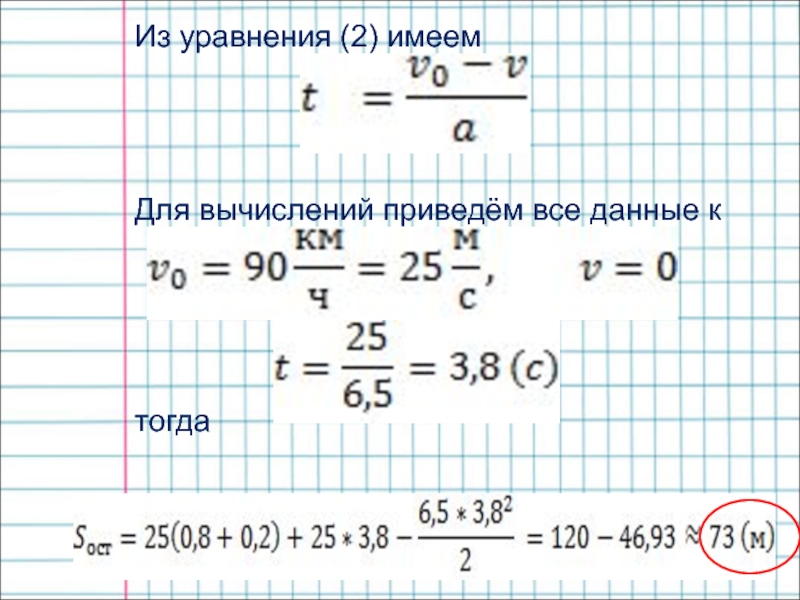
- 8. Из уравнения (2) имеем.Для вычислений приведём все данные к одной системе измерений:тогдаИз уравнения (1) имеем
- 9. Сравнив длину остановочного пути с расстоянием, на
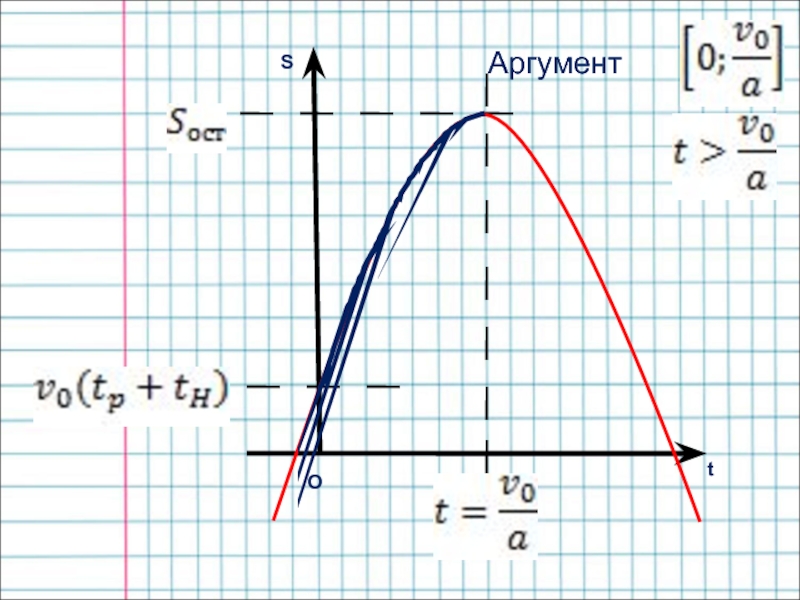
- 10. Рассмотрим графическую иллюстрацию решения данной задачи.Воспользуемся графиком квадратичной функцииВид которой аналогичен виду уравнения
- 11. Независимой переменной в этом случае является время,
- 12. StOАргумент
- 13. Подставив данные задачи в построенную модель, получим
- 14. Скачать презентанцию
Задача: Водитель автомобиля «Opel Vectra», двигавшегося ночью по крайней правой полосе загородного шоссе, совершил наезд на стоявший у обочины трактор. Автомобиль двигался со скоростью 90 км/ч с ближним светом фар. Водитель утверждает,
Слайды и текст этой презентации
Слайд 1Алгебра, физика и ДТП
Математика проникает почти во все отрасли знаний,
являясь «языком» на котором говорят другие науки.
Слайд 2Задача:
Водитель автомобиля «Opel Vectra», двигавшегося ночью по крайней правой полосе
загородного шоссе, совершил наезд на стоявший у обочины трактор. Автомобиль
двигался со скоростью 90 км/ч с ближним светом фар. Водитель утверждает, что применил экстренное торможение, но остановиться не успел. Эксперту задан вопрос: «Имел ли водитель автомобиля возможность избежать столкновения, применив экстренное торможение?»Слайд 4Решение:
Сформулируем вопрос эксперту на языке физики:
“На каком расстоянии автомобиль при
экстренном торможении, т.е при максимально возможном ускорении, может снизить скорость
с 90 км/ч до 0?Больше или меньше это расстояние того, на котором водитель имел возможность увидеть препятствие – стоящий у обочины трактор?”
Слайд 5Физическая модель движения автомобиля во время торможения- равноускоренное движение.
Равноускоренное движение
— движение, при котором ненулевой вектор ускорения остаётся неизменным по
модулю и направлению.Слайд 6tp - время реакции = 0,8 с.
tН - время нарастания
тормозного усилия = 0,2 с.
Во время, складывающееся из времени реакции
и времени нарастания тормозного усилия, движение автомобиля можно считать равномерным.При этом он прошел путь s, за время tp + tН и имел скорость V0.
Пройденный путь равен St.
Равномерное движение — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние
Слайд 8Из уравнения (2) имеем.
Для вычислений приведём все данные к одной
системе измерений:
тогда
Из уравнения (1) имеем
Слайд 9Сравнив длину остановочного пути с расстоянием, на котором водитель мог
обнаружить препятствие, т.е. с дальностью света фар, составляющей 30 метров
при ближнем свете.Вывод: «В сложившейся ситуации водитель не мог избежать наезда с помощью торможения».
Слайд 10Рассмотрим графическую иллюстрацию решения данной задачи.
Воспользуемся графиком квадратичной функции
Вид которой
аналогичен виду уравнения
Слайд 11Независимой переменной в этом случае является время, отсчитываемое от момента
срабатывания тормозной системы – момента начала снижения скорости;
Функция
пройденный путь с
момента начала отсчета
Слайд 13Подставив данные задачи в построенную модель, получим уравнение
Т.к. абсцисса вершины
параболы
Находим ординату вершины
Остановочный путь равен 73 м.
Вывод:
«В сложившейся ситуации водитель не мог избежать наезда с помощью торможения».