Алгоритм Евклида

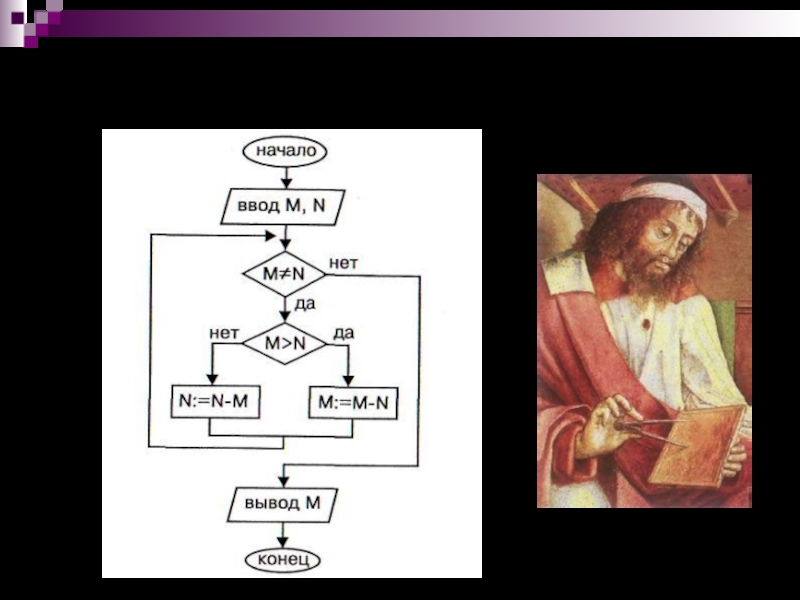
делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух

натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12,18) = 6.
Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М,N).

достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ

решения этой задачи.
Называется он алгоритмом Евклида.

M>N, то
НОД(М,N) = НОД(М - N,N).
Иначе говоря, НОД двух натуральных

чисел равен НОД их положительной разности и меньшего числа.

значит, что М = тК, N = пК, где т,

п — натуральные числа, причем т>п. Тогда М - N = К(т - п), откуда следует, что К — делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их раз­ности M-N, в том числе и наибольший общий делитель. Отсюда:
НОД(М,N) = НОД(М - N,N).
Второе очевидное свойство:
НОД(М,М) = М.

качестве ответа, в противном случае продолжить выполнение алгоритма;
заменить большее число

разностью большего и меньшего из чисел;
вернуться к выполнению п. 1.

общего делителя для двух натуральных чисел

begin
writeln('Введите M и N');
readln(M,N);
while MN do
begin
if M>N

then M:=M-N else N:=N-M
end;
write('HOD=',M)
end.