Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение под углом к горизонту
Содержание
- 1. Движение под углом к горизонту
- 2. Условия задачи Тело брошено со скоростью V
- 3. Дано:V, @Решение:Найти:1)Уравнения движения2) t3) l4) H max5) V6) a , a t7) R
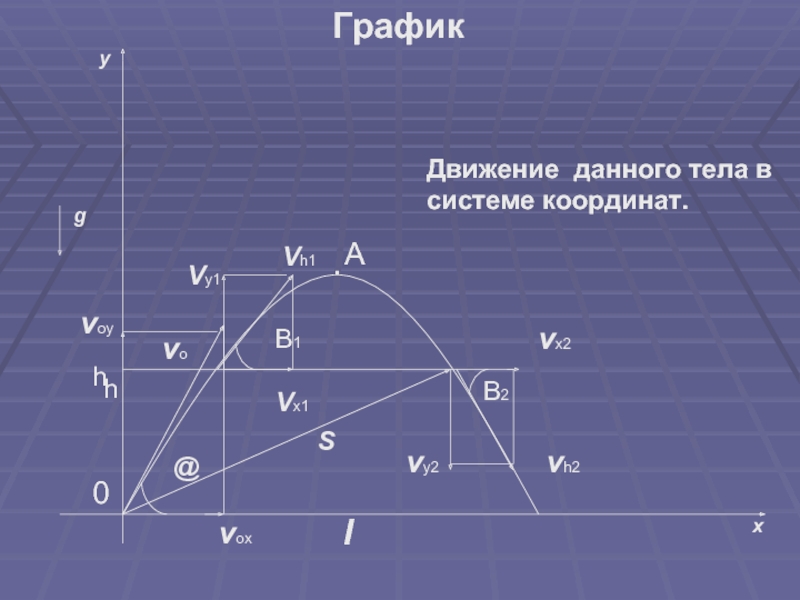
- 4. yxgvoyvox@lSvovx2vh2vy2B1B2Движение данного тела в системе координат.ГрафикА.0hhVh1Vy1Vx1
- 5. Решение Движение тела вдоль
- 6. Найти траекторию движения – это значит найти
- 7. 3) Т. к. вдоль оси x движение
- 8. 5) Для определения скорости на высоте h
- 9. Модуль скорости равен Vh 1 = V0^2-2gh,
- 10. 6)В точке О a0
- 11. ПриложениеОзнакомившись с основными действиями пи решении задач
- 12. Условия задачиТело брошено горизонтально со скоростью 20м/с.Определить
- 13. Если у Вас возникли трудности при решении
- 14. Этапы решения1.Выбрать оси координат.2.Записать уравнения движения тела.3.Определить
- 15. Формулы
- 16. ОтветS = 45 м.
- 17. Спасибо за
- 18. Скачать презентанцию
Условия задачи Тело брошено со скоростью V под углом @ к горизонту. Определить:Траекторию движения телаВремя полёта Дальность полётаМаксимальную высоту подъёма HСкорость тела на высоте h
Слайды и текст этой презентации
Слайд 2Условия задачи
Тело брошено со скоростью V под углом @
к горизонту. Определить:
Траекторию движения тела
Время полёта
Дальность полёта
Максимальную высоту подъёма
HСкорость тела на высоте h
Радиусы кривизны в этих точках
Слайд 5Решение
Движение тела вдоль оси x равномерное(ax=0);V0x
= Vocos@, причем Vx=V0x=const. Уравнение движения вдоль оси x имеет
вид:x = x0xt = v0xtcos@
Движение по оси y равнопеременное с ускорением ау = -g = const и начальной скоростью Voy = V0sin@; Vy = Voy – gt.
Уравнение движения вдоль оси у имеет вид:
y = Voyt – gt^2/2 = V0tsin@ - gt^2/2
Слайд 6
Найти траекторию движения – это значит найти аналитическое уравнение кривой,
по которой движется тело в пространстве. Т. к.
t = x/V0cos@ , тоy = xtg@ - gx^2/2V0^2cos^2@ .
2. Найдём t ,приравняв y = V0tsin@ - gt^2/2 к 0:
t(V0sin@ - gt/2) = 0
t1=0 t2 = (2V0/g)sin@
Действительно, тело на земле оказывается дважды - в начале и в конце полёта.
Слайд 73) Т. к. вдоль оси x движение равномерное и известно
время движения, то
xmax = l = V0xt =
(V0cos@2V0sin@)/g = =V0^2sin2@/g4) Hmax можно найти через время подъёма tпод. Т. к. в точке Нmax Vy=0, то
0 = V0y – gtпод
tпод = (V0/g)sin@
Таким образом,
Ymax = Hmax = V0ytпод – V0yt под ^2/2 = V0y^2/2g
Hmax = (V0^2sin^2@)/2g.
Слайд 85) Для определения скорости на высоте h необходимо знать время,
когда тело находиться на этой высоте, th
Vx = V0x, Vy = V0y – gth y = h = V0yth – gth^2/2
(th)1,2 = V0y+/- V0y^2 – 2gh
g
Скорость в первой точке при th1
Vx1 = V0cos@
Vy1 = (V0^2sin^2@ - 2gh)
Слайд 9Модуль скорости равен Vh 1 = V0^2-2gh,
тангенс угла наклона
скорости к оси х:
tgB1=Vy1/Vx1 =
V0^2sin^2@ – 2ghV0cos@
Скорость во второй точке при th2
Vx2 = V0cos@
Vy2 = - V0^2sin^2@ - 2gh
Модуль скорости равен Vh 2 = V0^2-2gh,
тангенс угла наклона скорости к оси х:
tgB1=Vy1/Vx1 = - V0^2sin^2@ – 2gh
V0cos@
Слайд 106)В точке О
a0 = -gcos@
а0t =
-gsin@В точке А
аА = -g atA = 0
7)Нормальное ускорение определяется по формуле
а = V^2/R R = V^2/a, где R – радиус кривизны в данной точке, т. е. радиус окружности, часть дуги которой совпадает с траекторией в данной точке.
В точке О
V = V0, a = gcos@
R0 = V0^2/gcos@
B точке А
Vy = 0, a = g, VA = V0x = V0cos@
RA = (V0^2cos@)/g
Слайд 11Приложение
Ознакомившись с основными действиями пи решении задач по теме «Движение
под углом к горизонту», Вы можете проверить приобретенные знания. С
этой целью Вам предлагается следующая задача:Слайд 12Условия задачи
Тело брошено горизонтально со скоростью 20м/с.Определить смещение тела от
точки бросания,S, при котором скорость будет направлена под углом 45’
к горизонту.Слайд 13
Если у Вас возникли трудности при решении задачи, Вы можете
воспользоваться следующими подсказками:
1)Кратко изложенные этапы решения;
2)Необходимые формулы;
3)Ответ.
Слайд 14Этапы решения
1.Выбрать оси координат.
2.Записать уравнения движения тела.
3.Определить момент времени t,
когда скорость будет направлена под углом 45’ к горизонту.
4.Подставить t
в уравнение движения и найти координаты тела.5.Найти искомое перемещение.
Теги