Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярная физика и основы термодинамики
Содержание
- 1. Молекулярная физика и основы термодинамики
- 2. Основные газовые законыЗакон Дальтона: Закон Бойля-Мариотта: P⋅V=const
- 3. Основные газовые законыЗаконы Шарля и Гей-Люссака имеют
- 4. Основные газовые законыПроцессы, описываемые уравнениями 2-4 называются изопроцессами:ИзотермическимИзохорнымИзобарным
- 5. Изотермический процесс
- 6. Изотермический процесс
- 7. Изохорный процесс
- 8. Изохорный процесс
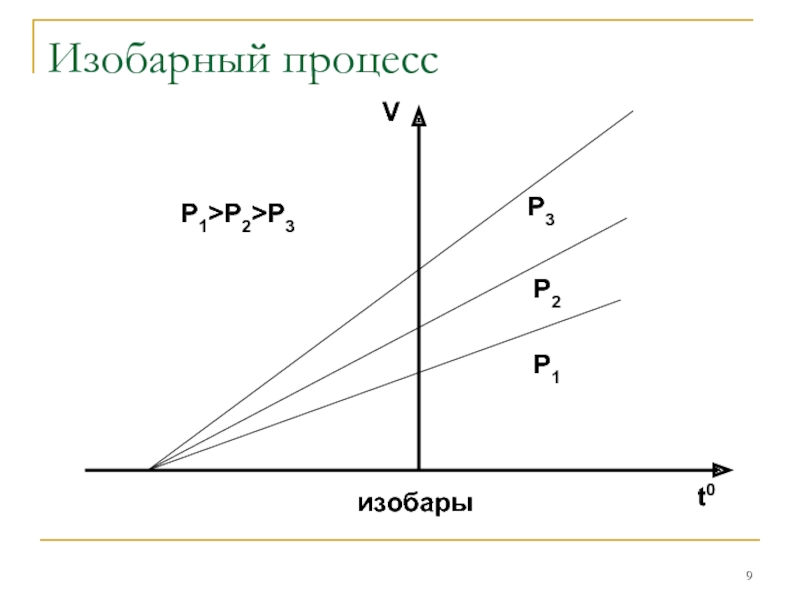
- 9. Изобарный процесс
- 10. Изобарный процесс
- 11. Основные газовые законыЕсли измерять температуру по шкале
- 12. Основные газовые законыЕсли ввести новую шкалу температур,
- 13. Основные газовые законыРассмотрим переход из состояния 1
- 14. Основные газовые законыИз закона Авогадро следует, что
- 15. Основные газовые законыТ.о., мы пришли к уравнению Клапейрона-Менделеева: P⋅V=ν⋅R⋅T или P⋅V=(m/μ)⋅R⋅T
- 16. Основные газовые законыИдеальный газИдеальным называется такой газ,
- 17. Кинетическая теория газовОценка размеров молекулСредний размер молекул
- 18. Кинетическая теория газовОценка расстояния между молекулами в
- 19. Кинетическая теория газовОценка средней длины свободного пробега
- 20. Кинетическая теория газовЗадача МКТ заключается в установлении
- 21. Вывод основного уравнения МКТРассмотрим цилиндр с площадью
- 22. Вывод основного уравнения МКТЧисло ударов о стенку:
- 23. Вывод основного уравнения МКТ→ P=ΣFi/S=Σni⋅vix⋅ pix=n⋅=1/3⋅n⋅ ⋅=(2/3)⋅n⋅Таким образом мы получили основное уравнение молекулярно-кинетической теории газов: Р=(2/3)⋅n⋅
- 24. Оценка скорости молекулР=(2/3)⋅n⋅=(2/3)⋅n⋅m⋅/2= =N⋅m⋅/(3⋅V)=M⋅/(3⋅V) → → =3⋅P⋅V/M=3⋅P/ρ →
- 25. Оценка скорости молекулДля молекул водорода Н2 μ=2⋅10-3
- 26. Кинетическая теория газовСравнивая уравнение Клапейрона-Менделеева: P=ν⋅R⋅T/V, где
- 27. Кинетическая теория газовОкончательно получаем: =(3/2)⋅k⋅T где k –
- 28. Кинетическая теория газовИз Р=(2/3)⋅n⋅ и =(3/2)⋅k⋅T следует что: P=n⋅k⋅T
- 29. Конец лекции
- 30. Скачать презентанцию
Основные газовые законыЗакон Дальтона: Закон Бойля-Мариотта: P⋅V=const при t0=constЗакон Шарля: P/T=const при V=constЗакон Гей-Люссака: V/T=const при P=constЗакон Авогадро: одинаковые количества газов при одинаковых температуре и давлении занимают
Слайды и текст этой презентации
Слайд 1Лекции по физике. Молекулярная физика и основы термодинамики
Основные газовые законы.
Идеальный газ. Кинетическая теория газов
Слайд 2Основные газовые законы
Закон Дальтона:
Закон Бойля-Мариотта: P⋅V=const при t0=const
Закон Шарля:
P/T=const при V=const
Закон Гей-Люссака: V/T=const при
P=constЗакон Авогадро: одинаковые количества газов при одинаковых температуре и давлении занимают одинаковый объём
Слайд 3Основные газовые законы
Законы Шарля и Гей-Люссака имеют такой простой вид
если температура измеряется по абсолютной шкале
Первоначально эти законы были сформулированы
для температуры, измеренной в некоторой практической шкале. В этом случае они имеют более сложный вид:P=P0[1+α⋅(t-t0)]
V=V0[1+β⋅(t-t0)]
при чём коэффициенты α и β оказались равными и не зависящими от рода газа
Слайд 4Основные газовые законы
Процессы, описываемые уравнениями
2-4 называются изопроцессами:
Изотермическим
Изохорным
Изобарным
Слайд 11Основные газовые законы
Если измерять температуру по шкале Цельсия, то оказывается,
что точка пересечения изохорного и изобарного процессов с осью температур
имеет координату t=-373,15 0С. Это значит, что α=β=1/273,15 1/0ССлайд 12Основные газовые законы
Если ввести новую шкалу температур, такую, что Т=t+273,15,
то уравнения примут более простой вид:
P/T=const
V/T=const
Определённая таким образом температура называется
абсолютной температуройСлайд 13Основные газовые законы
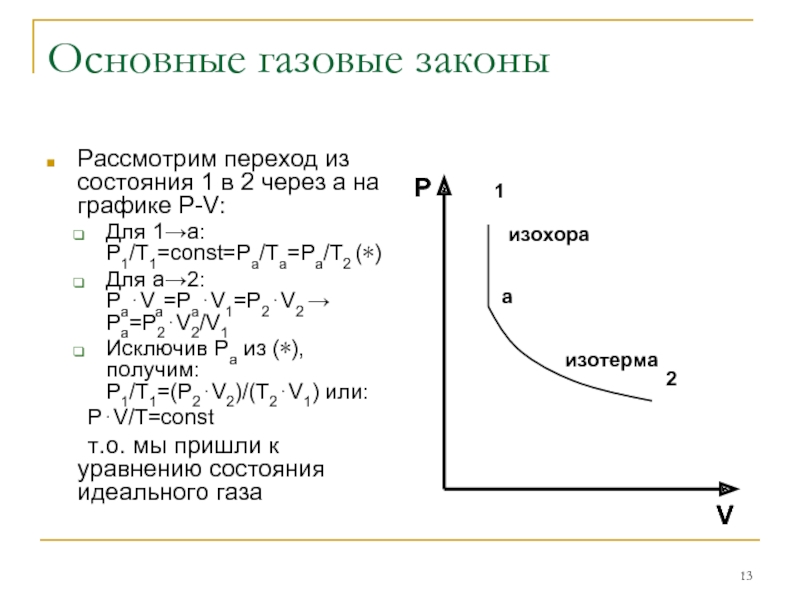
Рассмотрим переход из состояния 1 в 2 через
а на графике P-V:
Для 1→а: P1/T1=const=Pa/Ta=Pa/T2 (∗)
Для а→2: Pa⋅Va=Pa⋅V1=P2⋅V2 →
Pa=P2⋅V2/V1Исключив Ра из (∗), получим: P1/T1=(P2⋅V2)/(T2⋅V1) или:
P⋅V/T=const
т.о. мы пришли к уравнению состояния идеального газа
Слайд 14Основные газовые законы
Из закона Авогадро следует, что величина соотношения (P⋅V)/T
не зависит от вида газа, значит мы можем записать, что
для одного моля любого газа (P⋅V)/T=R, где R – универсальная газовая постоянная, называемая постоянной АвогадроR=8,31 Дж/(град⋅моль)
Из закона Дальтона следует, что при постоянных V и Т, Р является линейной функцией количества вещества ν
Слайд 15Основные газовые законы
Т.о., мы пришли к уравнению Клапейрона-Менделеева:
P⋅V=ν⋅R⋅T
или
P⋅V=(m/μ)⋅R⋅T
Слайд 16Основные газовые законы
Идеальный газ
Идеальным называется такой газ, который подчиняется закону
Клапейрона-Менделеева
Поведение реальных газов приближается к поведению идеального газа в пределе
низких давлений и высоких температурРазмеры молекул идеального газа малы по сравнению с межмолекулярным расстоянием, а энергией взаимодействия молекул можно пренебречь
Слайд 17Кинетическая теория газов
Оценка размеров молекул
Средний размер молекул =(V/N)1/3, где V
– объём, а N – количество молекул
Для воды: ρ=1г/см3, μ=18
г/моль → Vμ=18 см3. =3⋅10-10 м
Слайд 18Кинетическая теория газов
Оценка расстояния между молекулами в газе
=(V/NA)1/3, при
комнатной температуре и атмосферном давлении 1 моль газа занимает объём
22 400 см3 →<>=(22400/6⋅1023)1/3≈3,3⋅10-7 см
Т.о. <> на порядок больше, чем
Слайд 19Кинетическая теория газов
Оценка средней длины свободного пробега молекул в газах
λ∼⋅(/)2
При
нормальном давлении λ∼10-5 см, то есть на два порядка больше
<>Слайд 20Кинетическая теория газов
Задача МКТ заключается в установлении взаимосвязи между макроскопическими
параметрами ТД системы (P, T и др.) и её микроскопическими
характеристиками (λ, μ,Слайд 21Вывод основного уравнения МКТ
Рассмотрим цилиндр с площадью основания S=1, опирающийся
на стенку сосуда
Примем следующую модель
Частицы разделены на три равные группы,
каждая из которых движется вдоль одной из координатных осейЧастицы не взаимодействуют между собой
При ударе частицы о стенку, на неё действует сила
Слайд 22Вывод основного уравнения МКТ
Число ударов о стенку:
zi=S⋅ni⋅vix⋅Δt
Заменим в (∗)
i на так, что i⋅τ= ⋅Δt
Тогда, полная сила, действующая
на стенку со стороны молекул, имеющих скорость vix:Fix=zi⋅2⋅ pix/Δt=S⋅ni⋅vix⋅ pix
Слайд 23Вывод основного уравнения МКТ
→ P=ΣFi/S=Σni⋅vix⋅ pix=n⋅=1/3⋅n⋅
⋅=(2/3)⋅n⋅
Таким образом мы получили
основное уравнение молекулярно-кинетической теории газов:
Р=(2/3)⋅n⋅
Слайд 25Оценка скорости молекул
Для молекул водорода Н2 μ=2⋅10-3 кг/моль,
при комнатной температуре:
≈1800 м/с
для молекул О2 μ=2⋅10-3 кг/моль, при комнатной температуре:
≈500 м/с
Слайд 26Кинетическая теория газов
Сравнивая уравнение Клапейрона-Менделеева:
P=ν⋅R⋅T/V, где ν/V=n/Na
с основным
уравнением молекулярно-кинетической теории газов:
Р=(2/3)⋅n⋅
мы можем заключить что:
R⋅T/NA=(2/3)⋅
Слайд 27Кинетическая теория газов
Окончательно получаем:
=(3/2)⋅k⋅T
где k – постоянная Больцмана
k=1,38⋅10-23 Дж/град
k=R/NA
Т.о.
мы выяснили молекулярно-кинетический смысл температуры – она пропорциональна средней кинетической
энергии молекулы
Теги