Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поляризация света
Содержание
- 1. Поляризация света
- 2. Поляризация светаВ начале XIX века, когда Т.
- 3. Однако, постепенно накапливались экспериментальные факты, свидетельствующие в
- 4. В 1809 году французский инженер Э. Малюс
- 5. Интенсивность прошедшего света оказалась прямо пропорциональной cos2
- 6. Таким образом, асимметрия относительно луча является решающим
- 7. В электромагнитной волне вектора и
- 8. Если вдоль одного и того же направления
- 9. В эллиптически-поляризованной волне в любой плоскости P,
- 10. Рис. 3.11.5 дает представление о пространственной структуре эллиптически-поляризованной волны.Рисунок 3.11.5.Электрическое поле в эллиптически-поляризованной волне.
- 11. Линейно-поляризованный свет испускается лазерными источниками. Свет может
- 12. В каждый момент времени вектор может быть
- 13. Это означает, что любую волну (поляризованную и
- 14. У многих кристаллов поглощение света сильно зависит
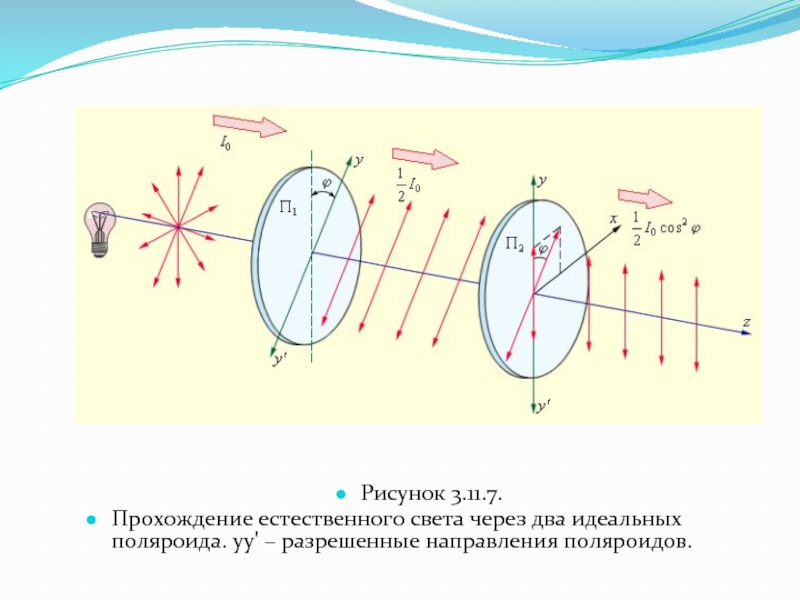
- 15. Рисунок 3.11.7.Прохождение естественного света через два идеальных поляроида. yy' – разрешенные направления поляроидов.
- 16. Если обозначить амплитуду линейно-поляризованной волны после прохождения
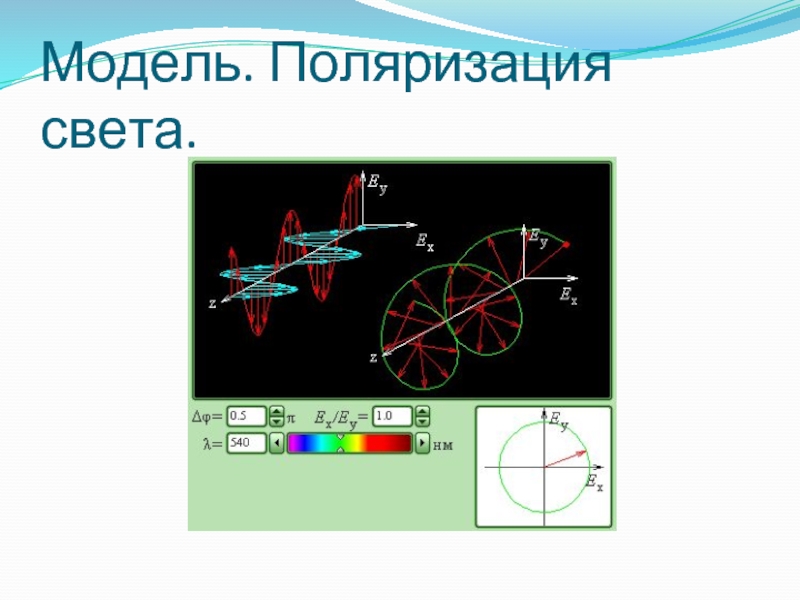
- 17. Модель. Поляризация света.
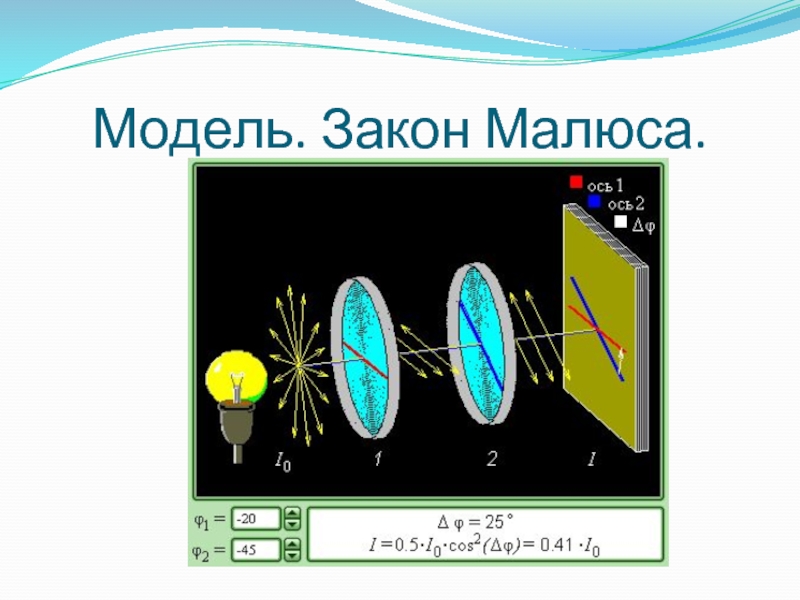
- 18. Модель. Закон Малюса.
- 19. Спасибо за внимание!!!!!!!
- 20. Скачать презентанцию
Слайды и текст этой презентации
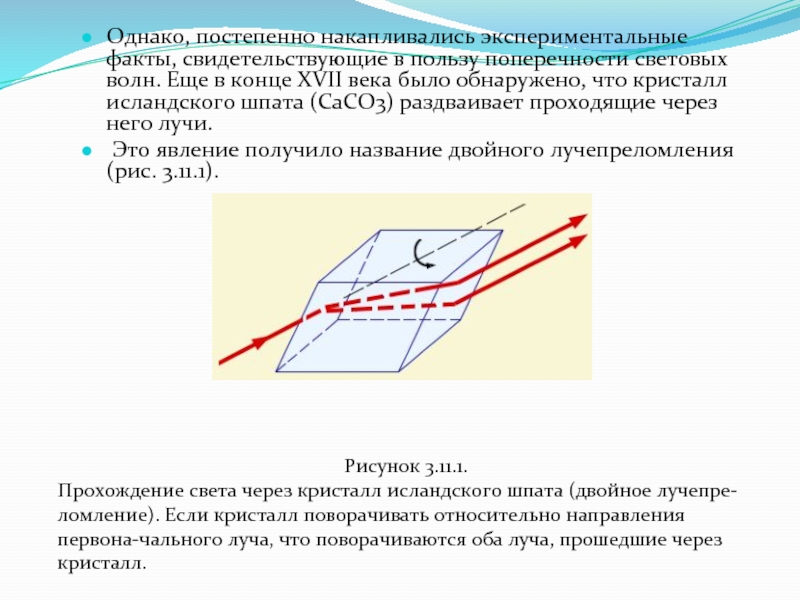
Слайд 3Однако, постепенно накапливались экспериментальные факты, свидетельствующие в пользу поперечности световых
волн. Еще в конце XVII века было обнаружено, что кристалл
исландского шпата (CaCO3) раздваивает проходящие через него лучи.Это явление получило название двойного лучепреломления (рис. 3.11.1).
Рисунок 3.11.1.
Прохождение света через кристалл исландского шпата (двойное лучепре-ломление). Если кристалл поворачивать относительно направления первона-чального луча, что поворачиваются оба луча, прошедшие через кристалл.
Слайд 4В 1809 году французский инженер Э. Малюс открыл закон, названный
его именем. В опытах Малюса свет последовательно пропускался через две
одинаковые пластинки из турмалина (прозрачное кристаллическое вещество зеленоватой окраски). Пластинки могли поворачиваться друг относительно друга на угол φ (рис. 3.11.2).Рисунок 3.11.2.
Иллюстрация к закону Малюса
Слайд 5Интенсивность прошедшего света оказалась прямо пропорциональной cos2 φ:
Ни двойное лучепреломление,
ни закон Малюса не могут найти объяснение в рамках теории
продольных волн. Для продольных волн направление распространения луча является осью симметрии. В продольной волне все направления в плоскости, перпен-дикулярной лучу, равноправны. В поперечной волне (например, в волне, бегущей по резиновому жгуту) направление колебаний и перпендикулярное ему направление не равноправны (рис. 3.11.3).I ~ cos2 φ
Рисунок 3.11.3.
Поперечная волна в резиновом жгуте. Частицы колеблются вдоль оси y. Поворот щели S вызовет затухание волны.
Слайд 6Таким образом, асимметрия относительно луча является решающим признаком, который отличает
поперечную волну от продольной. Впервые догадку о поперечности световых волн
высказал Т. Юнг (1816 г.). Френель, независимо от Юнга, также выдвинул концепцию поперечности световых волн, обосновал ее многочисленными экспериментами и создал теорию двойного лучепреломления света в кристаллах.В середине 60-х годов XIX века Максвелл сделал вывод о том, что свет – это электромагнитные волны. Этот вывод был сделан на основе совпадения известного значения скорости света со скоростью распространения предсказанных Максвеллом электромагнитных волн. К тому времени, когда Максвелл сделал вывод о существовании электромагнитных волн, поперечность световых волн уже была доказано экспериментально. Поэтому Максвелл справедливо полагал, что поперечность электромагнитных волн является еще одним важнейшим доказательством электромагнитной природы света.
В электромагнитной теории света исчезли все затруднения, связанные с необходимостью введения особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело.
Слайд 7В электромагнитной волне вектора и перпендикулярны друг другу
и лежат в плоскос-ти, перпендикулярной направлению распростра-нения волны . Во
всех процессах взаимодействия света с веществом основную роль играет элек-трический вектор поэтому его называют свето-вым вектором. Если при распространении элек-тромагнитной волны световой вектор сохраняет свою ориентацию, такую волну называют линейно-поляризованной или плоско-поляризо-ванной (термин поляризация волн был введен Малюсом применительно к поперечным механическим волнам). Плоскость, в которой колеблется световой вектор называется плоскостью колебаний, а плоскость, в которой совершает колебание магнитный вектор – плоскостью поляризации.Слайд 8Если вдоль одного и того же направления распространяются две монохроматические
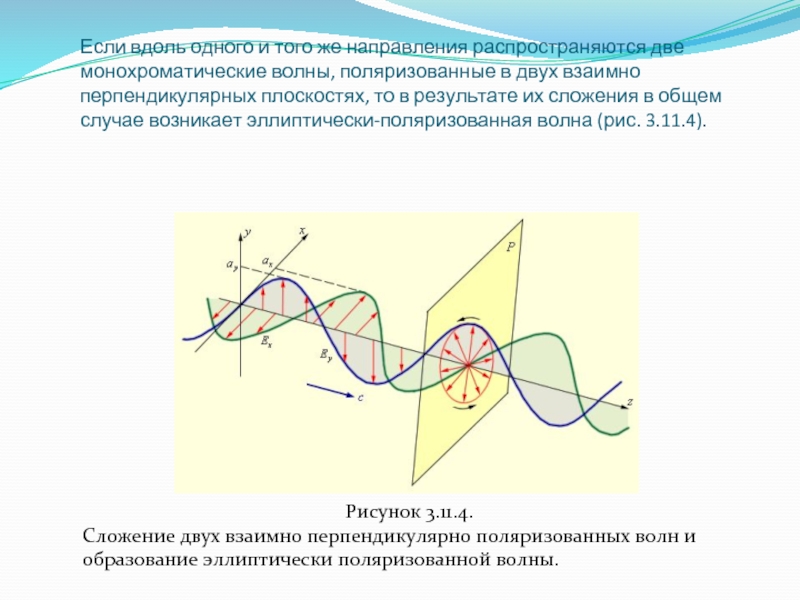
волны, поляризованные в двух взаимно перпендикулярных плоскостях, то в результате
их сложения в общем случае возникает эллиптически-поляризованная волна (рис. 3.11.4).Рисунок 3.11.4.
Сложение двух взаимно перпендикулярно поляризованных волн и образование эллиптически поляризованной волны.
Слайд 9В эллиптически-поляризованной волне в любой плоскости P, перпендикулярной направлению распространения
волны, конец результирующего вектора за один период
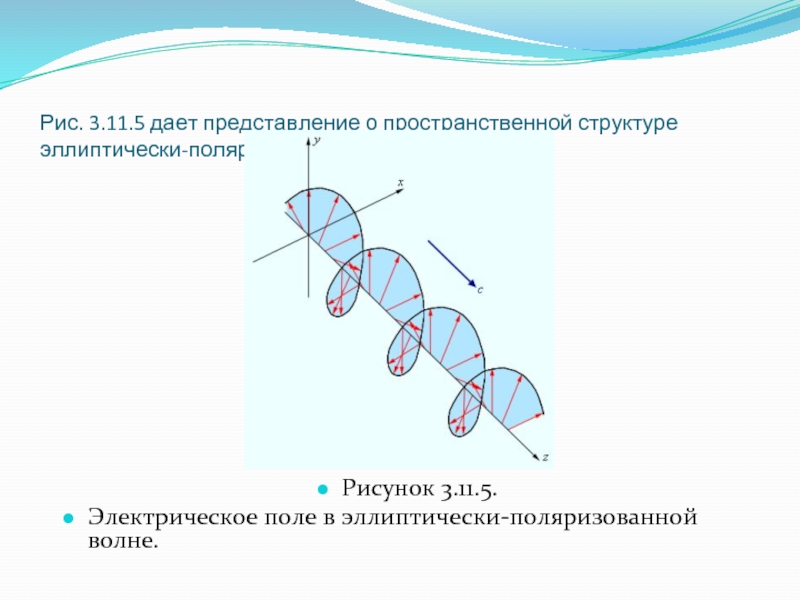
светового колебания обегает эллипс, который называется эллипсом поляризации. Форма и размер эллипса поляризации определяются амплитудами ax и ay линейно-поляризован-ных волн и фазовым сдвигом Δφ между ними. Частным случаем эллиптически-поляризован-ной волны является волна с круговой поляри-зацией (ax = ay, Δφ = ± π / 2).Слайд 10Рис. 3.11.5 дает представление о пространственной структуре эллиптически-поляризованной волны.
Рисунок 3.11.5.
Электрическое
поле в эллиптически-поляризованной волне.
Слайд 11Линейно-поляризованный свет испускается лазерными источниками. Свет может оказаться поляризованным при
отражении или рассеянии. В частности, голубой свет от неба частично
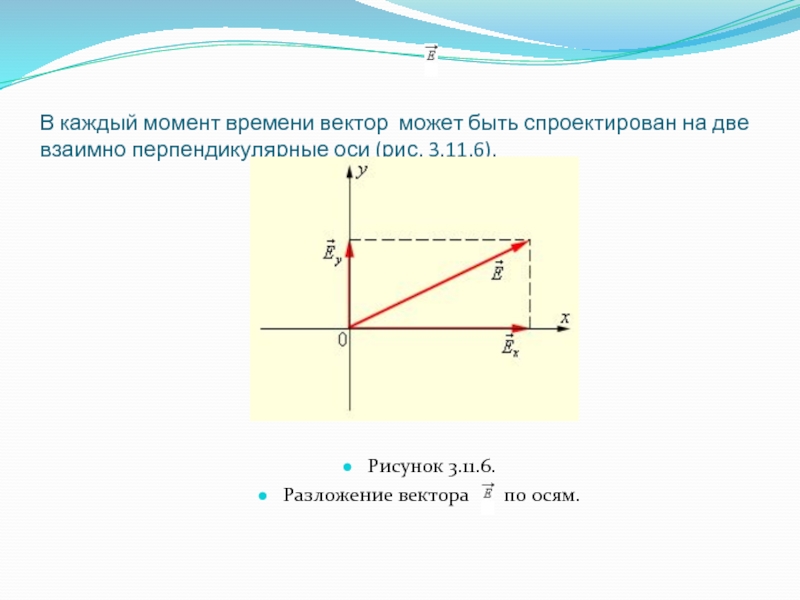
или полностью поляризован. Однако, свет, испускаемый обычными источниками (например, солнечный свет, излучение ламп накаливания и т. п.), неполяризован. Свет таких источников состоит в каждый момент из вкладов огромного числа независимо излучающих атомов с различной ориентацией светового вектора в излуча-емых этими атомами волнах. Поэтому в результиру-ющей волне вектор беспорядочно изменяет свою ориентацию во времени, так что в среднем все направления колебаний оказываются равноправными. Неполяризованный свет называют также естественным светом.Слайд 12В каждый момент времени вектор может быть спроектирован на две
взаимно перпендикулярные оси (рис. 3.11.6).
Рисунок 3.11.6.
Разложение вектора
по осям.Слайд 13Это означает, что любую волну (поляризованную и неполяризованную) можно представить
как суперпозицию двух линейно-поляризованных во взаимно перпендикулярных направлениях волн:
Но в поляризованной волне обе составляющие Ex(t) и Ey(t) когерентны, а в неполяризованной – некогерентны, т. е. в первом случае разность фаз между Ex(t) и Ey(t) постоянна, а во втором она является случайной функцией времени.Явление двойного лучепреломления света объясняется тем, что во многих кристаллических веществах показатели преломления для двух взаимно перпендикулярно поляризованных волн различны. Поэтому кристалл раздваивает проходящие через него лучи (рис. 3.11.1). Два луча на выходе кристалла линейно поляризованы во взаимно перпендикулярных направлениях. Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными.
С помощью разложения вектора на составляющие по осям можно объяснить закон Малюса
Слайд 14У многих кристаллов поглощение света сильно зависит от направления электрического
вектора в световой волне. Это явление называют дихроизмом. Этим свойством,
в частности, обладают пластины турмалина, использованные в опытах Малюса. При определенной толщине пластинка турмалина почти полностью поглощает одну из взаимно перпендикулярно поляризованных волн (например, Ex) и частично пропускает вторую волну (Ey). Направление колебаний электрического вектора в прошедшей волне называется разрешенным направлением пластинки. Пластинка турмалина может быть использована как для получения поляризованного света, так и для анализа характера поляризации света (поляризатор и анализатор). В настоящее время широко применяются искусственные дихроичные пленки, которые называются поляроидами. Поляроиды почти полностью пропускают волну разрешенной поляризации и не пропускают волну, поляризованную в перпендикулярном направлении. Таким образом, поляроиды можно считать идеальными поляризационными фильтрами.Рассмотрим прохождение естественного света последовательно через два идеальных поляроида П1 и П2 (рис. 3.11.7), разрешенные направления которых развернуты на некоторый угол φ. Первый поляроид играет роль поляризатора. Он превращает естественный свет в линейно-поляризованный. Второй поляроид служит для анализа падающего на него света.
Слайд 15Рисунок 3.11.7.
Прохождение естественного света через два идеальных поляроида. yy' –
разрешенные направления поляроидов.
Слайд 16Если обозначить амплитуду линейно-поляризованной волны после прохождения света через
первый поляроид
через то волна, пропущенная вторым поляроидом, будет иметь амплитуду E = E0 cos φ. Следовательно, интенсивность I линейно-поляризованной волны на выходе второго поляроида будет равнаТаким образом, в электромагнитной теории света закон Малюса находит естественное объяснение на основе разложения вектора на составляющие.