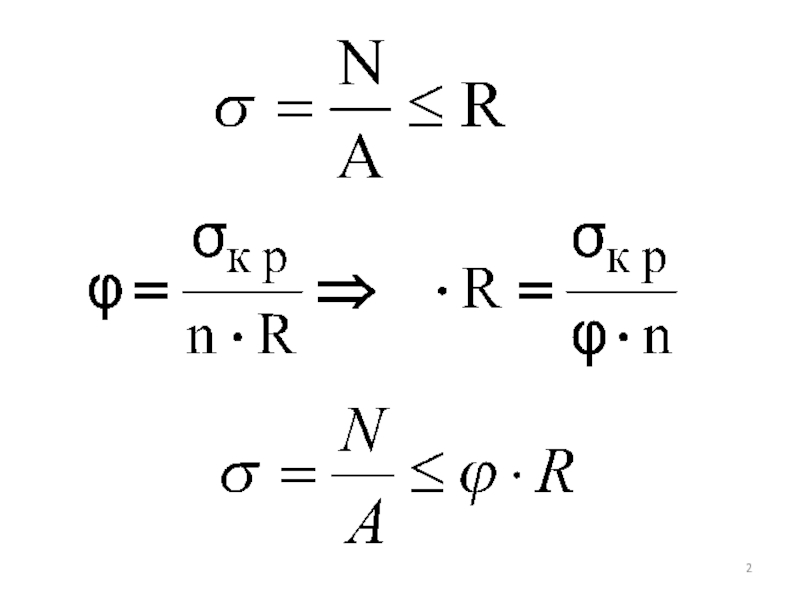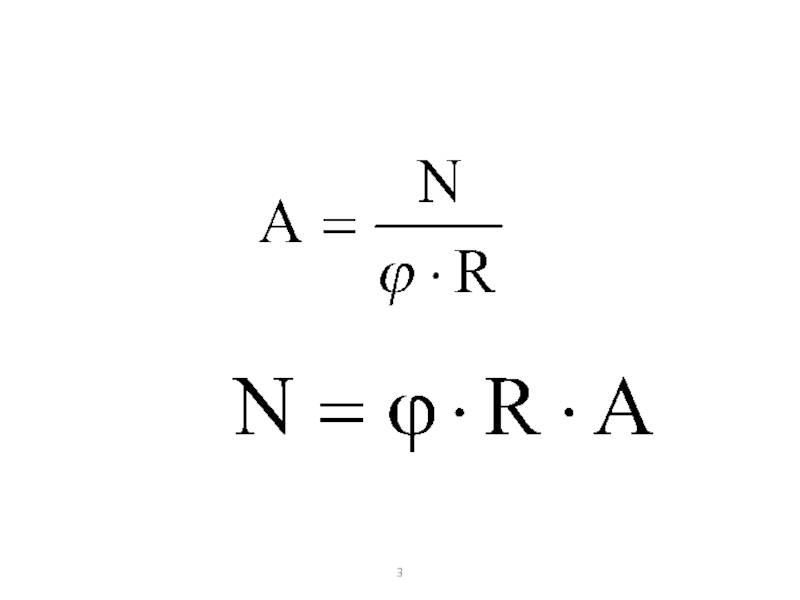Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Практика расчёта сжатых стержней
Содержание
- 1. Практика расчёта сжатых стержней
- 2. Слайд 2
- 3. Слайд 3
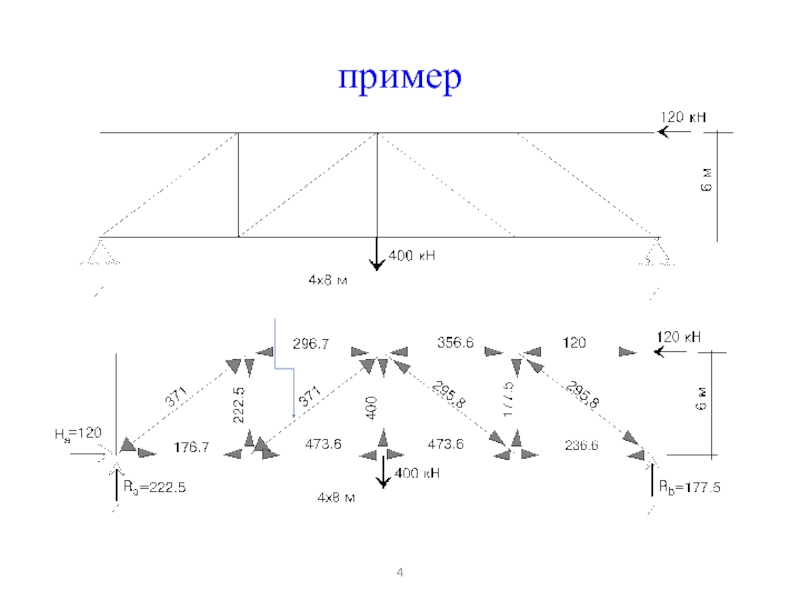
- 4. пример
- 5. Примем сечение из двух неравнобоких уголков . Площадь сечения одного уголка. A1=18.6/2=9.3 см2
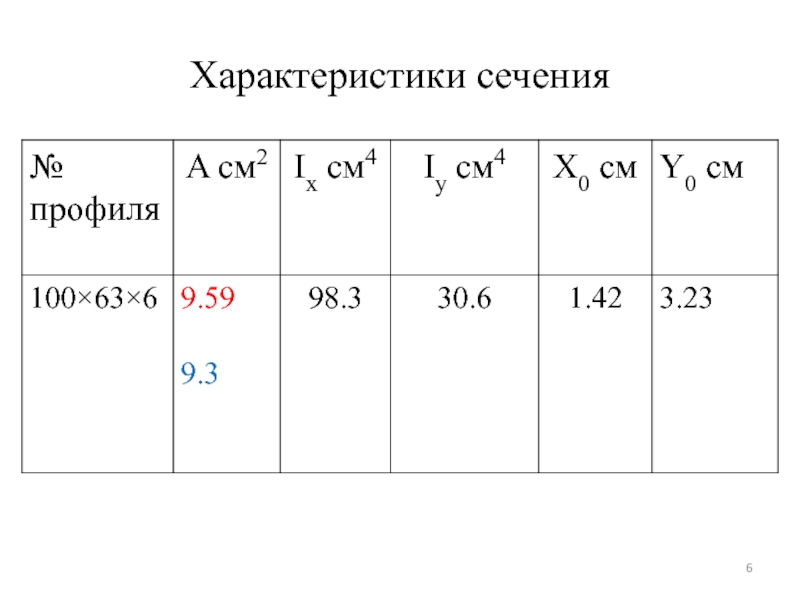
- 6. Характеристики сечения
- 7. 1)Стержень запроектирован из двух уголков таким образом,
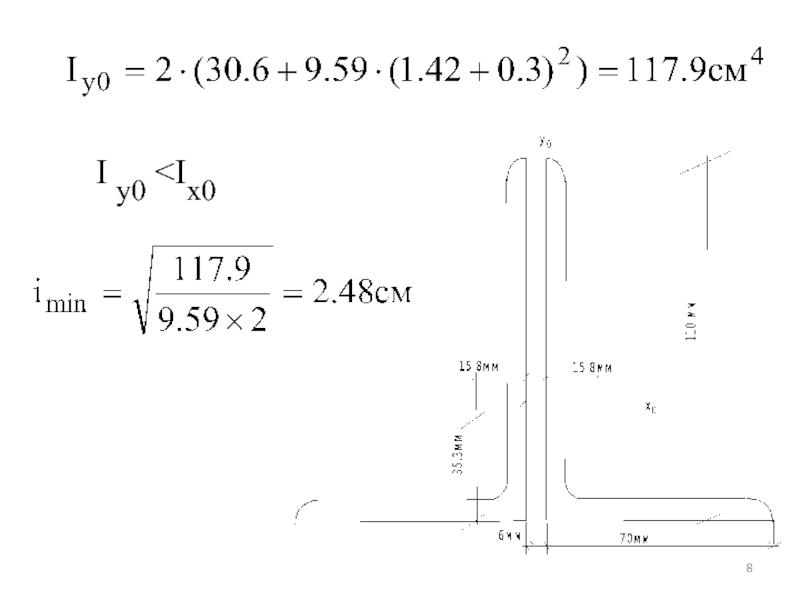
- 8. I y0
- 9. Вычислим гибкость стержня. Для этого нужно учесть
- 10. Из плоскостиВ плоскостиФормула Эйлера
- 11. Таким образом, из условий устойчивости стержень не
- 12. Состыкуем уголки короткими полками. Плоскость больших
- 13. Если потеря устойчивости будет проходить в плоскости фермы, значит =1.ТогдаПри потере устойчивости из плоскости фермы
- 14. Гибкость находится практически на границе применимости формулы
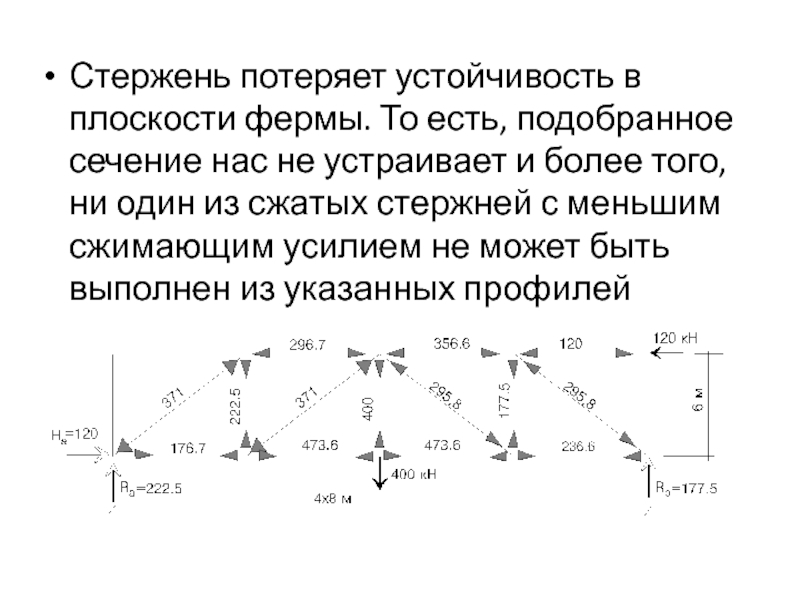
- 15. Стержень потеряет устойчивость в плоскости фермы. То
- 16. 1-ая попытка. Зададимся 0=0.5 № профиля
- 17. аВ таблице коэффициенты устойчивости определены с шагом
- 18. bIy0=2(100+(4.14+0.3)219.7)=976.7 см4Сравнивая результаты (a) и (b), приходим к выводу, что стержень теряет устойчивость в плоскости фермы.
- 19. 2 -ая попытка2-ая попытка:Примем 1=0.5(0+251)=0.5(0.5+0.099)=0.299Ix0=21123=2246см4Iy0=2(324+(5.97+0.3)233.7)=3297.7 см4
- 20. cДля найденного значения гибкости коэффициент будет находиться между 170=0.259 и 180=0.233.
- 21. 33-тья попытка:Примем 2=0.5(1+173.2)=0.5(0.299+0.251)=0.275Ix0=21449=2898см4Iy0=2(446+(6.50+0.3)234.9)=4119 см4
- 22. 3а
- 23. окИз условий прочности Вывод: напряженно-деформированное состояние сжатого
- 24. Крит. силаВеличина критической силы равна
- 25. алгоритм1.Зададимся 0A1Imin если да, то конец, если нет, то на 1.
- 26. Скачать презентанцию
пример
Слайды и текст этой презентации
Слайд 5Примем сечение из двух неравнобоких уголков . Площадь сечения одного
уголка. A1=18.6/2=9.3 см2
Слайд 71)Стержень запроектирован из двух уголков таким образом, что плоскости больших
полок находятся в плоскости фермы. Момент инерции относительно главной центральной
оси, параллельной коротким полкам I x0 =98.32 =196.6 см4, а относительно главной центральной оси y0, проходящей между длинными полками при толщине фасонки 6 ммСлайд 9Вычислим гибкость стержня. Для этого нужно учесть способ закрепления концов
стержня. Минимальную жесткость стержень имеет относительно оси, лежащей в плоскости
фермы (y0). Из плоскости концы стержня можно считать жестко защемленными в узлах (=0.5).,
Формула Эйлера
Слайд 11Таким образом, из условий устойчивости стержень не может быть запроектирован
из уголков выбранных из условий прочности. Кроме того, стержень потеряет
устойчивость в плоскости фермы (58.9<142 Кн), несмотря на то, что минимальную жесткость стержень имеет относительно оси, лежащей в плоскости фермыСлайд 12 Состыкуем уголки короткими полками. Плоскость больших полок нормальна плоскости
фермы.
Главный момент инерции относительно оси, нормальной к плоскости фермы
Ix0 =230.6=61.2
см4,а главный момент инерции, относительно оси, проходящей по нормали к большим полкам, при толщине фасонки 6 мм.
Iy0=2(98.3+(3.28+0.3)29.59)=
=435.6 см4.
Imin= Ix0
Формула Эйлера
Слайд 13Если потеря устойчивости будет проходить в плоскости фермы, значит =1.
Тогда
При
потере устойчивости из плоскости фермы
Слайд 14Гибкость находится практически на границе применимости формулы Эйлера.
Поэтому определим критическую
силу и по Эйлеру и по Ясинскому
к=310.0-1.14104.8=190.5 МПа
Pкр=крA=190.5103КПа19.810-4м2=
=377.2Кн>371Кн
Слайд 15Стержень потеряет устойчивость в плоскости фермы. То есть, подобранное сечение
нас не устраивает и более того, ни один из сжатых
стержней с меньшим сжимающим усилием не может быть выполнен из указанных профилейСлайд 161-ая попытка. Зададимся 0=0.5 № профиля A см2
Ix см4 Iy см4
y0 см x0 см 1258010 19.7 312 100 4.14 1.92 Ix0=2312=624см4Подберём сечение стержня фермы из условий устойчивости
Слайд 17а
В таблице коэффициенты устойчивости определены с шагом 10.Для найденного значения
гибкости коэффициент будет находится между (260)=0.09 и (250)=0.10. Принимают, что
в этом интервале изменяется по линейному закону.Слайд 18b
Iy0=2(100+(4.14+0.3)219.7)=976.7 см4
Сравнивая результаты (a) и (b), приходим к выводу, что
стержень теряет устойчивость в плоскости фермы.
Слайд 192 -ая попытка
2-ая попытка:
Примем 1=0.5(0+251)=0.5(0.5+0.099)=0.299
Ix0=21123=2246см4
Iy0=2(324+(5.97+0.3)233.7)=3297.7 см4
Слайд 20c
Для найденного значения гибкости коэффициент будет находиться между 170=0.259 и
180=0.233.
Слайд 213
3-тья попытка:
Примем 2=0.5(1+173.2)=0.5(0.299+0.251)=0.275
Ix0=21449=2898см4
Iy0=2(446+(6.50+0.3)234.9)=4119 см4
Слайд 23ок
Из условий прочности
Вывод: напряженно-деформированное состояние сжатого стержня удовлетворяет условиям
устойчивости и прочности.
Принимаем стержень из двух уголков №20/12.5 с толщиной
полки 11 мм.Моменты инерции для сечения принятого стержня составляет
Imin=Ix0=2898 см4,
Imax=Iy0=4119 см4