Релятивистская динамика

и тот же вид во всех инерциальных системах отсчета. Этому

принципу должны удовлетворять, в том числе, законы сохранения импульса, энергии и 2-й закон динамики Ньютона. Прежняя форма 2-го закона Ньютона

где

не является релятивистски инвариантной, так как она меняет свой вид при переходе из одной инерциальной системы отсчета в другую.
Для нахождения нового, релятивистски инвариантного уравнения динамики воспользуемся свойством инвариантности интервала между двумя событиями

в инерциальной системе отсчета К. Компонентами этого вектора выступают три

проекции на декартовы оси и одна проекция на ось времени


При переходе к новой инерциальной системе отсчета К´, движущейся относительно К вдоль оси у со скоростью V эти компоненты меняются согласно преобразованиям Лоренца


 Δx´ = Δx Δz´ = Δz



При этом интервал (длина 4-х мерного вектора) не меняется Δs = Δs´

на 4-е оси системы К

где Аt – аналог сΔt

Потребуем, чтобы при переходе к новой системе координат К´ компоненты этого вектора преобразовывались также как и разности координат двух точек





Тогда “длина” вектора будет инвариантом, как и интервал

закон связывает две физические величины А и В, которые в

инерциальной системе К изображаются 4-х мерными векторами в пространстве Минковского



Тогда релятивистски инвариантный закон можно записать в виде равенства этих векторов, поскольку преобразования двух векторов при переходе к новой инерциальной системе отсчета К´ происходят по одинаковым формулам и значит равенство этих векторов, то есть физический закон, не будет менять свою форму


в компонентах

скоростью
относительно неподвижной инерциальной системы К. Пусть за время dt частица

переместилась на вектор .
Составим 4-х мерный вектор с компонентами


Если умножить этот вектор на некоторую постоянную, то получим снова 4-х мерный вектор. Выберем в качестве такой постоянной


где m0 – некоторая константа,

– собственное время, в системе отсчета,
связанной с частицей.

(9.8.1)

(9.8.2)


Если частица движется медленно, так что υ/c <<1, m ≈ m0 , то пространственная составляющая 4-х мерного вектора нерелятивистской частицы будет равна импульсу в ньютоновской механике

если m0 отождествить с массой частицы в нерелятивистской механике. Ее называют массой покоя - это масса частицы в системе, относительно которой частица находится в состоянии покоя.
В релятивистской механике вектор импульса вводится по аналогии согласно
(9.8.3)
m – релятивистская масса

двух шаров показывает, что суммарный импульс системы сохраняется.
Вектор импульса можно

записать в другом виде


(9.8.4)


где dt0 - собственное время.
Эксперименты на ускорителях элементарных частиц подтверждают, что релятивистский импульс, определенный формулами (9.8.3-9.8.4), сохраняется во всех процессах столкновений.
При приближении скорости частицы к скорости света
релятивистская масса частицы m неограниченно растет.

релятивистской динамики материальной точки

(9.8.5)

в общем случае не совпадает с направлением силы.

Значит, сопротивление

тела движущей силе зависит от угла между силой и скоростью.
Поэтому в релятивистской механике масса тела перестает играть роль меры инертности тела.

элементарная работа на малом перемещении равна приращению кинетической энергии

9.9 Взаимосвязь массы и энергии

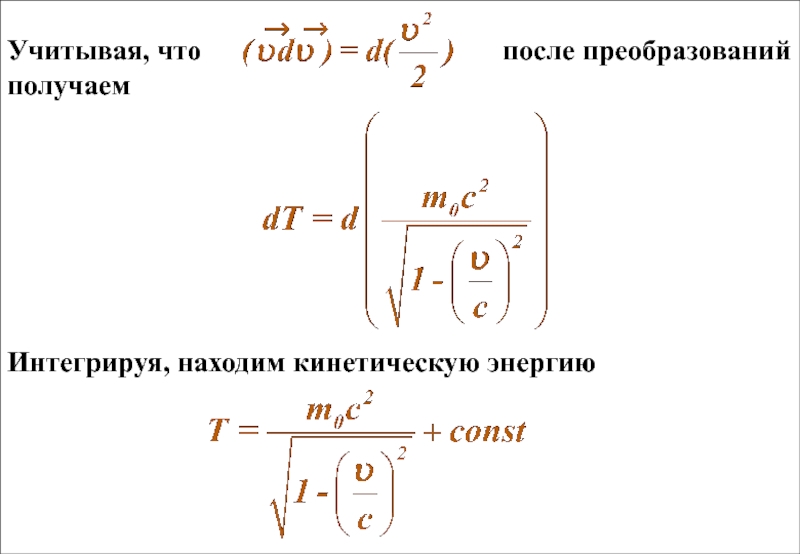
после преобразований получаем







Интегрируя, находим кинетическую энергию

равна нулю.
Полагаем


Поэтому кинетическая энергия релятивистской частицы равна

(9.9.1)



Для малых скоростей получаем нерелятивистское выражение для кинетической энергии

называется энергией покоя.

Энергия покоя является внутренней энергией тела, она не связана с его движением как целого. Если тело состоит из многих частиц, то энергия покоя равна сумме энергий покоя этих частиц, их кинетических энергий движения относительно центра масс и потенциальной энергии взаимодействия друг с другом.
Сумма кинетической энергии и энергии покоя дает
полную энергию свободной частицы

(9.9.2)



Эта формула выражает собой взаимосвязь между массой тела и его энергией. Она показывает, что всякое изменение массы тела приводит к изменению его энергии.

тела во внешнем поле.
Используя выражение для релятивистский импульса, выразим

полную энергию свободной частицы через импульс






Отсюда находим релятивистское соотношение между полной энергией и импульсом частицы



или (9.9.3)

относительно нее со скоростью V вдоль оси y.
Пусть частица

в системе К за малое время dt переместилась на малый вектор с проекциями на декартовые оси dx, dy, dz.
Согласно преобразованиям Лоренца в системе К´частица за время dt´переместится на вектор с проекциями dx´, dy´, dz´
dx´ = dx dz´ = dz

9.10 Законы преобразований релятивистского импульса и энергии

на собственное время частицы dt0 (отсчитанное по часам неподвижным относительно

частицы), а выражение с временами умножим, кроме того, на скорость света с

m0dx´/dt0 = m0dx/dt0

m0dz´/dt0 = m0dz/dt0


(9.10.1)

dx dz´ = dz

то

виде






Аналогично полная энергия частицы в системе K´ равна

двух системах отсчета можно переписать в виде

получим формулу, связывающую полные энергии частицы в этих системах

двух системах

(9.10.2)

величин




образует 4-х мерный вектор - вектор энергии-импульса.
Сравнивая с прежней

формулой (9.8.1) для 4-х мерного вектора


видим, что они совпадают, так как

Из (9.9.3), следует, что “длина” вектора энергии-импульса является инвариантом движения

(9.10.3)