Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стоячие волны
Содержание
- 1. Стоячие волны
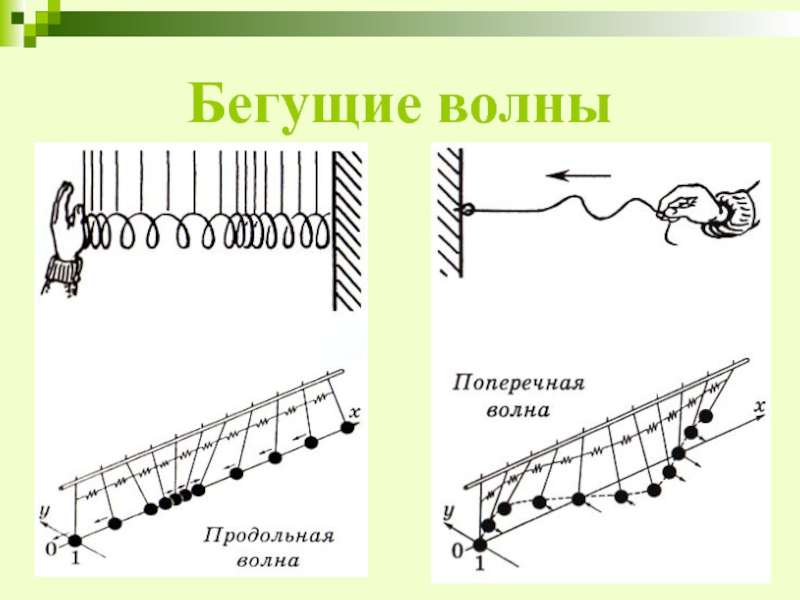
- 2. Бегущие волны
- 3. Образование стоячих волн
- 4. Определение стоячей волны Стоячая волна образуется
- 5. Как движется каждая точка стоячей волны в
- 6. Уравнение стоячей волны
- 7. Узлы и пучности стоячей волныУзлы – неперемещающиеся
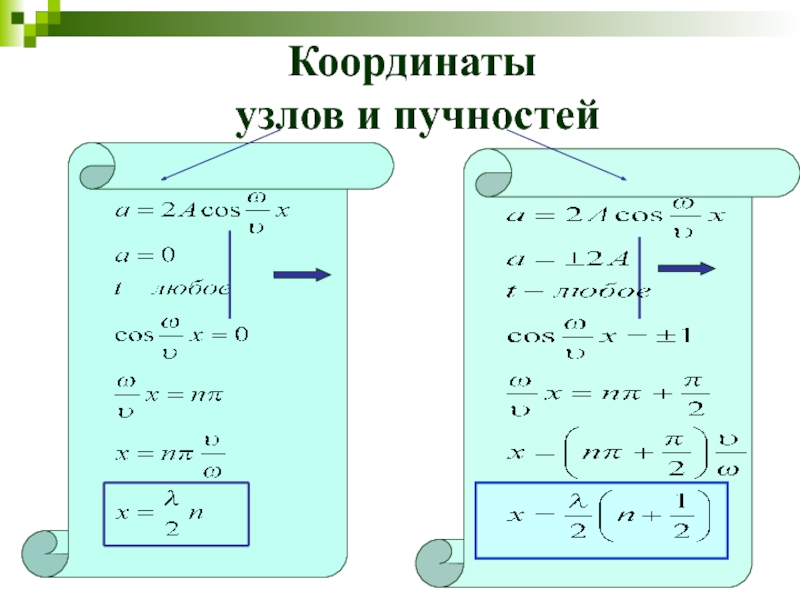
- 8. Координаты узлов и пучностей
- 9. Слайд 9
- 10. Стоячие волны в струнах
- 11. Струнные музыкальные инструменты
- 12. Стоячие волны в воздушных столбах
- 13. Духовые музыкальные инструменты
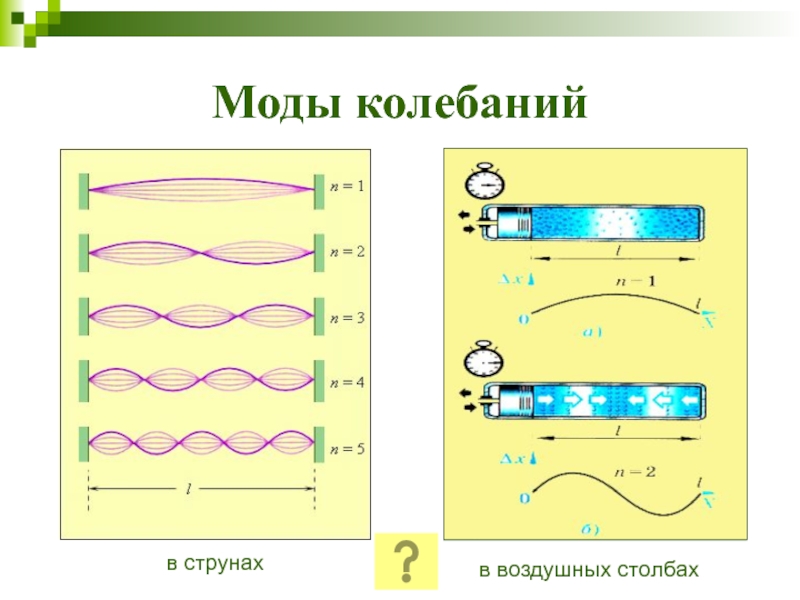
- 14. Моды колебанийв струнахв воздушных столбах
- 15. Частота собственных колебаний струны
- 16. Тембр звука Одной из причин того,
- 17. Ответьте на вопросы:Какая волна называется стоячей?Объясните процесс
- 18. Урок оконченВсем спасибоИспользованные ресурсы:Статья Джо Вулфи «Струны, стоячие волны и гармоники» http://newt.phys.unsw.edu.au/~jw/strings.html.
- 19. Скачать презентанцию
Бегущие волны
Слайды и текст этой презентации
Слайд 1Стоячие волны
Урок физики в 10 классе
(естественно-научный профиль)
© Автор Богданова Ирина
Викторовна
Слайд 3Образование стоячих волн
Посмотрите на
рисунок, который представляет последовательность фаз движения волн во времени (время течет
сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии - при наложении). Отмечены положения (узлы/nodes), в которых обе движущиеся волны нейтрализуют друг друга, и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой.Слайд 4Определение стоячей волны
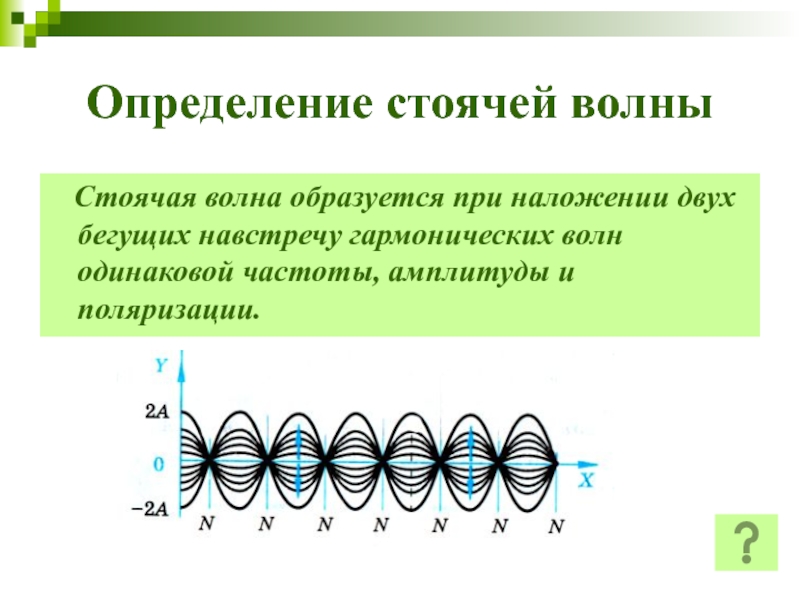
Стоячая волна образуется при наложении двух
бегущих навстречу гармонических волн одинаковой частоты, амплитуды и поляризации.
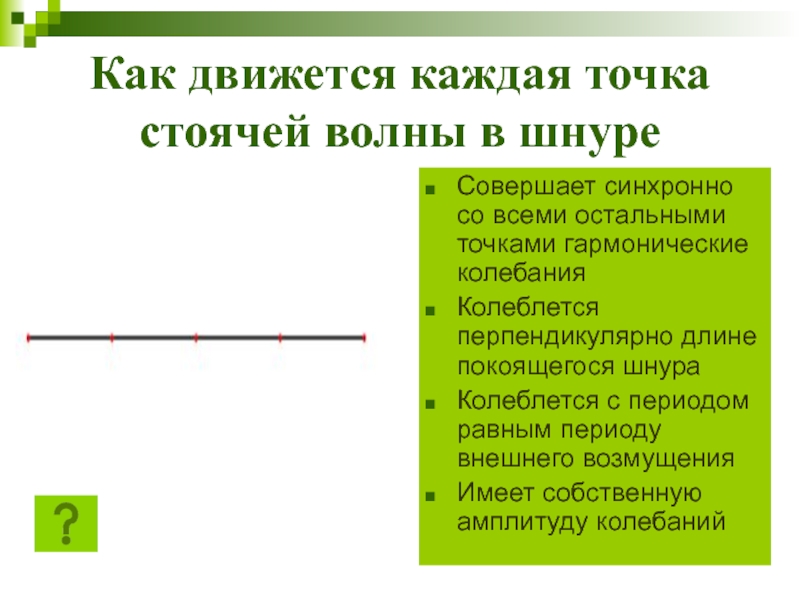
Слайд 5Как движется каждая точка стоячей волны в шнуре
Совершает синхронно со
всеми остальными точками гармонические колебания
Колеблется перпендикулярно длине покоящегося шнура
Колеблется с
периодом равным периоду внешнего возмущенияИмеет собственную амплитуду колебаний
Слайд 7Узлы и пучности стоячей волны
Узлы – неперемещающиеся точки стоячей волны
Пучности
– точки стоячей волны, колеблющиеся с максимальной амплитудой
Слайд 10Стоячие волны в струнах
Если механическая волна, распространяющаяся в среде, встречает на своем пути
какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов.Слайд 12Стоячие волны в воздушных столбах
Трубка Кундта является
простым приспособлением для демонстрации стоячих звуковых волн. Трубка Кундта представляет
собой длинную стеклянную трубку, в которой насыпано немного легкого порошка (например пробковой пыли). Один конец трубки запаян, в другом с помощью пробки укреплен медный стержень. Если потереть стержень наканифоленной замшей, то он начнет скрипеть, а пыль расположится аккуратными кучками вдоль трубки. Такое распределение обусловлено стоячими звуковыми волнами.Слайд 15Частота собственных колебаний струны
На длине
шнура, закрепленного на концах, укладывается целое число полуволн поперечных стоячих
волн.n=1 – основная мода (первая гармоника)
n>1 – n-ая гармоника (n-ый обертон)
У струны имеется целый набор собственных частот, кратных наиболее низкой частоте.
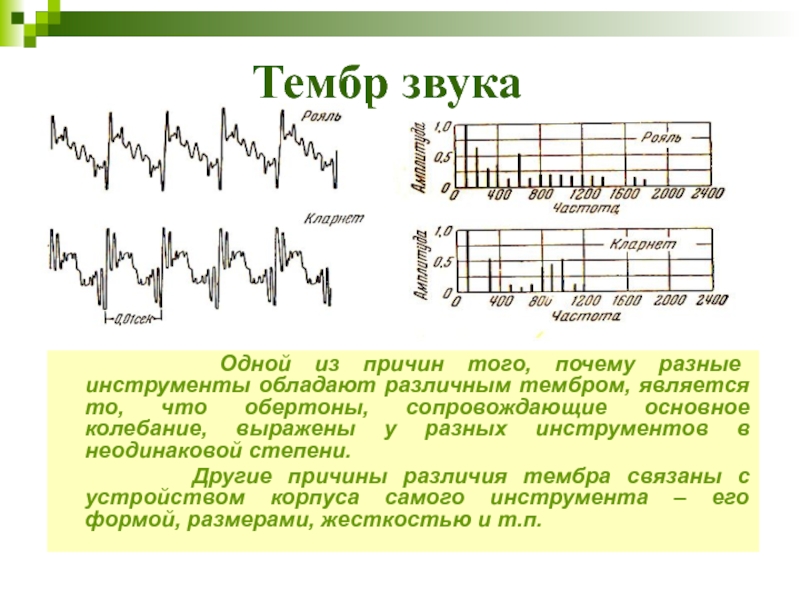
Слайд 16Тембр звука
Одной из причин того, почему разные инструменты
обладают различным тембром, является то, что обертоны, сопровождающие основное колебание,
выражены у разных инструментов в неодинаковой степени.Другие причины различия тембра связаны с устройством корпуса самого инструмента – его формой, размерами, жесткостью и т.п.
Слайд 17Ответьте на вопросы:
Какая волна называется стоячей?
Объясните процесс образования стоячей волны.
Охарактеризуйте
особенности колебаний точки в поперечной стоячей волне.
Сформулируйте определение пучностей и
узлов стоячей волны.При каком условии в струне, закрепленной на концах, образуются стоячие волны?
Что такое первая гармоника собственных колебаний в струне и обертоны?