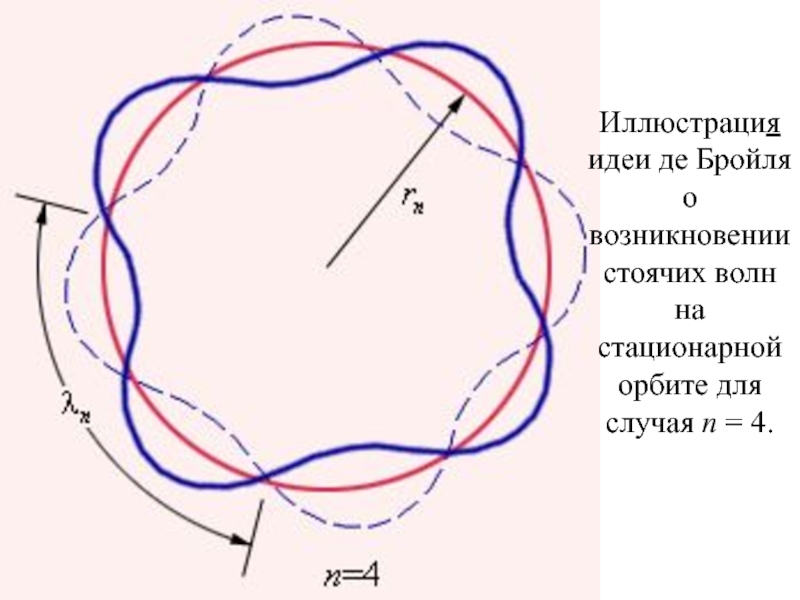
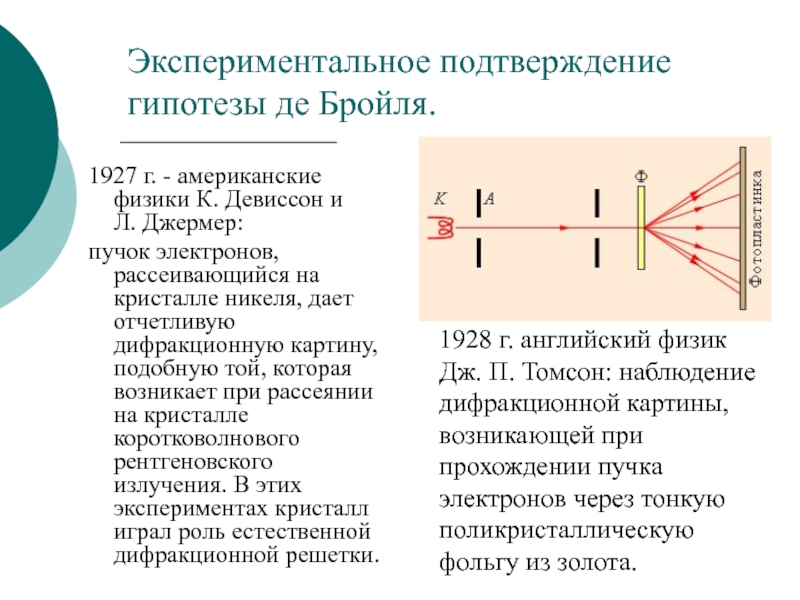
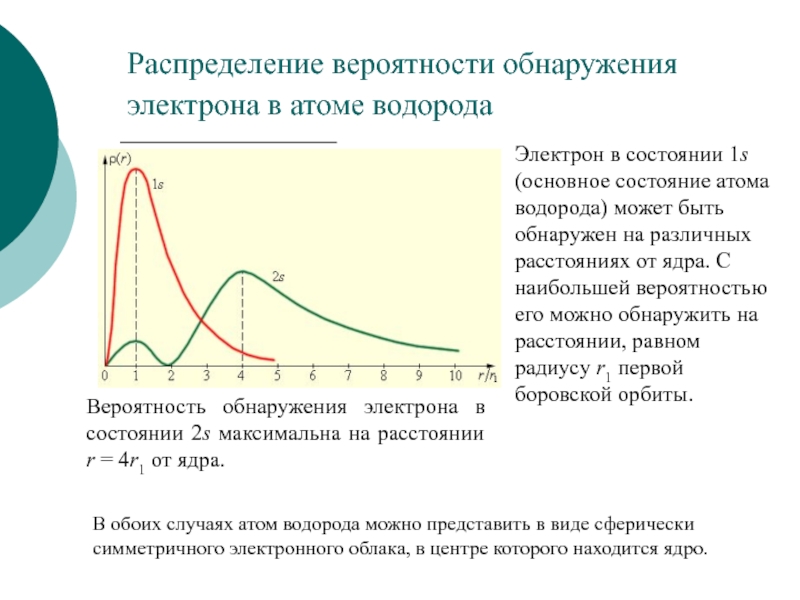
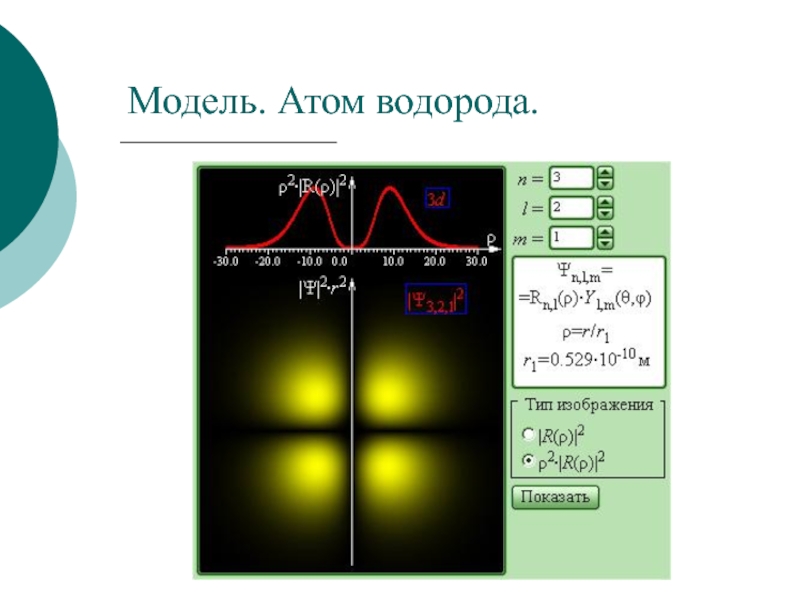
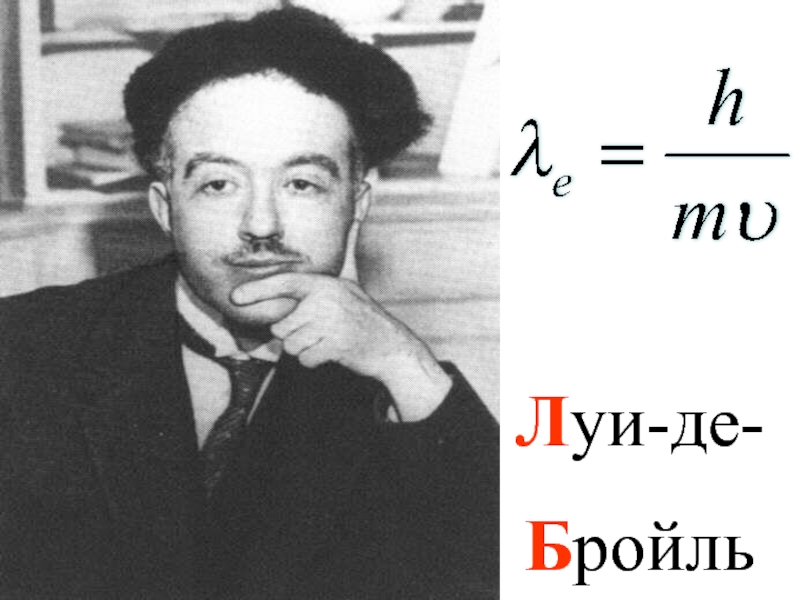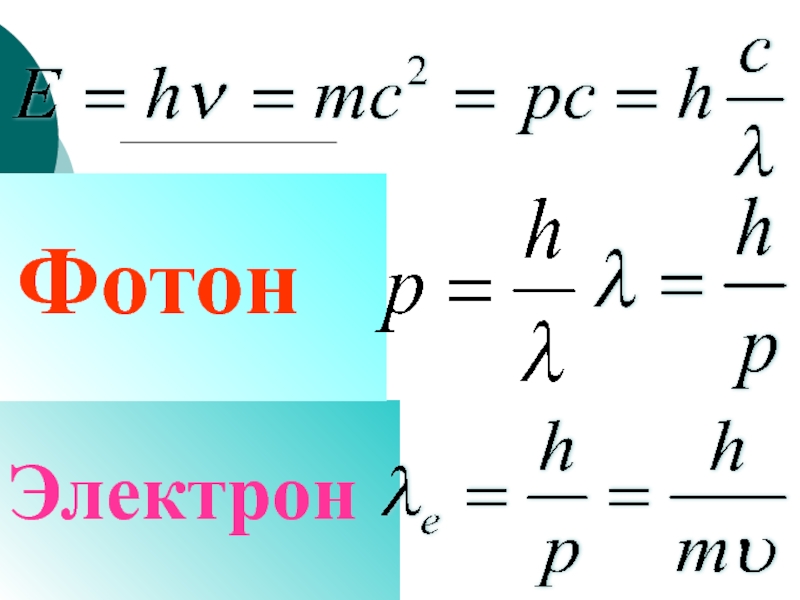электронов в кулоновском поле ядра.
Классическая ядерная модель атома Резерфорда
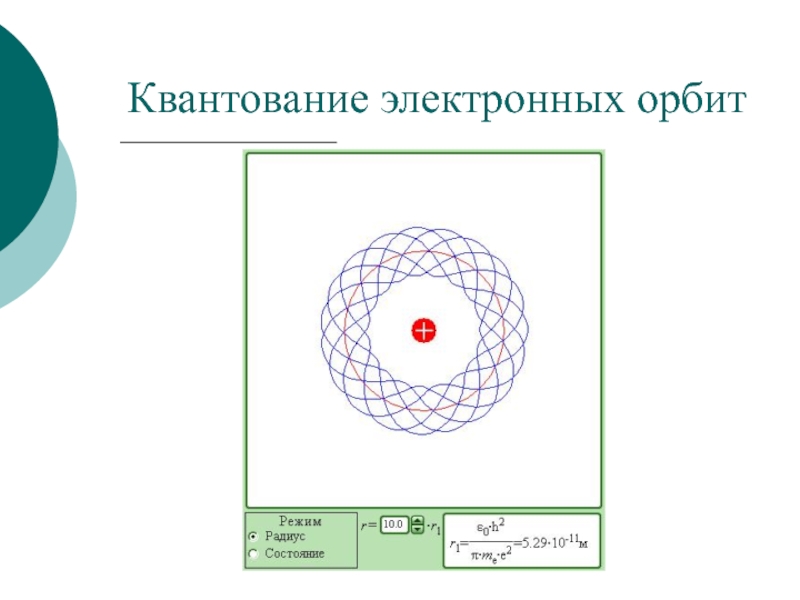
была дополнена в теории Бора идеей о квантовании электронных орбит. Поэтому теорию Бора иногда называют полуклассической.