Взаимодействие дефектов в приближении упругой среды

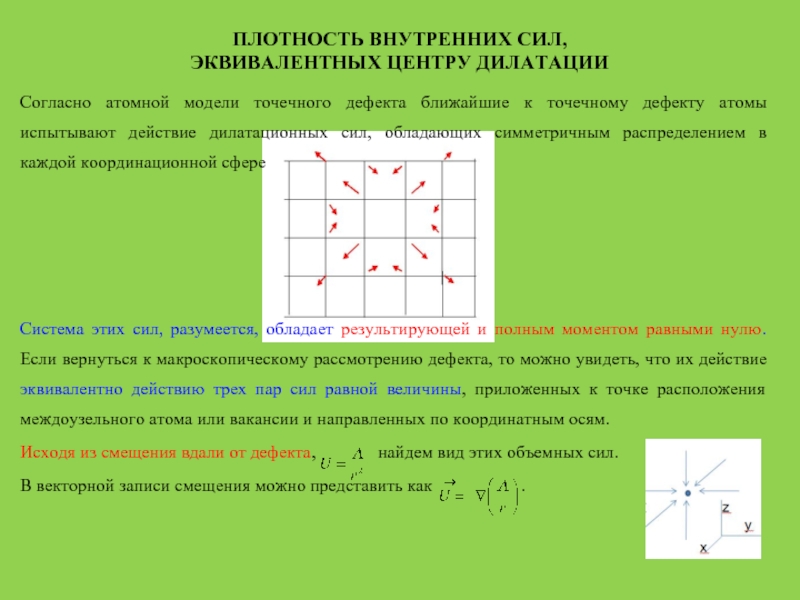
внешнем поле воспользуемся уравнением статического равновесия упругой среды

, здесь fi – плотность объемных сил, действующих внутри образца.
Умножим обе части этого уравнения скалярно на радиус-вектор и проинтегрируем по всему пространству:

Преобразуем левую часть уравнения следующим образом:

при преобразовании было учтено, что . Первый интеграл определяется граничными условиями на поверхности. Во втором интеграле учтем, что , где K – модуль объемного сжатия. Следовательно:

Таким образом, относительное изменение объема кристалла, связанное с действием внутренних сил f и сил на поверхности равно:

ближайшие к точечному дефекту атомы испытывают действие дилатационных сил, обладающих

симметричным распределением в каждой координационной сфере




Система этих сил, разумеется, обладает результирующей и полным моментом равными нулю. Если вернуться к макроскопическому рассмотрению дефекта, то можно увидеть, что их действие эквивалентно действию трех пар сил равной величины, приложенных к точке расположения междоузельного атома или вакансии и направленных по координатным осям.
Исходя из смещения вдали от дефекта, найдем вид этих объемных сил.
В векторной записи смещения можно представить как .

,



где введено обозначение: .


Таким образом, в теории упругости дефект можно описать δ-функционной плотностью сил. Мощность дефекта характеризуется величиной Ω0.
Реакция среды на дефект определяется ее модулем сжатия К.
1. Изменение объема для тела с указанным распределением плотности сил составит величину (слайд 1)

равна нулю везде, за исключением начала координат, то есть, как это получалось и раньше, точечный дефект создает только сдвиговую деформацию в окружающей бесконечной среде.
Естественно, последний вывод справедлив только лишь тогда, когда среда является упруго изотропной, а точечный дефект эквивалентен центру дилатации.
Иначе, упругое поле точечного дефекта, строго говоря, не является чисто сдвиговым.
Обобщение - в общем случае неизотропной среды, возмущение можно записать:



Как правило, характерный объем дефектов для вакансий отрицателен, для междоузлий положителен.
Для простых металлов его величина составляет порядка 0.1ω0 однако, например, для анизотропного графита она достигает больших значений – порядка 5ω0 .
В заключении отметим, что введенный здесь способ описания точечных дефектов – через плотность объемных сил подходит и для описания других типов дефектов, например, дислокаций.

на кристалл, в котором он находится, тремя способами.

Прежде всего,

он вызывает смещение атомов матрицы.

Кроме того, дефект выступает в роли локальной неоднородности, то есть он с одной стороны вносит изменение в массу элементарной ячейки, с другой – дает локальное изменение силовых констант, входящих в закон Гука

внешней нагрузки.
Рассмотрим некоторую общую задачу: дефект в упругом поле

смещения, созданном внешней нагрузкой на среду.

Работа, которую совершает внешнее поле над дефектом при малых смещениях последнего, найдем из работы внешних сил над образцом, содержащим дефект. Последняя равна:

Используем теперь явный вид для объемных сил, соответствующих наличию

точечного дефекта в кристалле , а для преобразования последнего слагаемого в нашем выражении используем закон Гука

Выполним интегрирование по частям в первом слагаемом, во втором – проведем тривиальное интегрирование, а в третьем учтем симметрию:

T=const, δR=δF

дефект, находящийся в точке

Сдвинем дефект на величину




– сила,

с которой упруго деформированный кристалл действует на дефект.

Как видно, точечный дефект взаимодействует с упругим полем двояким образом.
С одной стороны дефект выступает как источник дилатации, это отражено в первом слагаемом линейном по деформациям.
С другой стороны дефект проявляет себя как локальная неоднородность упругих свойств, что передает второе (квадратичное по деформациям) слагаемое.
Первое слагаемое называют размерным эффектом, а второе – модульным эффектом.

и в выражении для энергии и силы оставляют линейное по

упругим деформациям слагаемое:

- простая изотропная среда

Энергия и сила, действующую на центр дилатации, выражается только через среднее гидростатическое давление!!!

Направление силы зависит от типа дефекта.
Для дефекта с отрицательным дилатационным объемом (вакансии) сила направлена в сторону увеличения давления, то есть эти дефекты смещаются в более сжатые области кристалла.
Сила, действующая на дефекты с положительным дилатационным объемом (междоузельные атомы), направлена в сторону понижения давления – дефекты смещаются в разреженные области кристалла.
Чисто сдвиговые деформации никак не взаимодействуют с дефектом

Один дефект создает в матрице поле смещения, а другой дефект,

воспринимая это смещение, должен взаимодействовать с первым. Именно таким образом в рамках теории упругости удается описать взаимодействие дефектов. Взаимодействия такого рода принято называть деформационными.
Однако, точечный дефект в изотропном приближении создает только сдвиговые напряжения, следовательно, и взаимодействие дефектов отсутствует.
Таким образом, два точечных дефекта в изотропной бесконечной среде в линейном приближении не взаимодействуют.
В анизотропных средах мощность точечных дефектов может быть достаточно велика, а упругие поля, создаваемые дефектами не являются чисто сдвиговыми. В таких веществах между дефектами возникает взаимодействие.
Природу деформационного взаимодействия удобно объяснить на приведённой ниже простой аналогии.

от друга размещены небольшие шары (упругая поверхность имитирует плоскую кристаллическую

решётку, а шары - дефекты в ней). Очевидно, что если расстояния между шарами велики, то они не будут "чувствовать" друг друга и расположатся каждый в своей лунке на поверхности. Однако стоит двум шарам сблизиться на некоторое минимальное расстояние, определяемое упругими свойствами поверхности и весом шаров, как под действием упругих сил они начнут двигаться на встречу друг другу и в результате "свалятся" в общую лунку. Очевидно, что при соответствующем начальном расположении в лунке может оказаться и большее количество шаров.
На этом простом примере видно, что деформационное взаимодействие обуславливает взаимное притяжение одноимённых дефектов и может являться реальной причиной образования скоплений дефектов.

обладающем сильными анизотропными свойствами, взаимодействие двух междоузельных атомов, расположенных между

одной и той же парой базисных плоскостей графита, на расстояниях меньших величины r0 ≈ 10 Å, носит характер притяжения. Причем энергия взаимодействия, величина которой достигает значения порядка 1 эВ, сопоставима с энергией ковалентной связи в базисных плоскостях (4.96 эВ). Подчеркнем, что благодаря анизотропии структуры графита область взаимодействия дефектов значительно превосходит межатомные расстояния – объем зоны, в пределах которой два междоузлия притягиваются друг к другу равен Va≈40ω0 . Деформационный потенциал взаимодействия междоузлий, расположенных между соседними парами базисных плоскостей графита, соответствует отталкиванию дефектов. Величина энергии отталкивания на малых расстояниях достигает значения равного 2 эВ.

обладающем сильными анизотропными свойствами.