Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Закон сохранения момента импульса
Содержание
- 1. Закон сохранения момента импульса
- 2. Момент импульса частицы относительно неподвижной точкиПусть частица
- 3. Момент импульса частицы относительно неподвижной осиМоментом импульса
- 4. Момент силыПусть к частице A приложена сила
- 5. Момент силы относительно неподвижной осиМоментом силы Mz
- 6. Уравнение моментовНайдем производную по времени момента импульса L:Производная:Тогда
- 7. Уравнение моментовТаким образом, получаем уравнение моментов:Это уравнение
- 8. ГЛАВА 6 ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА6.2
- 9. Момент импульса частицы при движении в гравитационном
- 10. Основное свойство центрального гравитационного поляТаким образом, доказано
- 11. Следствие 11. Траектория движения частицы в центральном
- 12. Следствие 2 (2-й закон Кеплера)2. (Второй закон
- 13. Следствие 2 (2-й закон Кеплера) Момент импульса частицы: Величина
- 14. ГЛАВА 6 ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА6.3 Закон сохранения момента импульса системы частиц
- 15. Момент импульса системы частицРассмотрим систему частиц, импульсы
- 16. Момент импульса системы, состоящий из 2-х частиц
- 17. Вывод уравнения моментов для системы частицЧтобы найти
- 18. Вывод уравнения моментов для системы частицРассмотрим любые
- 19. Вывод уравнения моментов для системы частицТаким образом,
- 20. Закон сохранения импульса системы частицИз уравнения моментов
- 21. Частные случаи закона сохранения момента импульса незамкнутой
- 22. Частные случаи закона сохранения момента импульса незамкнутой
- 23. Частные случаи закона сохранения момента импульса незамкнутой
- 24. Частные случаи закона сохранения момента импульса незамкнутой
- 25. Частные случаи закона сохранения момента импульса незамкнутой
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГЛАВА 6
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
6.1 Момент импульса частицы. Момент
силы. Уравнение моментов
Слайд 2Момент импульса частицы относительно неподвижной точки
Пусть частица A движется со
скоростью v. Положение частицы в пространстве зададим радиусом-вектором r, проведенным
из неподвижной точки O.Моментом импульса частицы относительно неподвижной точки O называется вектор L:
(где p = mv – импульс частицы).
Угол α – угол между векторами p и r; lp – кратчайшее расстояние от точки O до линии, вдоль которой направлен вектор p (плечо импульса).
Вектор L перпендикулярен плоскости, в которой расположены векторы p и r.
Слайд 3Момент импульса частицы относительно неподвижной оси
Моментом импульса Lz частицы относительно
неподвижной оси Z называется проекция на эту ось момента импульса
L частицы, вычисленная относительно неподвижной точки оси Z.Момент импульса Lz относительно неподвижной оси является скалярной величиной
Значение Lz не зависит от выбора точки O на оси Z.
Слайд 4Момент силы
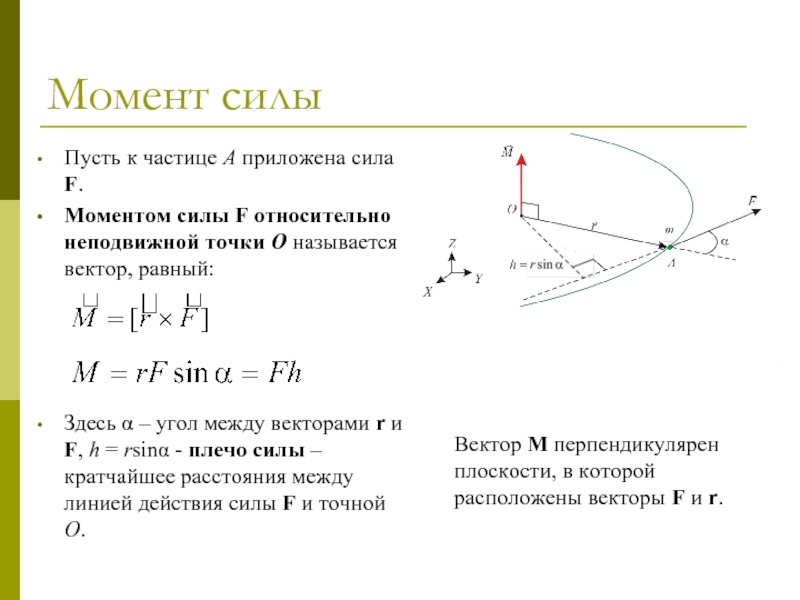
Пусть к частице A приложена сила F.
Моментом силы F
относительно неподвижной точки O называется вектор, равный:
Здесь α – угол
между векторами r и F, h = rsinα - плечо силы – кратчайшее расстояния между линией действия силы F и точной O.Вектор M перпендикулярен плоскости, в которой расположены векторы F и r.
Слайд 5Момент силы относительно неподвижной оси
Моментом силы Mz относительно неподвижной оси
Z называется проекция на эту ось вектора момента силы относительно
произвольной точки O на оси Z.Величина Mz является скалярной и не зависит от выбора точки O на оси Z.
Слайд 7Уравнение моментов
Таким образом, получаем уравнение моментов:
Это уравнение показывает, что производная
по времени момента импульса частицы равна моменту действующей на нее
силы.
Слайд 8ГЛАВА 6
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
6.2 Момент импульса частицы при
движении в гравитационном поле. Второй закон Кеплера
Слайд 9Момент импульса частицы при движении в гравитационном поле
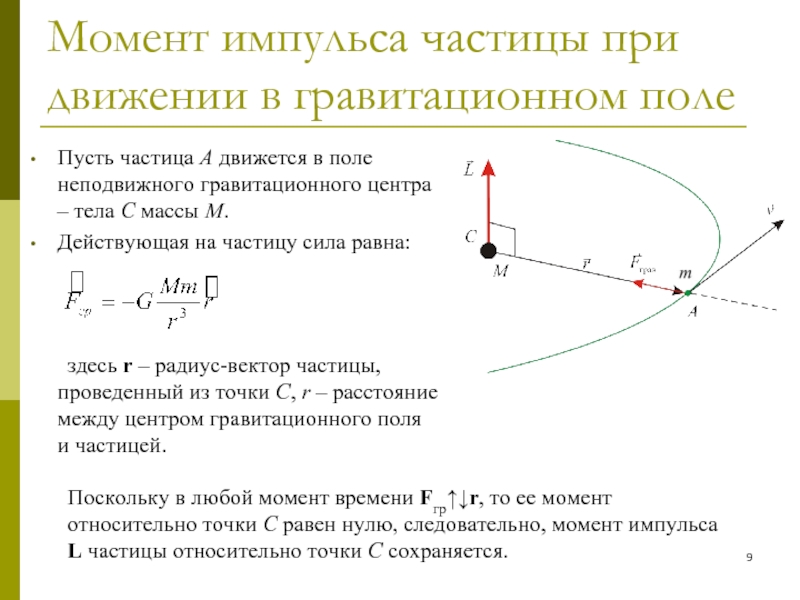
Пусть частица A
движется в поле неподвижного гравитационного центра – тела C массы
M.Действующая на частицу сила равна:
здесь r – радиус-вектор частицы, проведенный из точки C, r – расстояние между центром гравитационного поля и частицей.
Поскольку в любой момент времени Fгр↑↓r, то ее момент относительно точки C равен нулю, следовательно, момент импульса L частицы относительно точки C сохраняется.
Слайд 10Основное свойство центрального гравитационного поля
Таким образом, доказано основное свойство центрального
гравитационного поля: при движении в центральном гравитационном поле момент импульса
частицы относительно центра поля сохраняетсяРассмотрим следствия, вытекающие из этого свойства.
Слайд 11Следствие 1
1. Траектория движения частицы в центральном гравитационном поле является
плоской кривой; плоскость движения проходит через центр поля.
При движении частицы
ее момент импульса относительно поля L = [r×p]. По свойству векторного произведения, r⊥L. А поскольку вектор L = const, его направление в пространстве остается неизменным. Следовательно, при движении частицы вектор r остается в одной плоскости, перпендикулярной к L, которая проходит через центр поля. Что и требовалось доказать.Слайд 12Следствие 2 (2-й закон Кеплера)
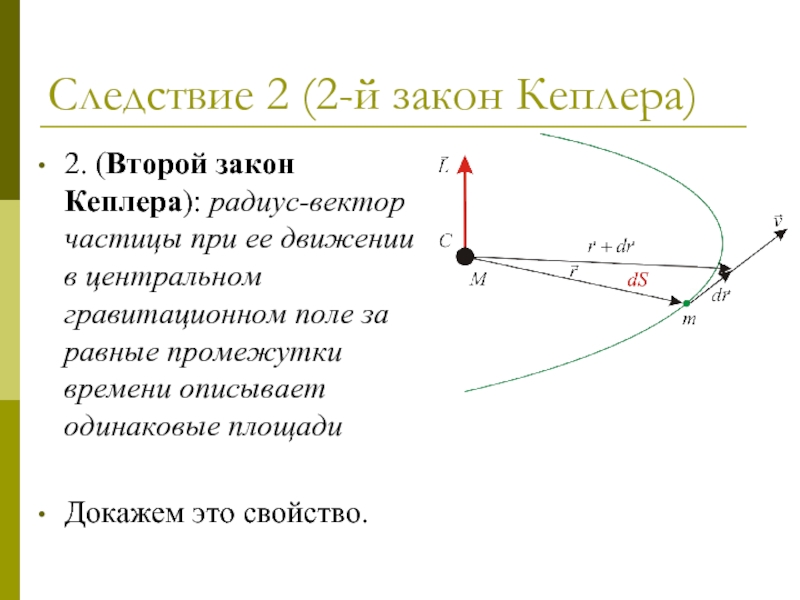
2. (Второй закон Кеплера): радиус-вектор частицы
при ее движении в центральном гравитационном поле за равные промежутки
времени описывает одинаковые площадиДокажем это свойство.
Слайд 13Следствие 2 (2-й закон Кеплера)
Момент импульса частицы:
Величина σ = dS/dt
называется секториальной скоростью (площадь, описываемая за единицу времени радиусом-вектором частицы).
Поскольку
L = const, то и σ = const.Слайд 14ГЛАВА 6
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
6.3 Закон сохранения момента импульса
системы частиц
Слайд 15Момент импульса системы частиц
Рассмотрим систему частиц, импульсы которых в некоторой
системе отсчета равны p1, p2, …, pi, …, pN. Положения
этих частиц в пространстве задаются радиусами-векторами r1, r2, …, ri, …, rN, проведенными из некоторой неподвижной точки O (неподвижного начала).Моментом импульса L системы частиц относительно неподвижной точки O называется векторная сумма всех моментов импульса Li всех частиц системы относительно той же точки:
Слайд 16Момент импульса системы, состоящий из 2-х частиц
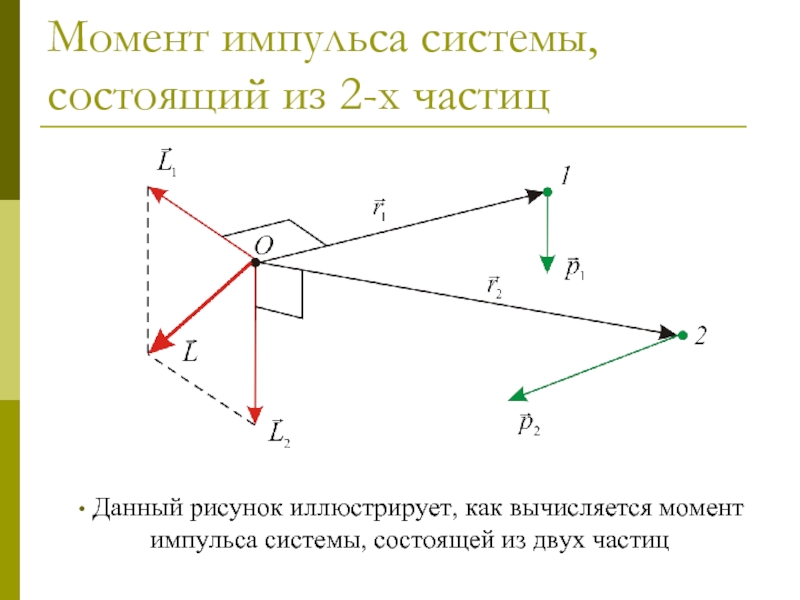
Данный рисунок иллюстрирует,
как вычисляется момент импульса системы, состоящей из двух частиц
Слайд 17Вывод уравнения моментов для системы частиц
Чтобы найти физическую величину, которая
определяет скорость изменения момента импульса системы частиц, продифференцируем по времени
обе части формулы для L:(поскольку на каждую частицу действуют как внутренние, так и внешние силы).
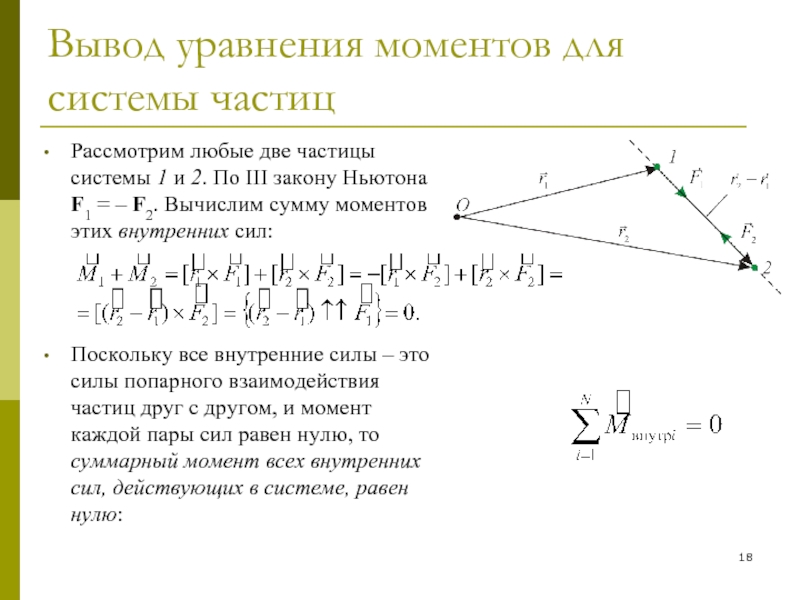
Слайд 18Вывод уравнения моментов для системы частиц
Рассмотрим любые две частицы системы
1 и 2. По III закону Ньютона F1 = –
F2. Вычислим сумму моментов этих внутренних сил:Поскольку все внутренние силы – это силы попарного взаимодействия частиц друг с другом, и момент каждой пары сил равен нулю, то суммарный момент всех внутренних сил, действующих в системе, равен нулю:
Слайд 19Вывод уравнения моментов для системы частиц
Таким образом, получаем уравнение моментов
для системы частиц:
В соответствии с этим уравнением, производная по времени
момента импульса системы частиц равна сумме моментов всех внешних сил, действующих на частицы.
Слайд 20Закон сохранения импульса системы частиц
Из уравнения моментов вытекает закон сохранения
импульса системы частиц: момент импульса L замкнутой системы частиц с
течением времени не изменяется (т.е. сохраняется).Действительно, если система замкнута, т.е. внешние силы отсутствуют, то:
Однако, в некоторых случаях момент импульса незамкнутой системы частиц может сохраняться. Рассмотрим эти случаи.
Слайд 21Частные случаи закона сохранения момента импульса незамкнутой системы частиц
1. Если
система не замкнута, но моменты внешних сил, вообще говоря, отличны
от нуля, но при этом сумма моментов внешних сила равна нулю, то момент импульса системы сохраняется:
Слайд 22Частные случаи закона сохранения момента импульса незамкнутой системы частиц
Пример. Летевшая
горизонтально пуля со скоростью v0 массой m застревает в небольшом
деревянном шаре массой M, подвешенном на вертикальном стержне, который может свободно вращаться вокруг горизонтальной оси, проходящей через точку подвеса O.На пулю и шар действуют внешние силы mg, Mg и N (сила N в момент удара пули может быть очень большой). Однако, если за время удара стержень не успевает значительно отклониться, то моменты всех внешних сил относительно точки O равны нулю (линии действия этих сил проходят через точку O), то момент импульса системы сохраняется:
Слайд 23Частные случаи закона сохранения момента импульса незамкнутой системы частиц
2. Если
проекция на некоторую неподвижную ось Z момента всех внешних сил
равна нулю, то в проекции на ось Z момент импульса Lz сохраняется:
Слайд 24Частные случаи закона сохранения момента импульса незамкнутой системы частиц
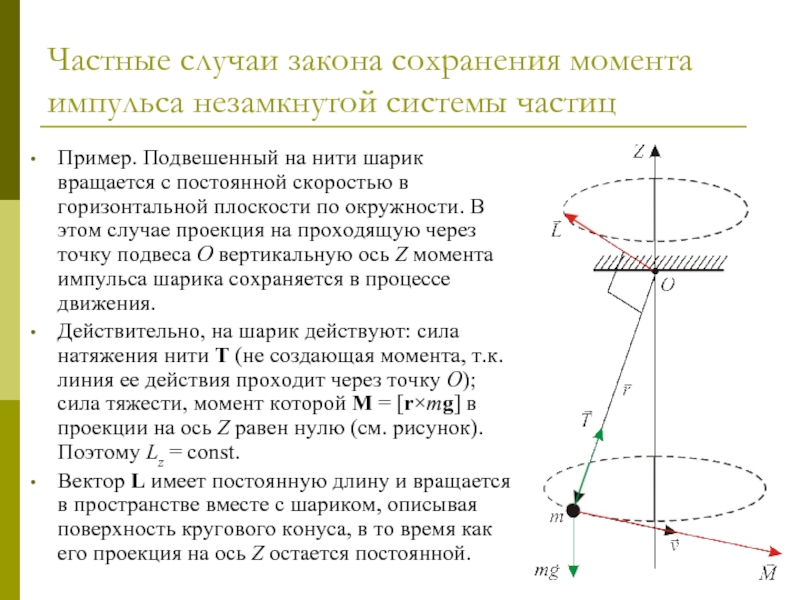
Пример. Подвешенный
на нити шарик вращается с постоянной скоростью в горизонтальной плоскости
по окружности. В этом случае проекция на проходящую через точку подвеса O вертикальную ось Z момента импульса шарика сохраняется в процессе движения.Действительно, на шарик действуют: сила натяжения нити T (не создающая момента, т.к. линия ее действия проходит через точку O); сила тяжести, момент которой M = [r×mg] в проекции на ось Z равен нулю (см. рисунок). Поэтому Lz = const.
Вектор L имеет постоянную длину и вращается в пространстве вместе с шариком, описывая поверхность кругового конуса, в то время как его проекция на ось Z остается постоянной.
Слайд 25Частные случаи закона сохранения момента импульса незамкнутой системы частиц
3. Момент
импульса системы приблизительно сохраняется, если момент Mвнеш ограниченной по модулю
внешней силы действует в течение короткого промежутка времени Δt (т.е. Δt ≈ 0):