Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитическое задание кривых на плоскости
Содержание
- 1. Аналитическое задание кривых на плоскости
- 2. Введение. При написании реферата я поставила перед
- 3. Введение.Металлическая пластинка с профилем в виде половины
- 4. Введение. Разнообразные задачи из физики и математики,
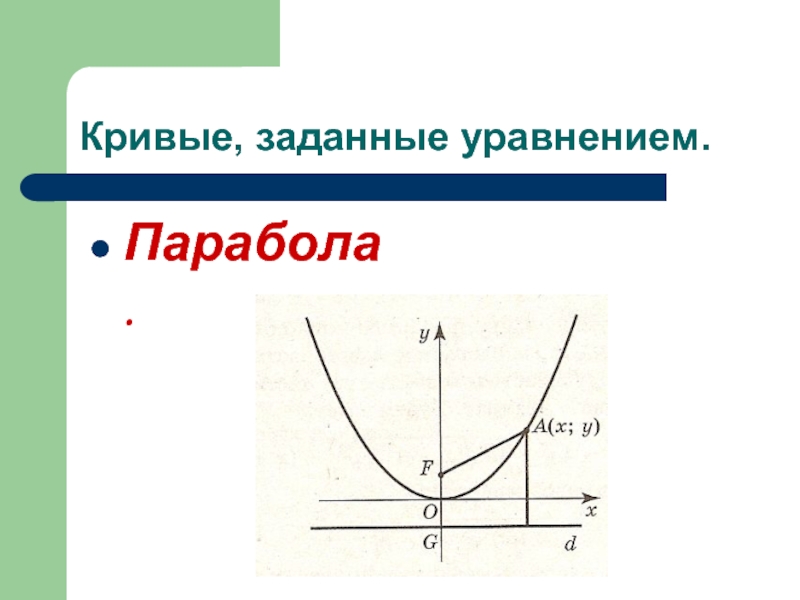
- 5. Кривые, заданные уравнением.Парабола.
- 6. Уравнение параболы.
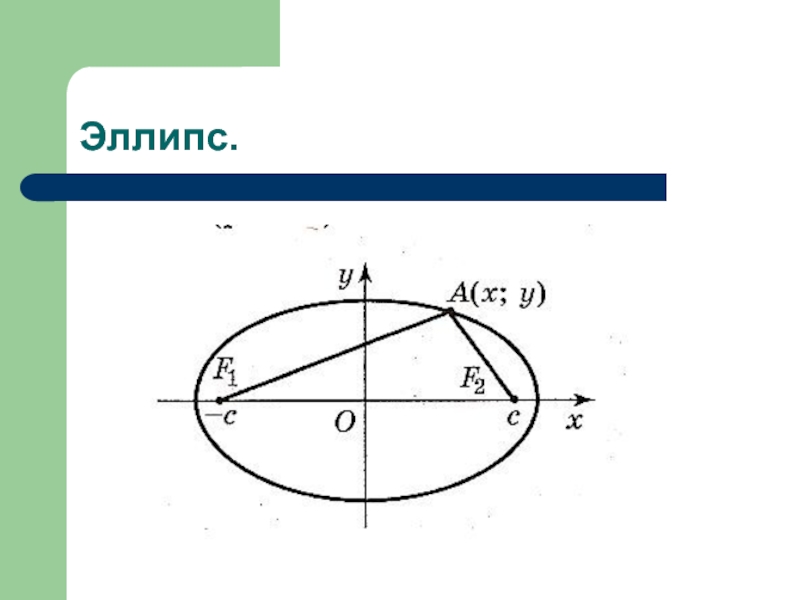
- 7. Эллипс.
- 8. Уравнение эллипса.
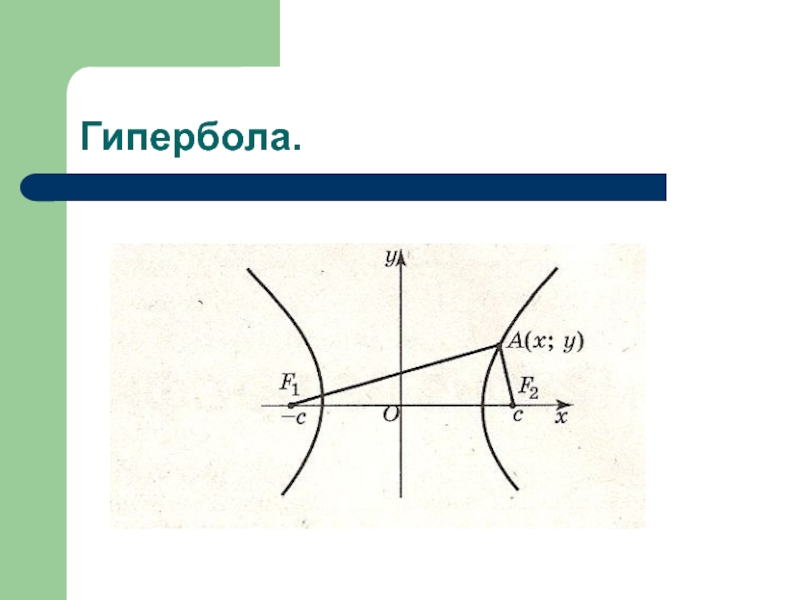
- 9. Гипербола.
- 10. Уравнение гиперболы.
- 11. Лист Декарта.
- 12. Уравнение листа Декарта.
- 13. Кривые, заданные уравнениями в полярных координатах.
- 14. Полярные координаты. Полярными координатами точки А на
- 15. Связь между полярными и декартовыми координатами.
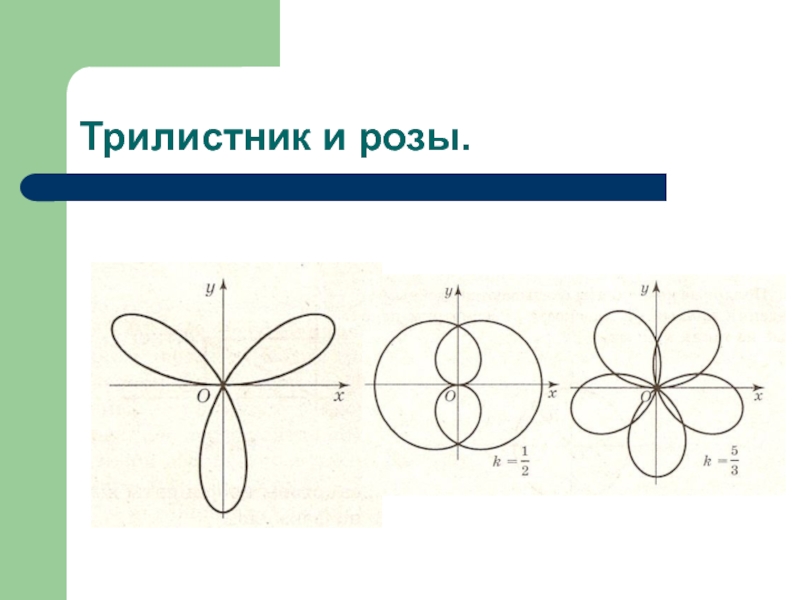
- 16. Трилистник и розы.
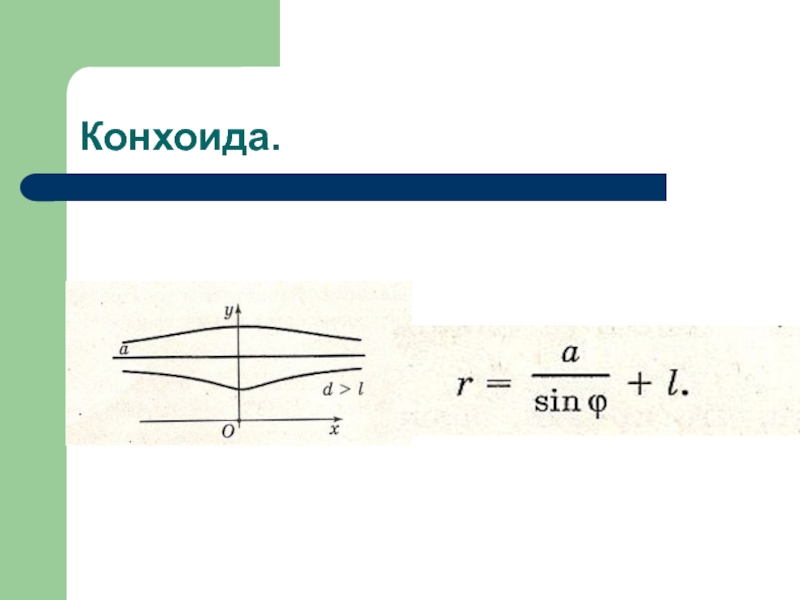
- 17. Конхоида.
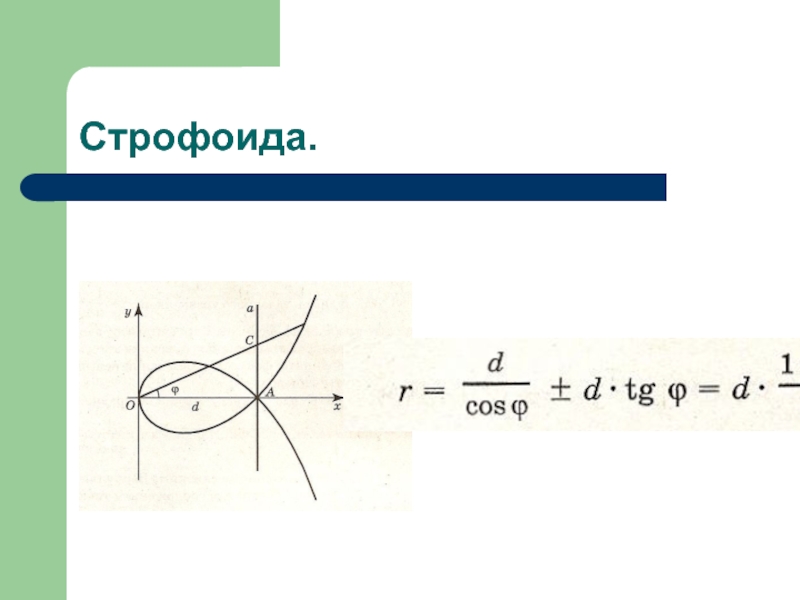
- 18. Строфоида.
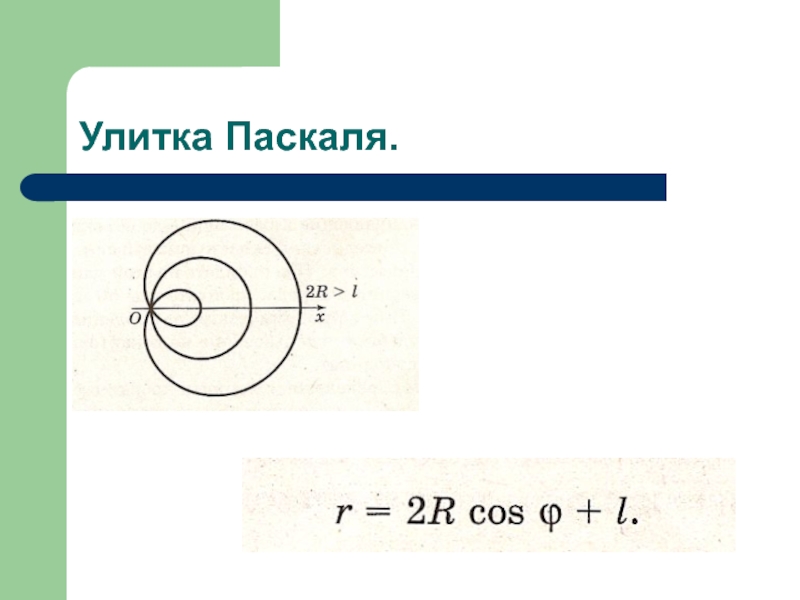
- 19. Улитка Паскаля.
- 20. Лист щавеля.
- 21. Спирали.
- 22. Спираль Архимеда. Геометрическим свойством, характеризующим спираль Архимеда,
- 23. Логарифмическая спираль.
- 24. Кривые, заданные параметрическими уравнениями.
- 25. Параметрическое уравнение окружности.
- 26. Параметрическое уравнение листа Декарта.
- 27. Циклоида.Рассмотрим циклоиду – кривую, которая описывается точкой,
- 28. Параметрическое уравнение циклоиды.
- 29. Виды циклоиды: Если d < R, то кривая называется укороченной циклоидой.
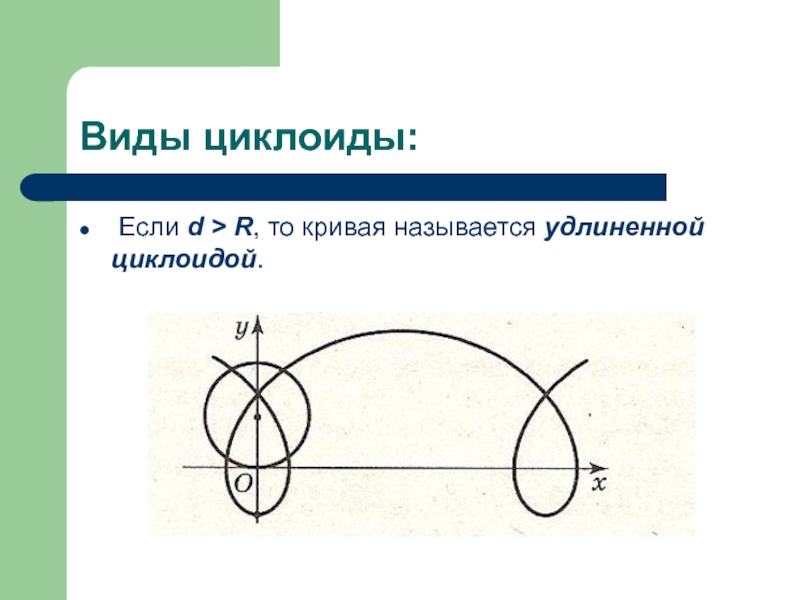
- 30. Виды циклоиды: Если d > R, то кривая называется удлиненной циклоидой.
- 31. Кардиоида. Кардиоида – кривая, являющаяся траекторией движения
- 32. Уравнение кардиоиды.
- 33. Заключение. Школьный курс геометрии полностью основан на
- 34. Заключение.Работая над рефератом, я расширила свой кругозор,
- 35. Скачать презентанцию
Введение. При написании реферата я поставила перед собой задачу познакомиться с параметрическими уравнениями кривых, полярными координатами, заданием кривых уравнениями в полярных координатах. Для этого я изучила циклоидальные кривые: кардиоиду, астроиду, нефроиду
Слайды и текст этой презентации
Слайд 3Введение.
Металлическая пластинка с профилем в виде половины витка архимедовой спирали
часто используется в конденсаторе переменной емкости. Одна из деталей швейной
машины – механизм для равномерного наматывания ниток на шпульку – имеет форму спирали Архимеда. Что касается логарифмической спирали, то вращающиеся ножи нередко имеют профиль, очерченный по логарифмической спирали, что позволяет сохранять при вращении постоянный угол резания и благодаря чему лезвие ножа стачивается равномерно. В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины, благодаря чему напор воды используется с наибольшей производительностью.Слайд 4Введение.
Разнообразные задачи из физики и математики, связанные с этими
кривыми, послужили пробным камнем для мощных аналитических методов, созданных в
веке Декартом, Лейбницем, Ньютоном, Ферма и другими учеными.В своей работе я применяла энциклопедии, популярные лекции по математике, учебники для физико-математических школ, научно- популярные журналы.
Слайд 14Полярные координаты.
Полярными координатами точки А на плоскости с заданной
полярной осью называется пара (r;φ), где r – расстояние от
точки А до точки О, φ – угол между полярной осью и вектором АО, отсчитываемый в направлении против часовой стрелки, если φ>0, и по часовой стрелке, если φ<0.При этом первая координата r называется полярным радиусом, а вторая φ – полярным углом. Полярный угол φ можно задавать в градусах или радианах.
Слайд 22Спираль Архимеда.
Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний
между соседними витками. Каждое из них равно 2аπ. Действительно, если
угол φ увеличивается на 2π, то есть точка делает один оборот против часовой стрелки, то радиуса на 2πа, что и составляет расстояние между соседними витками.Слайд 27Циклоида.
Рассмотрим циклоиду – кривую, которая описывается точкой, закрепленной на окружности
радиуса R, тогда эта окружность катится по оси Ох.
Слайд 31Кардиоида.
Кардиоида – кривая, являющаяся траекторией движения точки, закрепленной на
окружности, катящейся по окружности того же радиуса.
Слайд 33Заключение.
Школьный курс геометрии полностью основан на геометрии Евклида, в
которой изучаются свойства прямолинейных фигур и окружности. Основную роль
играют построения, вычисления же, хотя практическое значение их и велико, в теории играют подчиненную роль. Выбор того или иного построения обычно требует изобретательности. Это и составляет главную трудность при решении задач.Современный мир можно познать, применяя различные геометрии:
Лобачевского, аффинную и т.д. Одним из направлений геометрии является аналитическая геометрия. Она возникла из потребности создать единообразные средства для решения геометрических задач с тем, чтобы применить их к изучению важных для практики кривых линий различной формы.
Слайд 34Заключение.
Работая над рефератом, я расширила свой кругозор, приобрела навыки работы
с параметрическими уравнениями. Аналитическая геометрия тесно связана со всеми науками,
особенно с биологией и физикой. Например, цветки и листы любых растений, сложные траектории движения планет или каких – либо других физических тел можно описать с помощью уравнений кривых в полярных координатах.Материал достаточно сложный, в школе мы подобных тем не изучаем, поэтому я научилась работать с научной литературой. Все предметы, которые мы изучаем в школе, взаимосвязаны. Таким образом, только изучая их в комплексе, можно понять целостность окружающего нас мира.