Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двугранный угол
Содержание
- 1. Двугранный угол
- 2. Основные задачи урока:Ввести понятие двугранного угла и
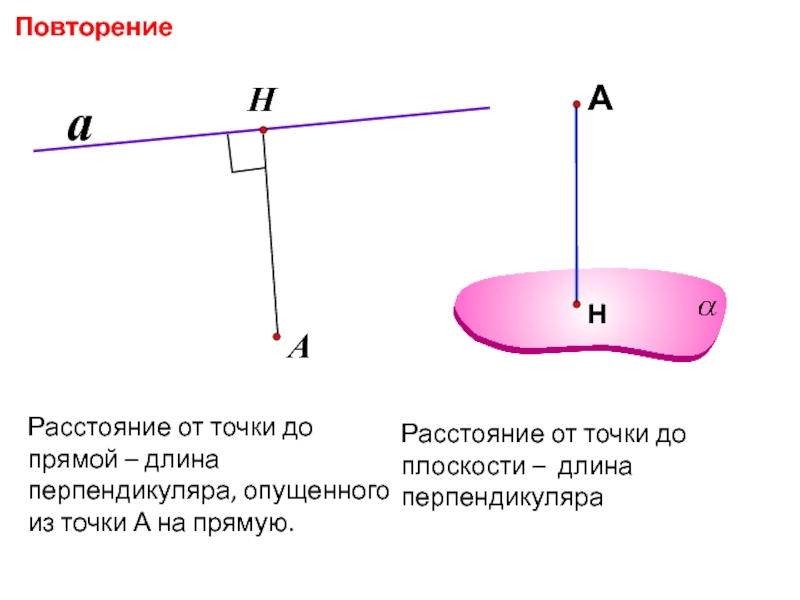
- 3. Расстояние от точки до прямой – длина
- 4. ВСMИз точки В к плоскости проведена наклонная,
- 5. ВСMАИз точки В к плоскости проведены две
- 6. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 7. Двугранным углом называется фигура, образованная прямой a
- 8. Величиной двугранного угла называется величина его линейного
- 9. Все линейные углы двугранного угла равны друг
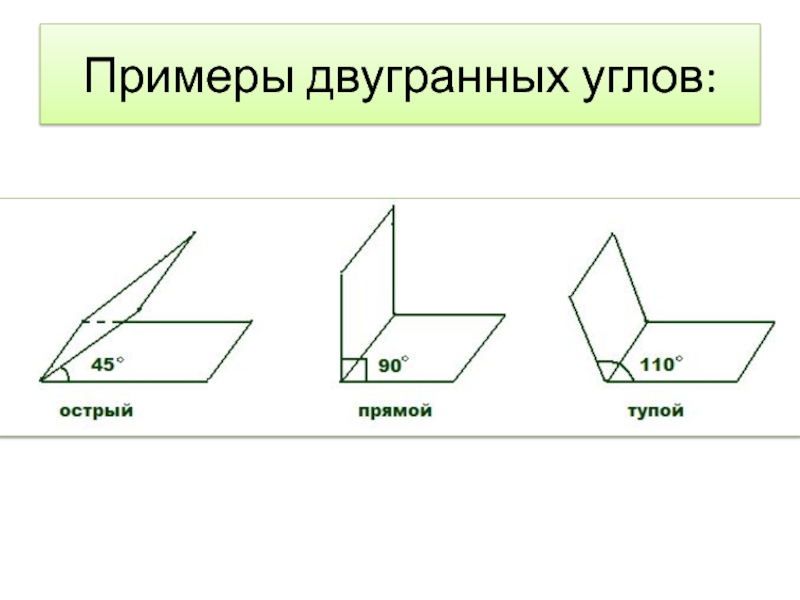
- 10. Примеры двугранных углов:
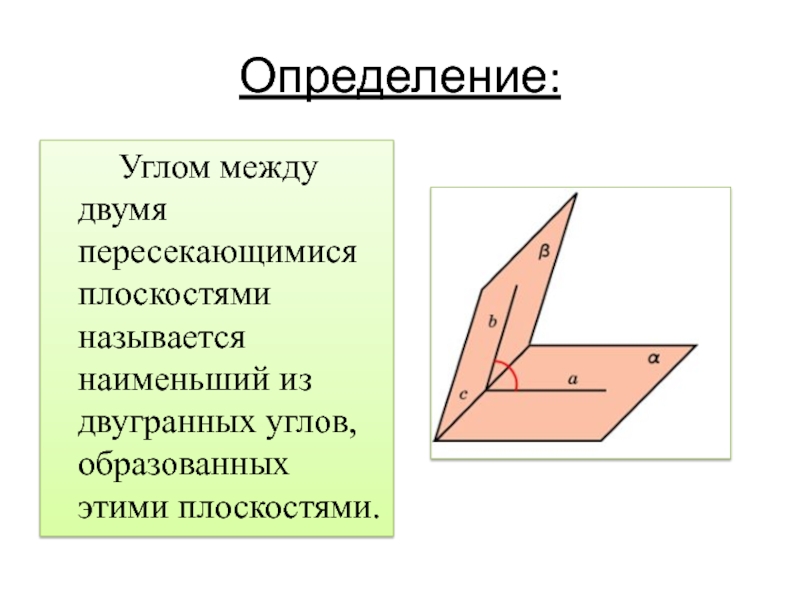
- 11. Определение: Углом между двумя
- 12. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
- 13. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
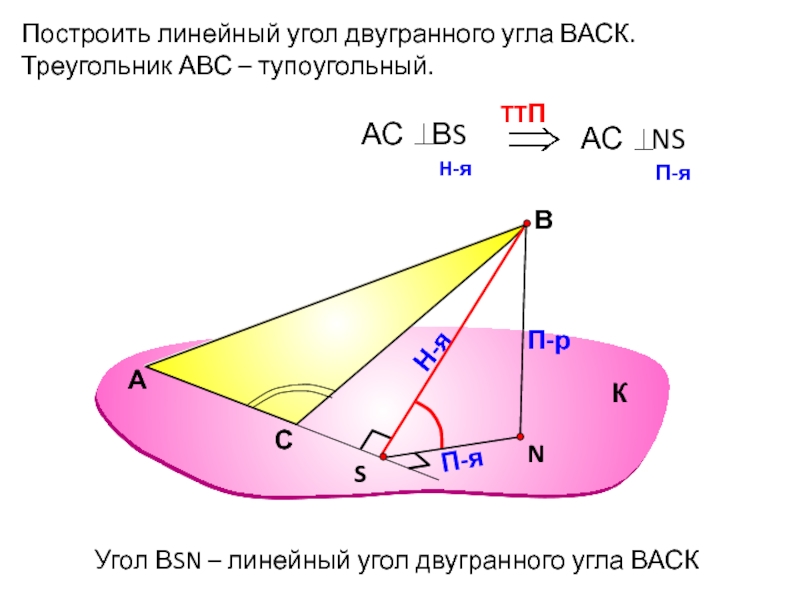
- 14. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
- 15. Задача 5:В кубе A…D1 найдите угол между
- 16. Домашнее задание:Параграф 3, п.22, №167, 169, с.57, вопросы 7-10.
- 17. Скачать презентанцию
Основные задачи урока:Ввести понятие двугранного угла и его линейного углаРассмотреть задачи на применение этих понятийСформировать конструктивный навык нахождения угла между плоскостями
Слайды и текст этой презентации
Слайд 2Основные задачи урока:
Ввести понятие двугранного угла и его линейного угла
Рассмотреть
задачи на применение этих понятий
плоскостями
Слайд 3Расстояние от точки до прямой – длина перпендикуляра, опущенного из
точки А на прямую.
a
А
Расстояние от точки до плоскости – длина
перпендикуляраПовторение
А
Слайд 4В
С
M
Из точки В к плоскости проведена наклонная, равная 12 см.
Угол между наклонной и ее проекцией на плоскость равен 300.
Найти расстояние от точки В до плоскости.12 см
300
?
Слайд 5В
С
M
А
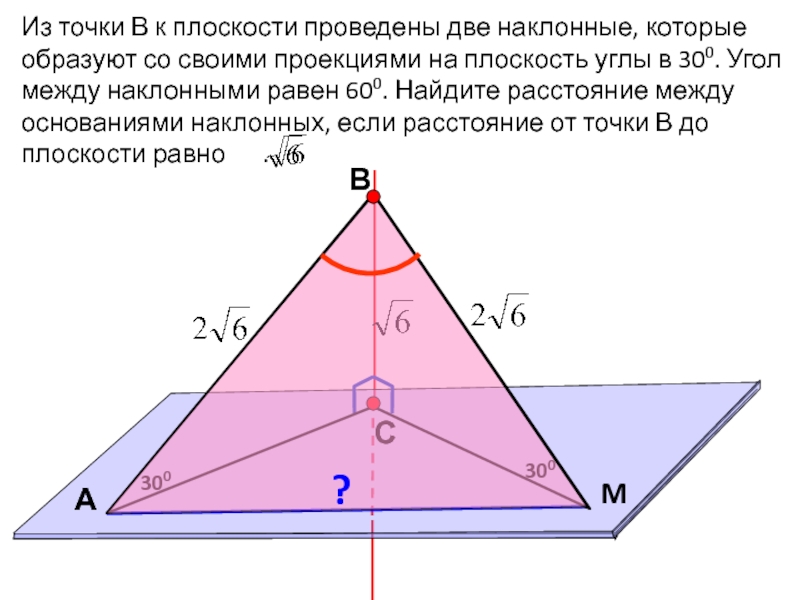
Из точки В к плоскости проведены две наклонные, которые образуют
со своими проекциями на плоскость углы в 300. Угол между
наклонными равен 600. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно .300
300
?
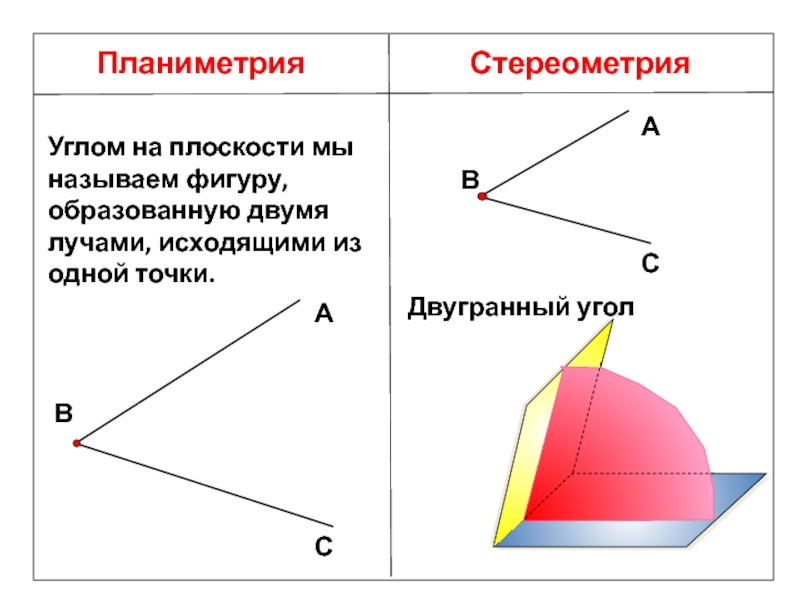
Слайд 6Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими
из одной точки.
Двугранный угол
Слайд 7Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями
с общей границей a, не принадлежащими одной плоскости.
Две полуплоскости –
грани двугранного углаПрямая a – ребро двугранного угла
a
Слайд 8Величиной двугранного угла называется величина его линейного угла.
AF ⊥ CD
BF ⊥ CDAFB-линейный угол двугранного угла ACDВ
Слайд 9Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и
О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы
АОВ и А1О1В1 равны, как углы с сонаправленными сторонами
Слайд 11Определение:
Углом между двумя пересекающимися плоскостями называется
наименьший из двугранных углов, образованных этими плоскостями.
Слайд 12Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN
– линейный угол двугранного угла ВАСК
К
Слайд 13Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN
– линейный угол двугранного угла ВАСК
К
С
Слайд 14Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN
– линейный угол двугранного угла ВАСК
К
С
Слайд 15Задача 5:
В кубе A…D1 найдите угол между плоскостями
BC1D и BA1D.
Решение:
Пусть
О – середина ВD. A1OC1 – линейный угол двугранного угла
А1ВDС1.
