Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники. Призма
Содержание
- 1. Многогранники. Призма
- 2. Многогранник – это тело, поверхность которого состоит из конечного числа плоских многоугольников.
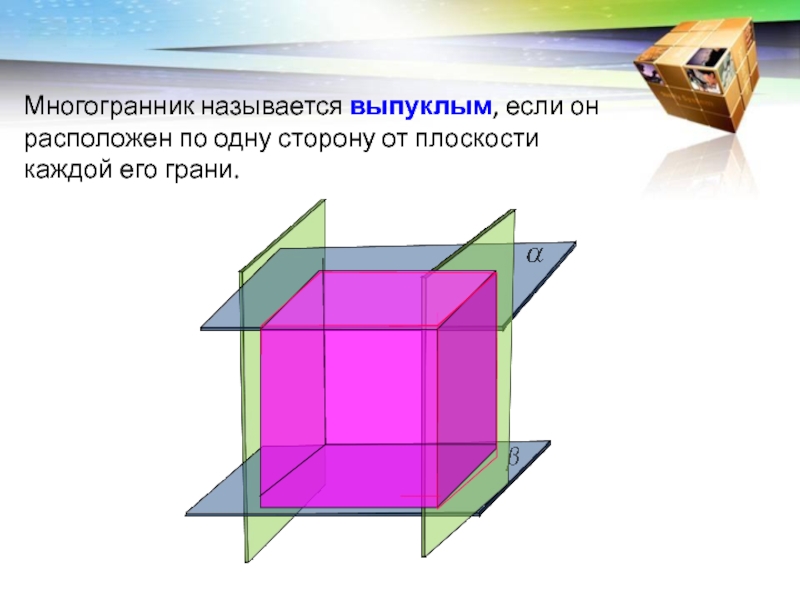
- 3. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
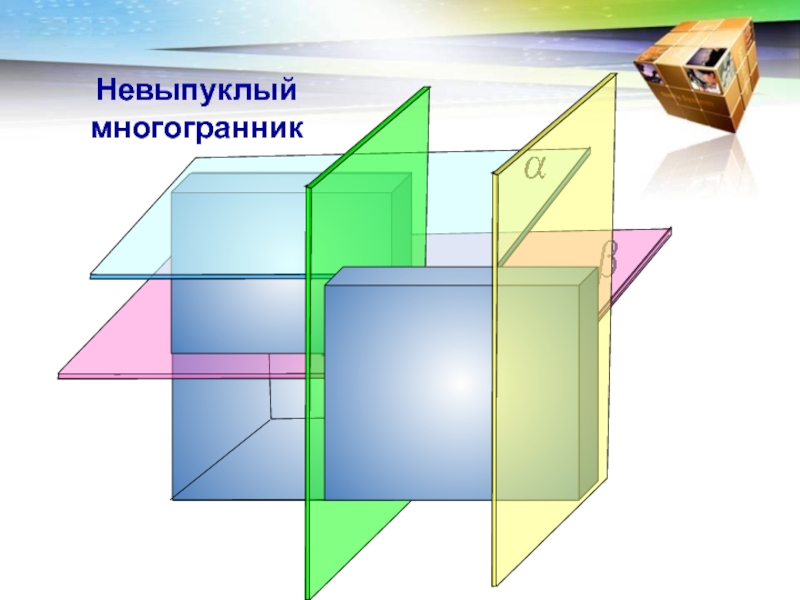
- 4. Невыпуклый многогранник
- 5. ПризмаПризма - многогранник, который состоит из двух
- 6. Свойства призмыОснования призмы равны.У призмы основания лежат
- 7. ПризмаПрямая НаклоннаяПрямая призма называется правильной, если ее основания являются правильными многоугольниками.
- 8. Боковой поверхностью призмы (площадью боковой поверхности) называется
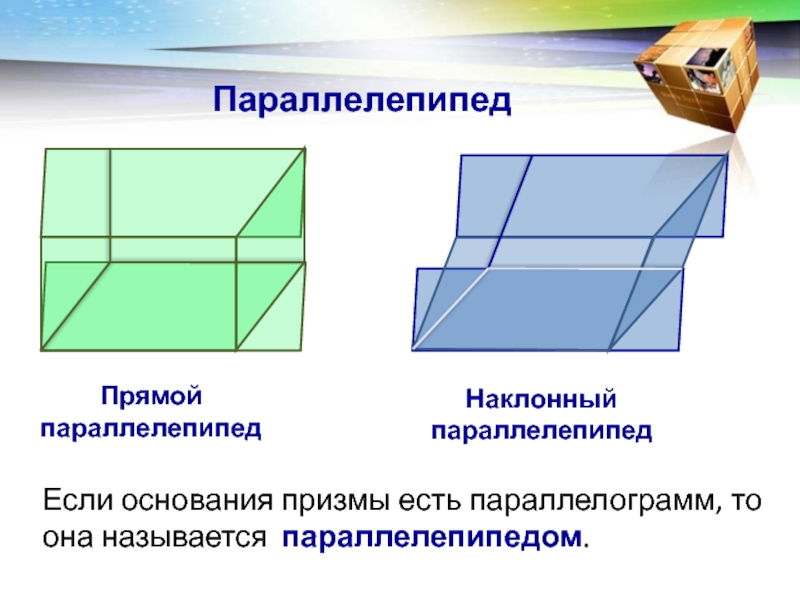
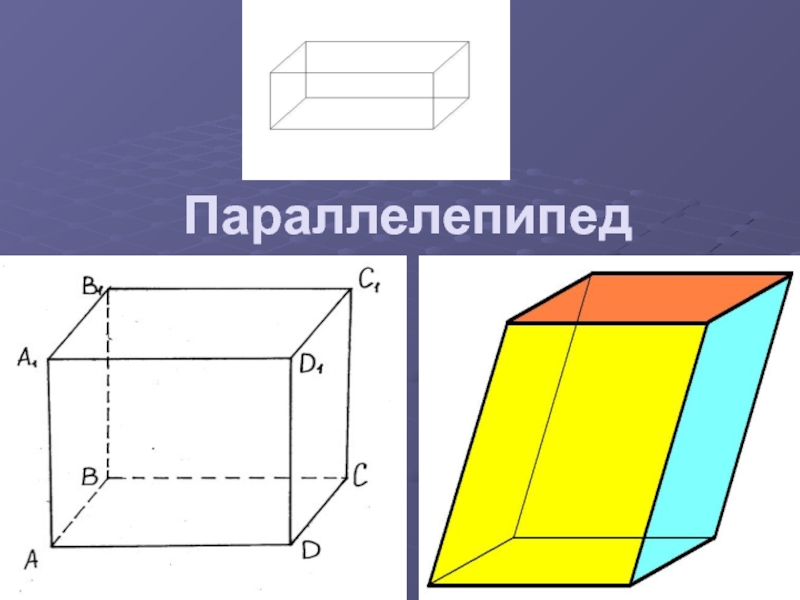
- 9. Параллелепипед Если основания призмы есть параллелограмм, то она называется параллелепипедом.Прямой параллелепипедНаклонный параллелепипед
- 10. Грани параллелепипеда, не имеющие общих вершин, называются
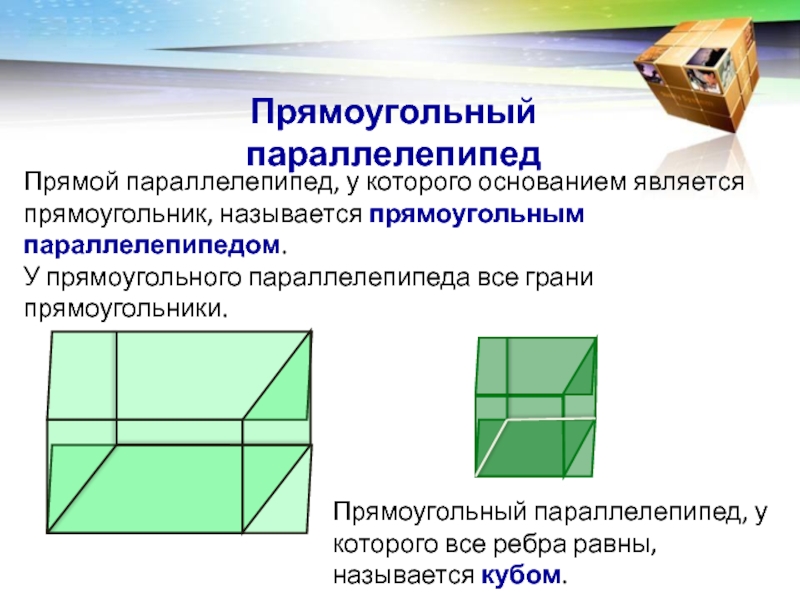
- 11. Прямоугольный параллелепипедПрямой параллелепипед, у которого основанием является
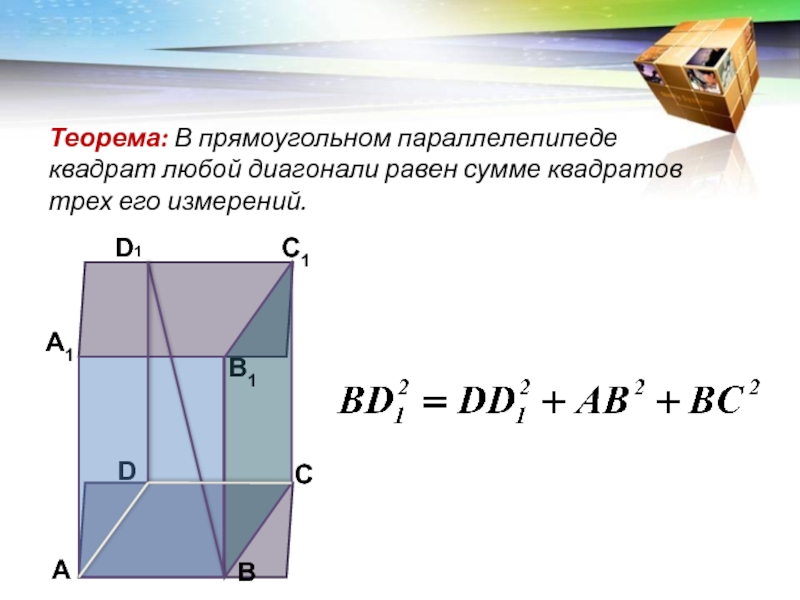
- 12. Теорема: В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.СА1С1В1DАD1В
- 13. Скачать презентанцию
Многогранник – это тело, поверхность которого состоит из конечного числа плоских многоугольников.
Слайды и текст этой презентации
Слайд 2Многогранник – это тело, поверхность которого состоит из конечного числа
плоских многоугольников.
Слайд 3Многогранник называется выпуклым, если он расположен по одну сторону от
плоскости каждой его грани.
Слайд 5Призма
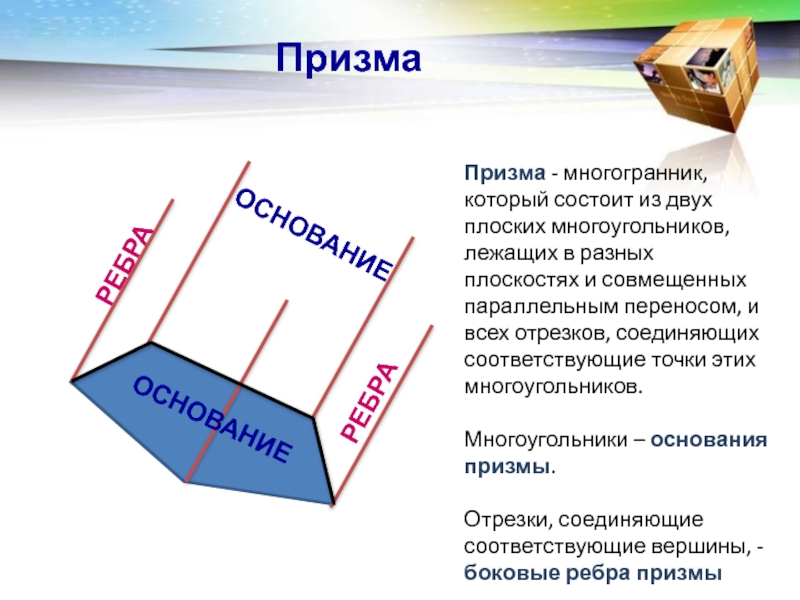
Призма - многогранник, который состоит из двух плоских многоугольников, лежащих
в разных плоскостях и совмещенных параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих многоугольников.Многоугольники – основания призмы.
Отрезки, соединяющие соответствующие вершины, - боковые ребра призмы
ОСНОВАНИЕ
ОСНОВАНИЕ
РЕБРА
РЕБРА
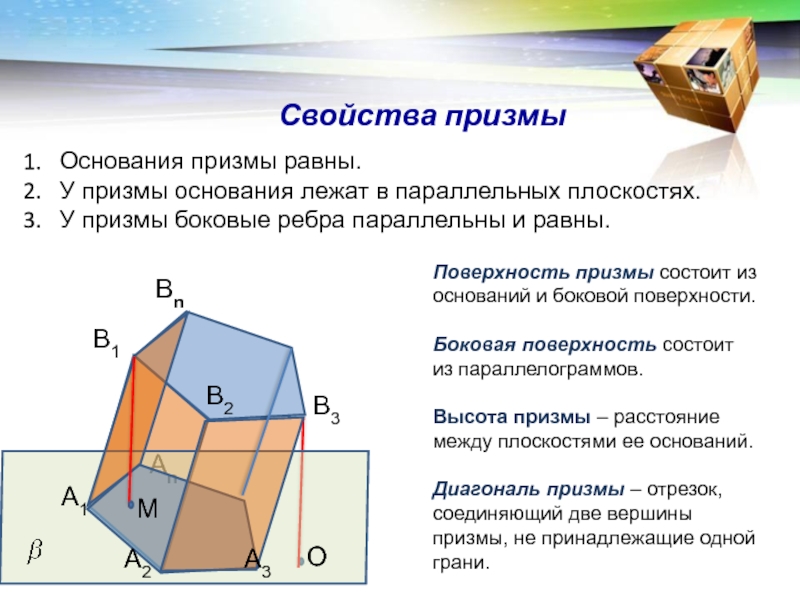
Слайд 6Свойства призмы
Основания призмы равны.
У призмы основания лежат в параллельных плоскостях.
У
призмы боковые ребра параллельны и равны.
Поверхность призмы состоит из оснований
и боковой поверхности.Боковая поверхность состоит из параллелограммов.
Высота призмы – расстояние между плоскостями ее оснований.
Диагональ призмы – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Аn
Слайд 7Призма
Прямая Наклонная
Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Слайд 8Боковой поверхностью призмы (площадью боковой поверхности) называется сумма площадей боковых
граней.
Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема:
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т.е. на длину бокового ребра.h
h
Pocн
Слайд 9Параллелепипед
Если основания призмы есть параллелограмм, то она называется параллелепипедом.
Прямой
параллелепипед
Наклонный параллелепипед
Слайд 10Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Теорема: У параллелепипеда
противолежащие грани параллельны и равны.
Теорема: Диагонали параллелепипеда пересекаются в
одной точке точкой пересечения делятся пополам.Следствие: точка пересечения диагоналей параллелепипеда является его центром.
Слайд 11Прямоугольный параллелепипед
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным
параллелепипедом.
У прямоугольного параллелепипеда все грани прямоугольники.
Прямоугольный параллелепипед, у которого все
ребра равны, называется кубом.
Слайд 12Теорема: В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов
трех его измерений.
С
А1
С1
В1
D
А
D1
В
