Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Содержание
- 1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 2. СодержаниеЦель Введение Понятие правильного многогранникаИсторическая справкаТетраэдрГексаэдрОктаэдрИкосаэдрДодекаэдрПравильные многогранники в архитектуре и живописиЗвездчатые многогранникиВывод
- 3. ЦЕЛЬ Познакомиться с новым типом выпуклых многогранников-правильными многогранниками.
- 4. ВВЕДЕНИЕПравильные многогранники известны с древнейших времён. Их
- 5. Понятие правильного многогранникаПравильный многогранник или платоново тело
- 6. Слайд 6
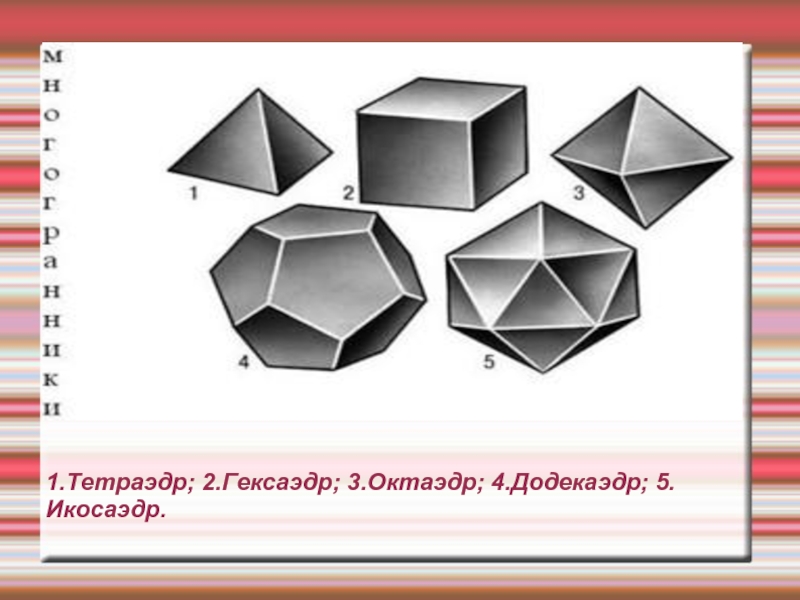
- 7. 1.Тетраэдр; 2.Гексаэдр; 3.Октаэдр; 4.Додекаэдр; 5.Икосаэдр.
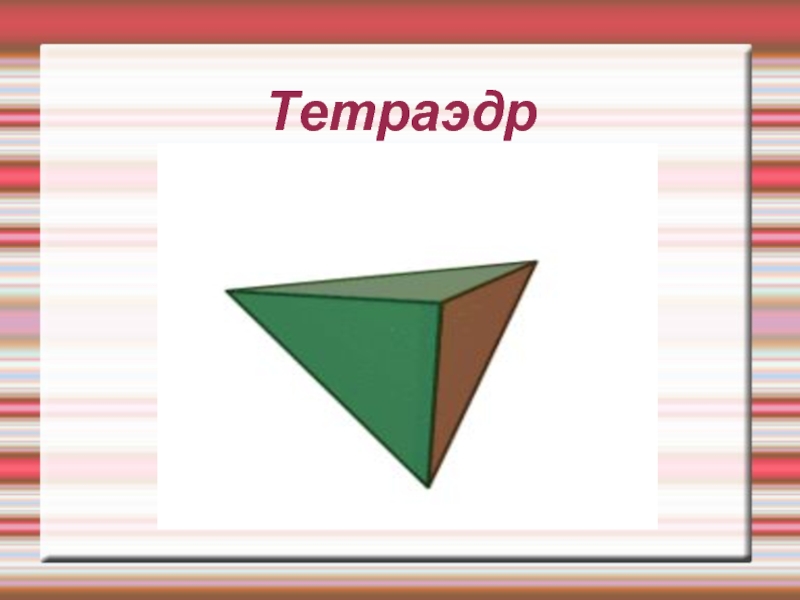
- 8. Тетраэдр
- 9. Определение:Тетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший
- 10. Тетраэдры в микромиреМолекула метана СН4Молекула аммиака NH3Алмаз
- 11. Тетраэдры в природе Некоторые плоды, находясь вчетвером
- 12. Тетраэдры в техникеТетраэдр образует жёсткую, статически определимую
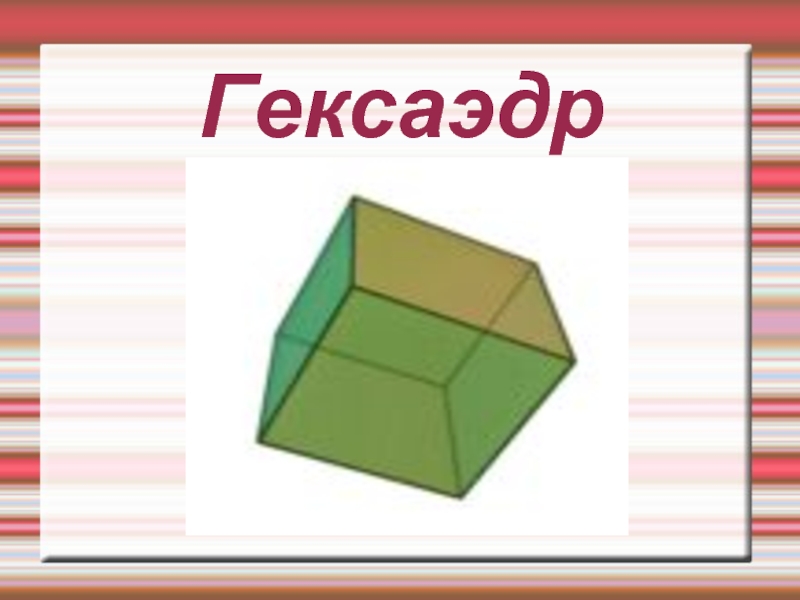
- 13. Гексаэдр
- 14. Определение:Куб или правильный гексаэдр — правильный многогранник,
- 15. ИГРАЛЬНЫЕ КОСТИ
- 16. КУБИК РУБИКА
- 17. КУБИК СОМА
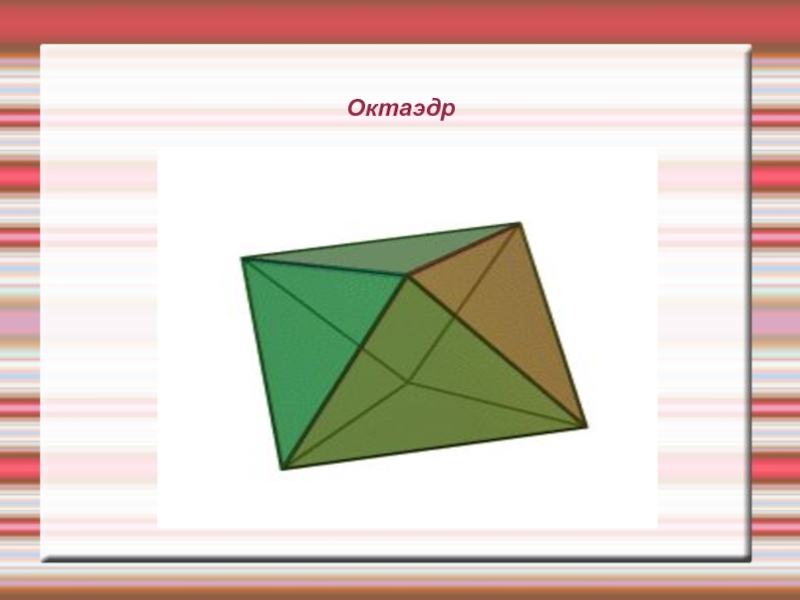
- 18. Октаэдр
- 19. Определение:Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь»
- 20. Октаэдр
- 21. Октаэдр в природе
- 22. Икосаэдр
- 23. Определение:Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение»,
- 24. Слайд 24
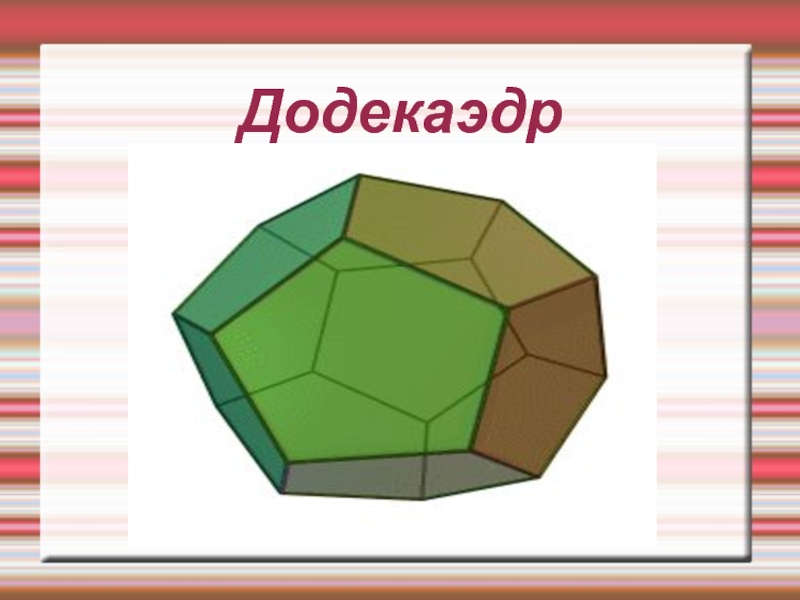
- 25. Додекаэдр
- 26. Определение:Додека́эдр (от греч. δώδεκα — двенадцать и
- 27. Слайд 27
- 28. Правильные многогранники в архитектуре и живописи
- 29. Слайд 29
- 30. Остров и маяк
- 31. Александровский маяк
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Звездчатые многогранникиПравильные звёздчатые многогранники — это звёздчатые
- 36. Слайд 36
- 37. Слайд 37
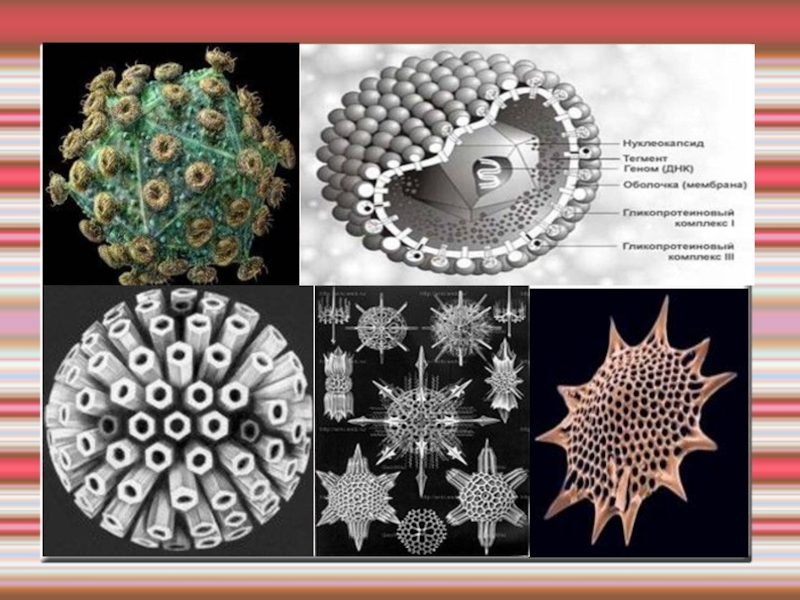
- 38. Живые многогранники
- 39. Слайд 39
- 40. ВЫВОДВыпуклый многогранник называется правильным, если его грани
- 41. СПАСИБО ЗА ВНИМАНИЕ!
- 42. Скачать презентанцию
СодержаниеЦель Введение Понятие правильного многогранникаИсторическая справкаТетраэдрГексаэдрОктаэдрИкосаэдрДодекаэдрПравильные многогранники в архитектуре и живописиЗвездчатые многогранникиВывод
Слайды и текст этой презентации
Слайд 1
Проектная работа
"Правильные многогранники"
Выполнила ученица 10 класса МКОУ "Калининская СОШ" Сигабатова
Асылай
Слайд 2Содержание
Цель
Введение
Понятие правильного многогранника
Историческая справка
Тетраэдр
Гексаэдр
Октаэдр
Икосаэдр
Додекаэдр
Правильные многогранники в архитектуре и
живописи
Звездчатые многогранники
Вывод
Слайд 4ВВЕДЕНИЕ
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно
найти на резных каменных шарах, созданных в период позднего неолита,
в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.
Слайд 5Понятие правильного многогранника
Правильный многогранник или платоново тело — это выпуклый
многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией
Примеры:
правильный гексаэдр(куб), правильный тетраэдр, правильный октаэдр, правильный икосаэдр, правильный додекаэдрСлайд 9Определение:
Тетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого
являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и
6 рёбер.Свойства:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части
Слайд 10Тетраэдры в микромире
Молекула метана СН4
Молекула аммиака NH3
Алмаз C — тетраэдр
с ребром равным 2,5220 ангстрем
Флюорит CaF2, тетраэдр с ребром равным
3, 8626 ангстремСфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4
Слайд 11Тетраэдры в природе
Некоторые плоды, находясь вчетвером
на одной кисти,
располагаются в вершинах
тетраэдра, близкого к правильному. Такая
конструкция обусловлена
тем, что центрычетырёх одинаковых шаров, касающихся
друг друга, находятся в вершинах
правильного тетраэдра. Поэтому похожие
на шар плоды образуют подобное
взаимное расположение. Например,
таким образом могут располагаться
грецкие орехи.
Слайд 12Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный
из стержней, часто используется в качестве основы для пространственных несущих
конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр.
Слайд 14
Определение:
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого
представляет собой квадрат.
Свойства:
Четыре сечения куба являются правильными шестиугольниками — эти
сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Слайд 19
Определение:
Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα
— «основание») — один из пяти выпуклых правильных многогранников, так
называемых Платоновых тел.Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Свойства:
Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
Правильный октаэдр имеет симметрию Oh, совпадающую с симметрией куба.
Слайд 23Определение:
Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение», «основание») — правильный
выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20
граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.Свойства:
Икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, так что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.
Собрать модель икосаэдра можно при помощи 20 тетраэдров.
Слайд 26Определение:
Додека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань)
— двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра
является вершиной трёх правильных пятиугольников.Свойство:
В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.
Слайд 35Звездчатые многогранники
Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых
являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует
всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера — Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера — Пуансо.Слайд 40ВЫВОД
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками
с одним и тем же числом сторон, и в каждой
вершине многогранника сходится одно и то же число ребер.Правильный тетраэдр (четырехгранник) — многогранник, составленный из четырех правильных треугольников.
Правильный гексаэдр (шестигранник) или куб — многогранник, составленный из шести правильных четырехугольников (квадратов).
Правильный октаэдр (восьмигранник) — многогранник, составленный из восьми правильных треугольников.
Правильный додекаэдр (двенадцатигранник) — многогранник, составленный из двенадцати правильных пятиугольников
Правильный икосаэдр (двадцатигранник) — многогранник, составленный из двадцати правильных треугольников.
Теги