Скажи мне — и я забуду, покажи мне — и я запомню, дай мне сделать — и я пойму.
Конфуций
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование подобия
Содержание
- 1. Преобразование подобия
- 2. Конфуцийдревний мыслитель, философ Китая
- 3. ОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПОВОРОТДВИЖЕНИЕ
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Свойства движения:При движении прямая переходит в прямую,
- 9. Что такое подобие и где оно встречается?Посмотрите на эту картинку.
- 10. . Все матрешки имеют одинаковое лицо, костюмы
- 11. Где встречается подобие? Посмотрите вокруг.Мы живем в
- 12. Вот некоторые подобия которые встречаем мы в
- 13. В геометрии фигуры одинаковой формы
- 14. А для чего нам нужно подобие?Для решения
- 15. Отойдя на некоторое расстояние от дерева,
- 16. Подобие фигурПреобразование фигуры F в фигуру F'
- 17. Свойства подобияПодобие сохраняет порядок точек на прямой,
- 18. ГомотетияЗафиксируем точку O и положительное число k.
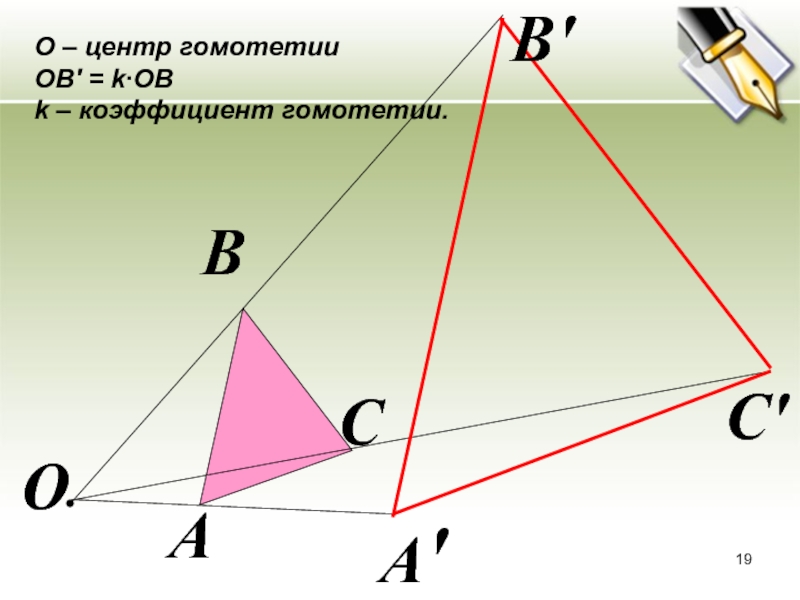
- 19. О – центр гомотетииОВ′ = k∙ОВk – коэффициент гомотетии.ОАА′ВВ′СС′
- 20. Рассмотрим случаи:1 случай: k > 0 а)
- 21. Дано: ∆АВС,О – центр гомотетии,k = 3.Построить:
- 22. 1 случай: б) k = 1/3 АВСОА′В′С′ОА′
- 23. 2 случай: k = -2ОАВСА′В′С′ОА′ = |-2|∙ОА
- 24. Подобными являются любые два круга, два квадрата.
- 25. Подобие фигур.
- 26. ЕСЛИ ФИГУРА F1 ПОДОБНА ФИГУРЕ F2, А
- 27. Преобразование подобия имеет широкое практическое применение, в
- 28. Подобие в жизни(карты местности)
- 29. Преобразование подобияПреобразование одной фигуры в другую называется
- 30. Пример преобразования подобияРасстояние между соответствующими точками изменилось
- 31. Задание 1Квадрат F1 был подвергнут некоторому преобразованию.
- 32. Подобные треугольники:АВСДва треугольника называются подобными, если их
- 33. Подобные треугольники:∆КМР∆СОВНайдите равные углыНазовите пропорциональные стороныI вариант∆DEO∆NRMII вариант∆СВР∆КМО
- 34. Скачать презентанцию
Конфуцийдревний мыслитель, философ Китая
Слайды и текст этой презентации
Слайд 1Преобразование подобия.
Слайд 8Свойства движения:
При движении прямая переходит в прямую, луч – в
луч, отрезок – в отрезок.
Сохраняются расстояния между точками.
Сохраняются углы между
лучами.
Слайд 10.
Все матрешки имеют одинаковое лицо,
костюмы и пропорции. Значит
они являются
ПОДОБНЫМИ ФИГУРАМИ. Что такое подобные фигуры? Простым языком
Это те фигуры, которые
имеют разные массы, размеры, но
одинаковые формы!
Слайд 11Где встречается подобие?
Посмотрите вокруг.
Мы живем в мире подобия. В самом
Человеке заложен Принцип Подобия, каждый его орган или часть тела
подобна всему телу. Даже все люди похожи. У каждого из нас одинаковый набор органов. У каждого два уха, два глаза и тп.Мы живем на планете Земля, наша планета подобна другим планетам. Она такая же круглая как и все планеты во вселенной.
Слайд 12Вот некоторые подобия которые встречаем мы в жизни:
Посмотрите на рисунке
4 вида мячей. Они все имеют разные размеры и массы,
но одинаковую форму - круга.
Слайд 14А для чего нам нужно подобие?
Для решения задач. А вы
знали, что при помощи зеркала можно найти высоту рядом находящегося
предмета. Как измерить высоты дерева с которым мы стоим рядом?
Слайд 15 Отойдя на некоторое расстояние от дерева, зеркало следует положить
на землю так, чтобы оно приняло горизонтальное положение. Затем нужно
постепенно отходить назад до тех пор, пока в зеркале удастся увидеть отражение вершины дерева.Высота дерева будет во столько раз больше роста человека (до высоты глаз), во сколько расстояние от зеркала до дерева больше расстояние от зеркала до места стояния человека .
Слайд 16Подобие фигур
Преобразование фигуры F в фигуру F' называется преобразованием подобия,
если при этом преобразовании расстояния между точками изменяются в одно
и то же число раз.Две фигуры F и F' называются подобными, если одна из них переводится в другую подобием.
F
F'
Y
Х
Y'
Х'
Х Х'
Y Y'
Х'Y' = k ХY
число k называется коэффициентом подобия.
Слайд 17Свойства подобия
Подобие сохраняет порядок точек на прямой, то есть если
точка лежит между точками — соответствующие их образы при некотором
подобии, то также лежит между точками.Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой.
Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.
При подобии угол сохраняет величину.
Подобие с коэффициентом , преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом.
Каждое подобие можно рассматривать как композицию движения и некоторой гомотетии с положительным коэффициентом.
Подобие называется собственным (несобственным), если движение является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную.
Два треугольника являются подобными, если их соответственные углы равны, или стороны пропорциональны.
Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).
Преобразование подобия сохраняет углы между полупрямыми.
Слайд 18Гомотетия
Зафиксируем точку O и положительное число k. Каждой точке Х
плоскости, отличной от O сопоставим точку Х' на луче OХ
так, что OХ' = k OХ. Точке O сопоставим ее саму.O
Х
Х'
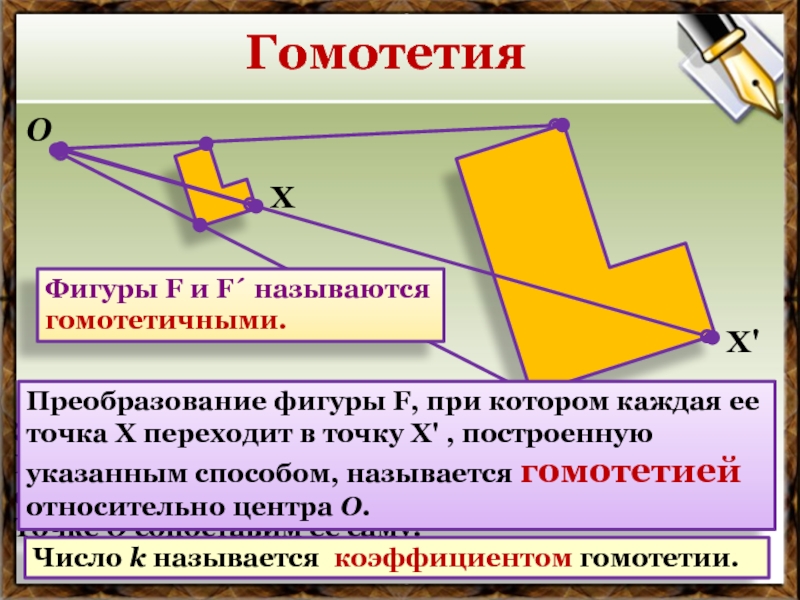
Преобразование фигуры F, при котором каждая ее точка Х переходит в точку Х' , построенную указанным способом, называется гомотетией относительно центра O.
Число k называется коэффициентом гомотетии.
Фигуры F и F´ называются гомотетичными.
Слайд 21Дано: ∆АВС,
О – центр гомотетии,
k = 3.
Построить: ∆А´В´С´, гомотетичный ∆АВС.
Построение.
А
В
С´
А´
В´
С
Проведем луч ОА.
Отложим на нем
отрезок ОА´ = 3 ∙ОА.Проведем луч ОС.
Проведем луч ОВ.
Отложим на нем отрезок ОС´ = 3 ∙ОС.
Отложим на нем отрезок ОВ´ = 3 ∙ОВ.
Достроим ∆А´В´С´ - искомый.
О
Построение фигуры
гомотетичной данной
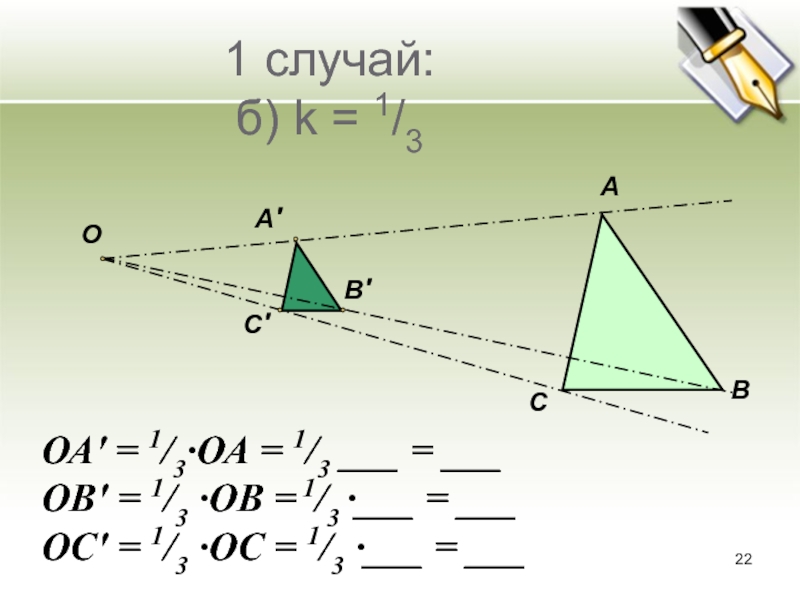
Слайд 221 случай:
б) k = 1/3
А
В
С
О
А′
В′
С′
ОА′ = 1/3∙ОА = 1/3
___ = ___
ОВ′ = 1/3 ∙ОВ = 1/3 ∙___ =
___ОС′ = 1/3 ∙ОС = 1/3 ∙___ = ___
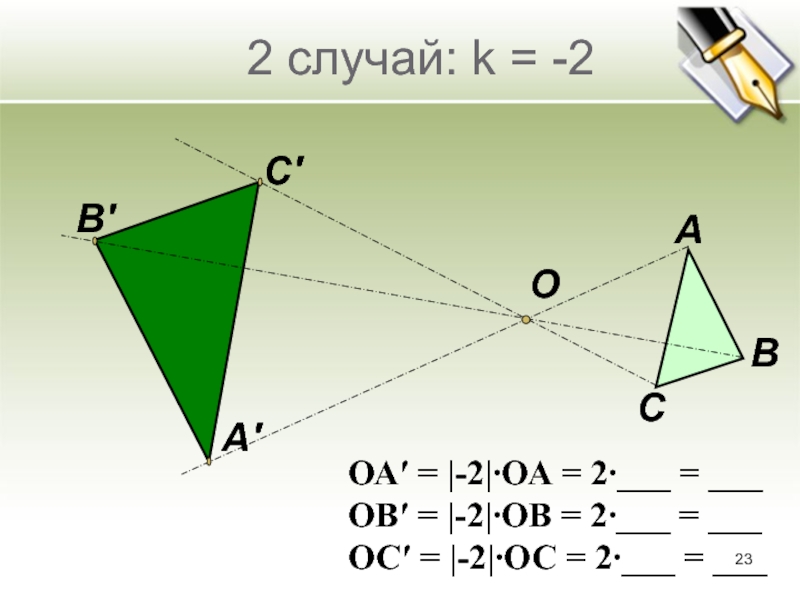
Слайд 232 случай: k = -2
О
А
В
С
А′
В′
С′
ОА′ = |-2|∙ОА = 2∙___ =
___
ОВ′ = |-2|∙ОВ = 2∙___ = ___
ОС′ = |-2|∙ОС =
2∙___ = ___
Слайд 27Преобразование подобия имеет широкое практическое применение, в частности, при выполнении
деталей машин, составлении карт и планов местности. При этом коэффициент
подобия называется масштабом.
Слайд 29Преобразование подобия
Преобразование одной фигуры в другую называется преобразованием подобия, если
при этом преобразовании расстояние между точками изменится в одно и
то же число разПроверь себя
Свойства преобразования подобия
Задание 1
Задание 2
Иллюстрация определения
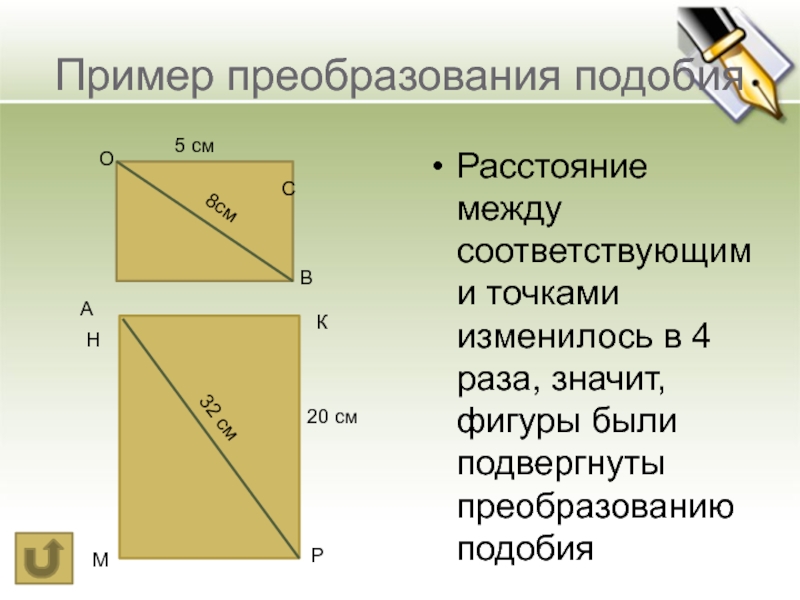
Слайд 30Пример преобразования подобия
Расстояние между соответствующими точками изменилось в 4 раза,
значит, фигуры были подвергнуты преобразованию подобия
А
Н
О
В С
К
Р
М
8см
5 см
32 см
20 см
Слайд 31Задание 1
Квадрат F1 был подвергнут некоторому преобразованию. В результате была
получена фигура F2. Будет ли данное преобразование являться преобразованием подобия?
Свой ответ обоснуйте.F1
F2
Слайд 32Подобные треугольники:
А
В
С
Два треугольника называются подобными, если их углы соответственно равны
и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
Стороны АВ
и А1В1ВС и В1С1
СА и С1А1 называются сходными
А1
Слайд 33Подобные треугольники:
∆КМР∆СОВ
Найдите равные углы
Назовите пропорциональные стороны
I вариант
∆DEO∆NRM
II вариант
∆СВР∆КМО
