Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение планиметрических задач высокого уровня сложности 9 класс
Содержание
- 1. Решение планиметрических задач высокого уровня сложности 9 класс
- 2. ЗАДАЧА №1Углы при одном из оснований трапеции
- 3. РЕШЕНИЕ ЗАДАЧИ №1Продолжим прямые AB и CD
- 4. Докажем, что отрезок, соединяющий середины оснований, равен
- 5. ДалееPM = CK = 1/2 (AD -
- 6. ЗАДАЧА №2Биссектрисы углов A и B при
- 7. ПЛАН РЕШЕНИЯ ЗАДАЧИ №21. Доказать, что AFB
- 8. ЗАДАЧА №3В параллелограмме ABCD длина диагонали BD
- 9. РЕШЕНИЕ ЗАДАЧИ №3BC – касательная к окружности,
- 10. Итак, BK – медиана и высота треугольника
- 11. Скачать презентанцию
ЗАДАЧА №1Углы при одном из оснований трапеции равны 23° и 67°, а отрезки, соединяющие середины противоположных сторон, равны 15 и 8. Найдите основания трапеции.
Слайды и текст этой презентации
Слайд 1РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ ВЫСОКОГО УРОВНЯ СЛОЖНОСТИ
МАОУ «Белоевская СОШ»
Автор:
Батина Надежда Ивановна
учитель математики высшей категории
Слайд 2ЗАДАЧА №1
Углы при одном из оснований трапеции равны 23° и
67°, а отрезки, соединяющие середины противоположных сторон, равны 15 и
8. Найдите основания трапеции.Слайд 3РЕШЕНИЕ ЗАДАЧИ №1
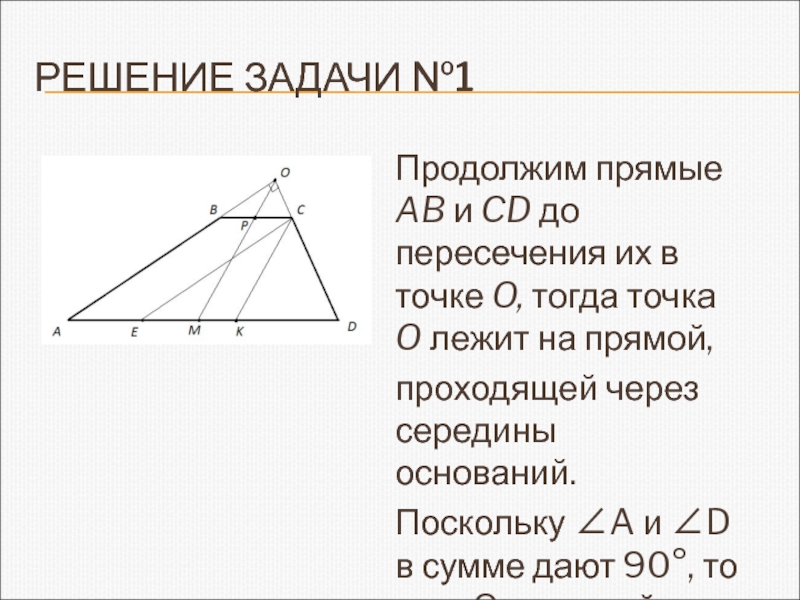
Продолжим прямые AB и CD до пересечения их
в точке O, тогда точка O лежит на прямой,
проходящей
через середины оснований. Поскольку ∠A и ∠D в сумме дают 90°, то угол O – прямой.
Слайд 4Докажем, что отрезок, соединяющий середины оснований, равен полуразности длин оснований.
Проведем
через точку С прямые CE и CK, параллельные AB
и OM соответственно, тогда CK – медиана прямоугольного треугольника ECD, поэтомуCK = 1/2 ED = 1/2 (AD - BC).
Из условия задачи PM=8, а средняя линия трапеции 15.
Слайд 5Далее
PM = CK = 1/2 (AD - BC) = 8;
1/2
(AD + BC) = 15.
Решая полученную систему, имеем:
BC = 7,
AD=23.
Ответ: 7 и 23.
Слайд 6ЗАДАЧА №2
Биссектрисы углов A и B при боковой стороне AB
трапеции ABCD пересекаются в точке F. Биссектрисы углов C и
D пересекаются в точке G. Найдите FG, если средняя линия равна 21, боковые стороны 13 и 15.Слайд 7ПЛАН РЕШЕНИЯ ЗАДАЧИ №2
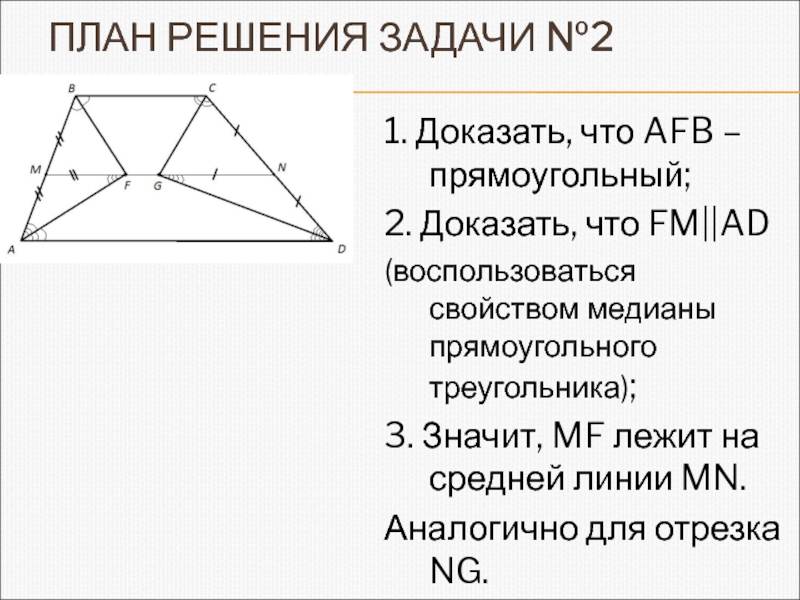
1. Доказать, что AFB –прямоугольный;
2. Доказать, что
FM||AD
(воспользоваться свойством медианы прямоугольного треугольника);
3. Значит, MF лежит на
средней линии MN.Аналогично для отрезка NG.
4. FG = MN – 1/2 AB – 1/2 CD
Ответ: FG=7.
Слайд 8ЗАДАЧА №3
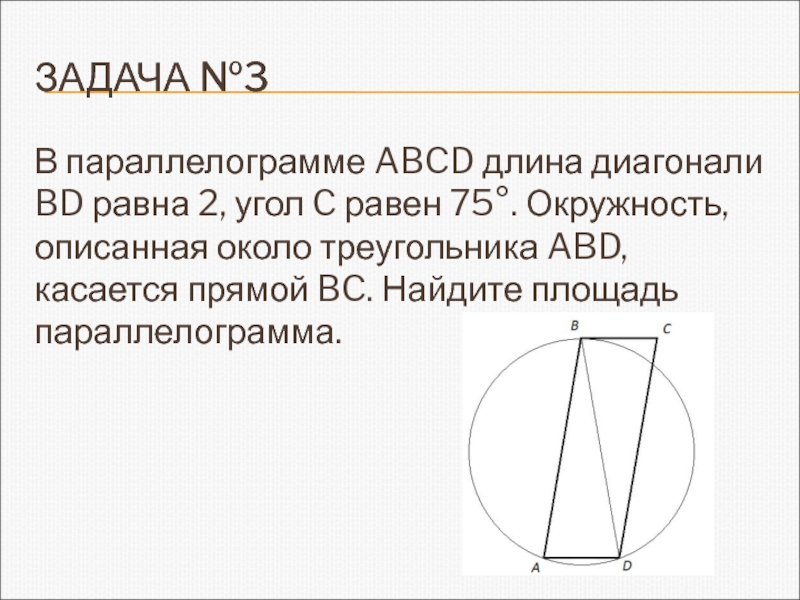
В параллелограмме ABCD длина диагонали BD равна 2, угол
C равен 75°. Окружность, описанная около треугольника ABD, касается прямой
BC. Найдите площадь параллелограмма.Слайд 9РЕШЕНИЕ ЗАДАЧИ №3
BC – касательная к окружности, описанной около треугольника
ABD. Пусть O – центр этой окружности, тогда OB⊥BC, значит
OB⊥AD. Хорда AD перпендикулярна к диаметру,значит, AK = KD.
Слайд 10Итак, BK – медиана и высота треугольника ABD, поэтому AB
= BD = 2.
∠A = ∠D = 75°, значит,
∠B = 30°
Площадь параллелограмма
в два раза больше площади треугольника ABD, следовательно:
S = AB · BD · sin 30° = 2
Ответ: 2.