Объём конуса

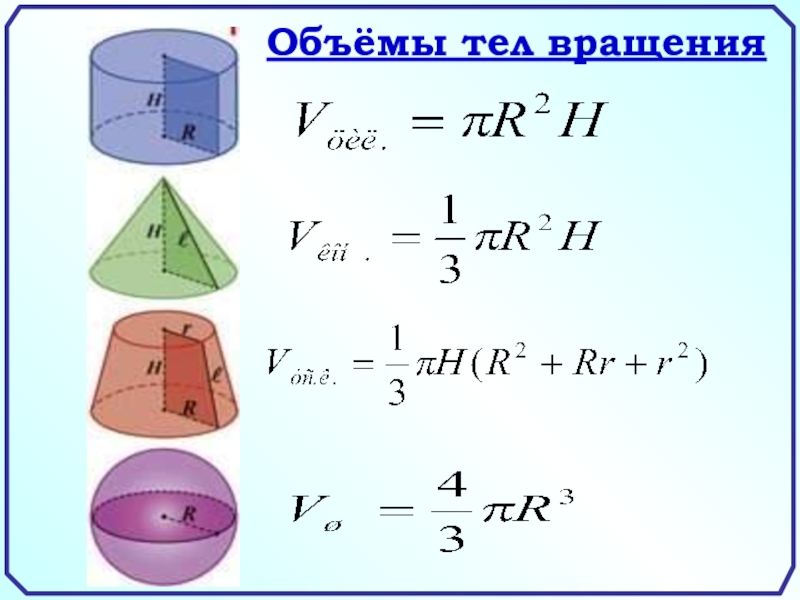
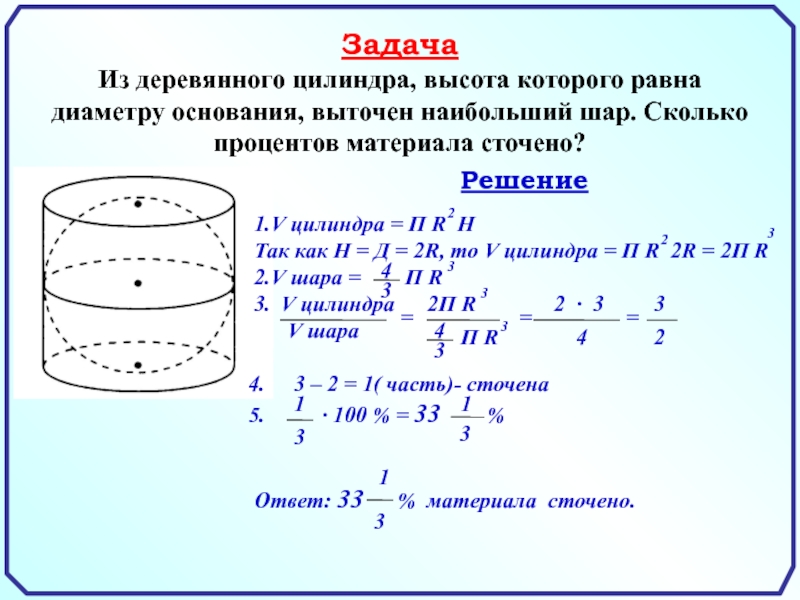
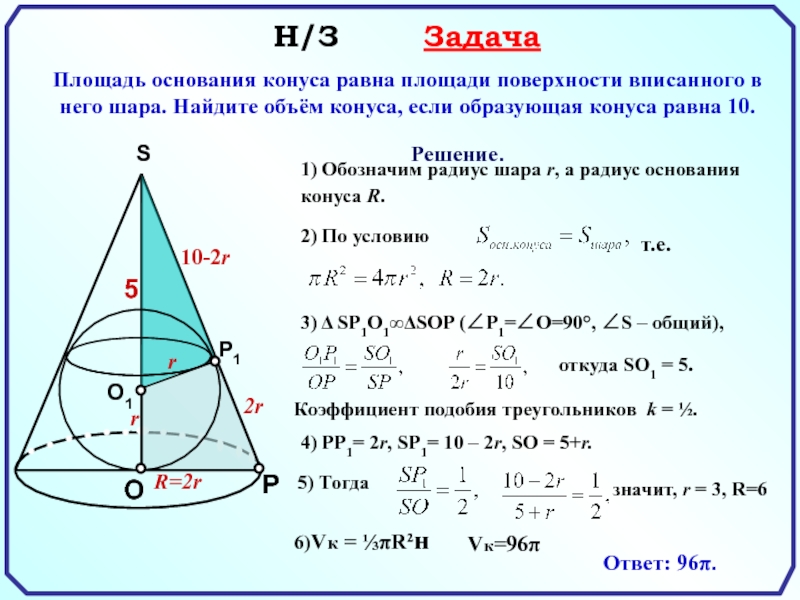
наибольший шар. Сколько процентов материала сточено?

Решение





1.V цилиндра =

П R Н
Так как Н = Д = 2R, то V цилиндра = П R 2R = 2П R
2.V шара = П R
3.


3 – 2 = 1( часть)- сточена
∙ 100 % = 33 %


Ответ: 33 % материала сточено.

2

2

3

3

4

3

V цилиндра

V шара

= = =

2П R 2 ∙ 3 3

3

4

3

П R 4 2

3

1

3

1

3

1

3

2:3.

задач

применять знания на практике

Аристотель

часы Древнего Египта (клепсидра)




Сосуд,
имеющий форму конуса, наполненный водой,

которая вытекала через отверстие в нижней его части. Уровень воды показывал время, истекшее с момента наполнения сосуда.

втулка,
сосновая шишка.

А
О Б Р А З

У Ю Щ А Я

О Б Ъ Ё М

Р А З В Ё Р Т К А

П Р Я М О Й

К Р У Г

О С Ь

Т Р Е У Г О Л Ь Н И К

Р А Д И У С

О С Е В О Е

Ш И Ш К А

1

2

3

4

5

6

7

8

9

10

11

2 раза, то его объём уменьшится в 2 раза.
2) Если

высоту конуса увеличить в 4 раза, то его объём увеличится в 4 раза.
3)Если радиус основания конуса увеличить
в 2 раза, а высоту уменьшить в 2 раза, то
объём конуса не изменится.
4)Если воду, заполняющую всю коническую колбу высотой 12 см, перелить в цилиндрический сосуд, радиус основания которого равен радиусу основания конической колбы, то высота, на которой будет находиться вода в цилиндрическом сосуде, будет равна 6 см.

2 раза, то его объём уменьшится в 4 раза.
2) Если

высоту конуса увеличить в 4 раза, то его объём увеличится в 4 раза.
3)Если радиус основания конуса увеличить
в 2 раза, а высоту уменьшить в 2 раза, то
объём конуса увеличится в 2 раза.
4)Если воду, заполняющую всю коническую колбу высотой 12 см, перелить в цилиндрический сосуд, радиус основания которого равен радиусу основания конической колбы, то высота, на которой будет находиться вода в цилиндрическом сосуде, будет равна 4 см.

и параллельные основания. Найдите объем их общей части, если объем

каждого конуса равен 8.

Задача №1 (группа 2)
Из двух одинаковых деревянных брусков объёмом 3куб.м, имеющих форму цилиндра, выточили конус (рис.1) и два конуса (рис.2). В каком случае будет сточено меньше материала?

рис.1

рис.2

РЕШИТЕ ЗАДАЧИ

«Авиационная бомба»
Авиационная бомба среднего калибра дает при

взрыве воронку диаметром 6 м и глубиной 2 м. Какое количество земли (по массе) выбрасывает эта бомба, если плотность земли 1650 кг /м3?

«Сено для коров»
У фермера 3 коровы. Для содержания одной коровы ему требуется заготовить на зиму 3 т сена. Он заготовил стог сена в виде конуса с радиусом основания 6 м и образующей 10 м. Определите массу заготовленного сена при плотности 30 кг/м3 .Хватит ли коровам сена на зиму?

земли по горсти в кучу.
И гордый холм возвысился,
И царь

мог с вышины
с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли.

А. С. Пушкин «Скупой рыцарь»

В биологии

«Конус выноса»
– форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину

ЭТО ИНТЕРЕСНО

«Конус нарастания»
–верхушка побега и корня
растений, состоящая из клеток образовательной
ткани.

«Конусами» называют семейство морских моллюсков подкласса
переднежаберных.

«Конус безопасности»- конус, образованный в пространстве около молниеотвода

«Телесный угол» -
конусообразный угол, вырезанный в шаре.

В науке и физике

же вы найдёте рецепт вафельных рожков с замороженным персиковым парфе)
3)Лукьяновой

К., Гаврюшиной Д. решить
задачу С2 (ЕГЭ).
4) Остальным учащимся решить №12,стр.129
5) Продолжить подготовку к ЕГЭ. Сайты для
оn-line тестирования http://math.reshuege.ru/
http://www.ege-online-test.ru/

Задача Определите объём наполнителя для вафельного рожка конической формы, диаметр основания которого 6 см, а образующая 15 см. Сколько литров наполнителя потребуется для приготовления 20 таких рожков?

вписанного в него шара. Найдите объём конуса, если образующая конуса

равна 10.

O

S

О1

Р

Р1

Решение.

1) Обозначим радиус шара r, а радиус основания конуса R.

2) По условию

т.е.

3) Δ SP1O1∞ΔSOP (∠Р1=∠О=90°, ∠S – общий),

откуда SO1 = 5.

5

5) Тогда

Коэффициент подобия треугольников k = ½.

R=2r

значит, r = 3, R=6

4) РР1= 2r, SP1= 10 – 2r, SO = 5+r.

Ответ: 96π.

6)Vк = ⅓πR²н

Vк=96π