Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия египетских пирамид
Содержание
- 1. Геометрия египетских пирамид
- 2. ВведениеОбъект изучения: Египетские пирамиды.Предмет изучения: геометрические особенности
- 3. Основные понятияПирамидой называется многогранник, который состоит из
- 4. РазмерыВысота 137,3 мСторона основания 233 мОбщий объем
- 5. Форма пирамид Правильные пирамиды – достаточно редкое
- 6. Форма пирамидНаклонные пирамидыЕдинственная в мире пирамида такого
- 7. Золотое сечениеЗолотое сечение, или золотая пропорция –
- 8. Золотое сечениеИсходным элементом, определяющим главные пропорции пирамиды,
- 9. Число πВ древнеегипетских мерах длина стороны квадрата,
- 10. Заключение Данная презентация посвящена выявлению основных
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Введение
Объект изучения: Египетские пирамиды.
Предмет изучения: геометрические особенности египетских пирамид.
Цель: изучить
историю построения и выявить геометрические особенности.
геометрические особенности пирамиды ХеопсаСлайд 3Основные понятия
Пирамидой называется многогранник, который состоит из плоского многоугольника –
основания пирамиды, точки, не лежащий в плоскости основания – вершины
пирамиды, и всех отрезков, соединяющих вершину с точками основания.Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Поверхность пирамиды состоит из основания и боковых граней.
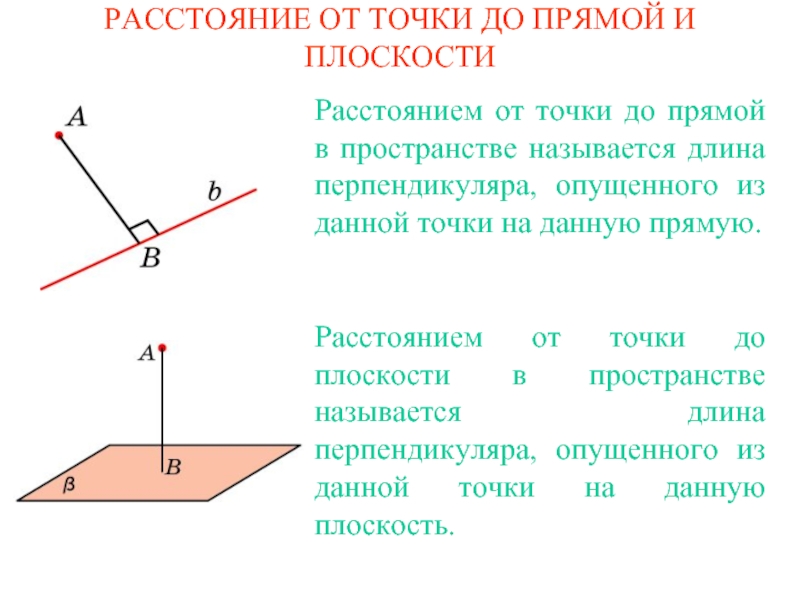
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Слайд 4Размеры
Высота 137,3 м
Сторона основания 233 м
Общий объем 2250000 куб.м
Площадь 54000
м2
На строительство пирамиды пошло около 2300000 каменных блоков, объема
свыше 1 куб.м. и веса 2,5 тонн каждый.Вес сооружения 6400000 тонн
В настоящие время, для того чтобы перевезти все камни, из которых сложена пирамида Хеопса, понадобилось бы 20 тысяч товарных поездов, по 30 вагонов каждый.
Слайд 5Форма пирамид
Правильные пирамиды – достаточно редкое явление. Обычно считается,
что у нее квадратное основание и четыре треугольные грани с
общей вершиной. Практически все египетские пирамиды этого типа имеют угол на клона боковых граней в 52°. Это единственный угол, обеспечивающий соотношение периметра основания и высоты пирамиды, равное 2*Pi.Большинство разбросанных по миру пирамид вздымается ввысь ступенями. Далеко не у всех ступенчатых пирамид квадратное основание. Многие пирамиды, в частности, Храм надписей в Паленке, имеют в своей основе прямоугольник. У пирамид майя часто почти отвесные боковые поверхности (порядка 70° ).
Слайд 6Форма пирамид
Наклонные пирамиды
Единственная в мире пирамида такого рода – пирамида
Снофру. Когда во время строительства высота пирамиды достигла более половины
от намеченной, наклон граней по отношению к основанию был резко изменен и уменьшился с 54 до 43°, что придало пирамиде ее «притуплённый» вид.Пирамиды конической формы
Самой крупной из известных конических пирамид считается холм Силбери-Хилл, расположенный в английском графстве Уилтшир. Холм поднимается на высоту 37,5 м, занимает площадь в 5 акров и возведен из более чем миллиона тонн уложенных вручную природных камней и грунта.
Слайд 7Золотое сечение
Золотое сечение, или золотая пропорция – деление отрезка таким
образом, чтобы отношение всего отрезка к его большей части равнялось
отношению большей части к меньшей.Слайд 8Золотое сечение
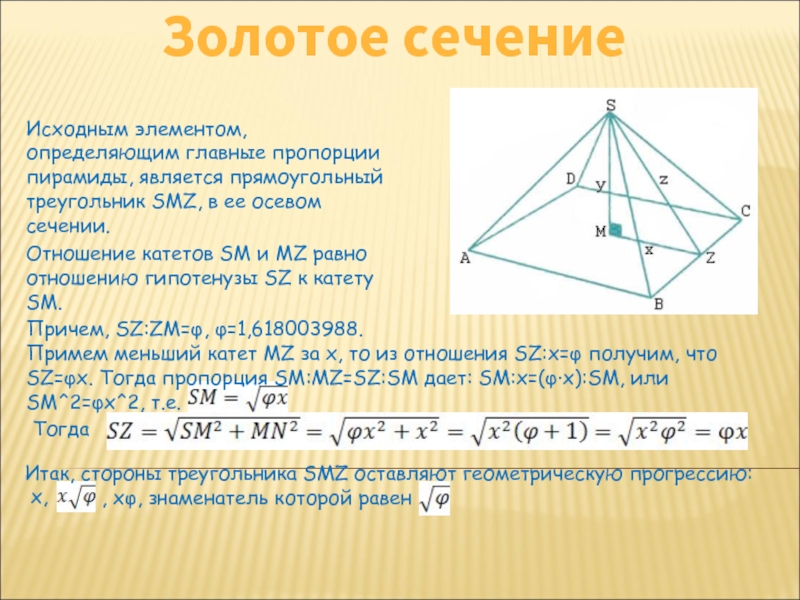
Исходным элементом, определяющим главные пропорции пирамиды, является прямоугольный треугольник
SMZ, в ее осевом сечении.
Отношение катетов SM и MZ
равно отношению гипотенузы SZ к катету SM.Причем, SZ:ZM=φ, φ=1,618003988.
Примем меньший катет MZ за х, то из отношения SZ:x=φ получим, что SZ=φx. Тогда пропорция SM:MZ=SZ:SM дает: SM:x=(φ·x):SM, или SM^2=φx^2, т.е.
Тогда
Итак, стороны треугольника SMZ оставляют геометрическую прогрессию:
x,
, xφ, знаменатель которой равен
.
Слайд 9Число π
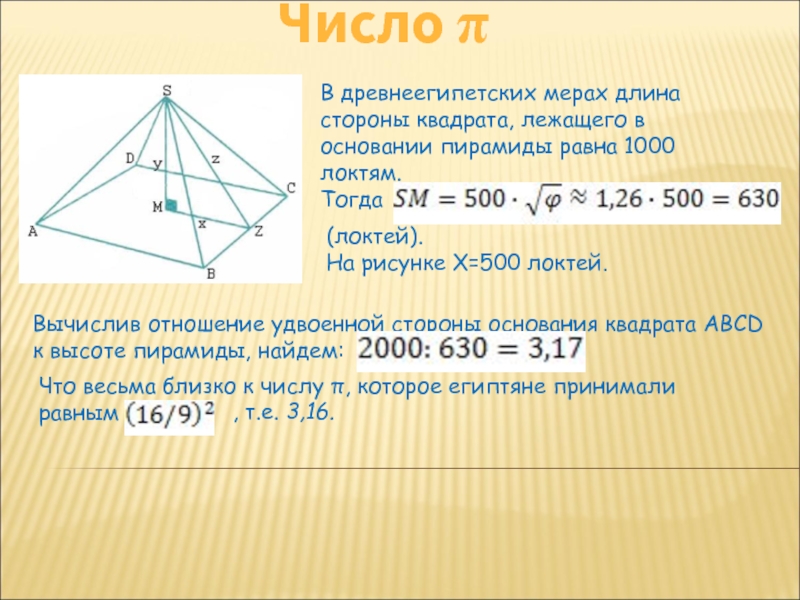
В древнеегипетских мерах длина стороны квадрата, лежащего в основании
пирамиды равна 1000 локтям.
Тогда
(локтей).
На рисунке X=500 локтей.
Вычислив отношение удвоенной
стороны основания квадрата ABCD к высоте пирамиды, найдем:Что весьма близко к числу π, которое египтяне принимали равным
, т.е. 3,16.
Слайд 10Заключение
Данная презентация посвящена выявлению основных геометрических особенностей египетских
пирамид.
Входе изучения были рассмотрены и описаны 4 варианта формы пирамид.
Также
при изучении были найдены следующие особенности:- наличие в размерах пирамиды золотого сечения;
- отношение удвоенной стороны, лежащего в основании пирамиды, к высоте пирамиды – есть число, очень близкое по значению к числу π.