Слайд 1Вступление
Человек немыслим без такого качества, как восприятие мира в его
красоте и гармонии. Поэтому сегодня одним из основных направлений развития
школы является поворот обучения к человеку, его ценностному потенциалу.
Известно, что решение задачи – одно из основных средств математического развития школьников. Каждая математическая задача служит конкретным целям обучения, но основная её цель – развитие творческого и математического мышления, формирование и развитие эстетического вкуса.
Слайд 2Вступление
Многие планиметрические задачи напрямую связаны с понятием "красивая", то есть
"доставляющая наслаждение, приятная внешним видом, гармоничностью, стройностью".
Решение "красивых" задач
должно быть наглядно, неожиданно, просто. Задачи, удовлетворяющие такому требованию неизменно вызывают интерес и побуждают к поиску более коротких и простых путей решения, что способствует развитию креативности.
Слайд 3Вступление
«Красота» задачи по решению проявляется в методах решения. Особый интерес
в этом смысле представляют задачи, имеющие несколько различных методов решения.
При решении планиметрических задач редко используют метод, основанный на применении описанной окружности. Я покажу на примерах «красоту решения» именно с использованием этого метода.
Слайд 4Свойство медианы прямоугольного треугольника
В учебнике «Геометрия 7-9» много вопросов вызывает
задача № 231: медиана АМ треугольника АВС равна половине стороны
ВС. Докажите, что треугольник АВС прямоугольный.
Существует несколько способов доказательства этого утверждения. На мой взгляд , применение описанной окружности – один из самых красивых способов решения.
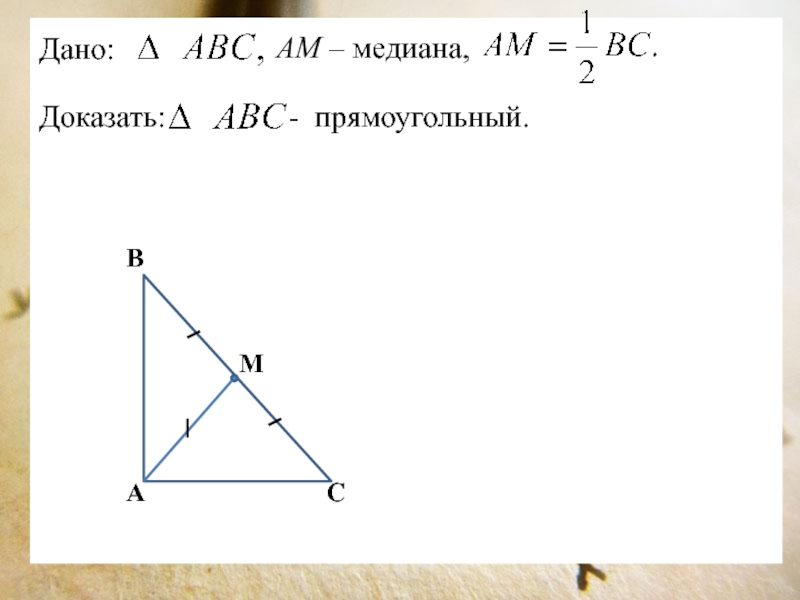
Слайд 5Дано:
Доказать:
- прямоугольный.
А
С
В
М
АМ – медиана,
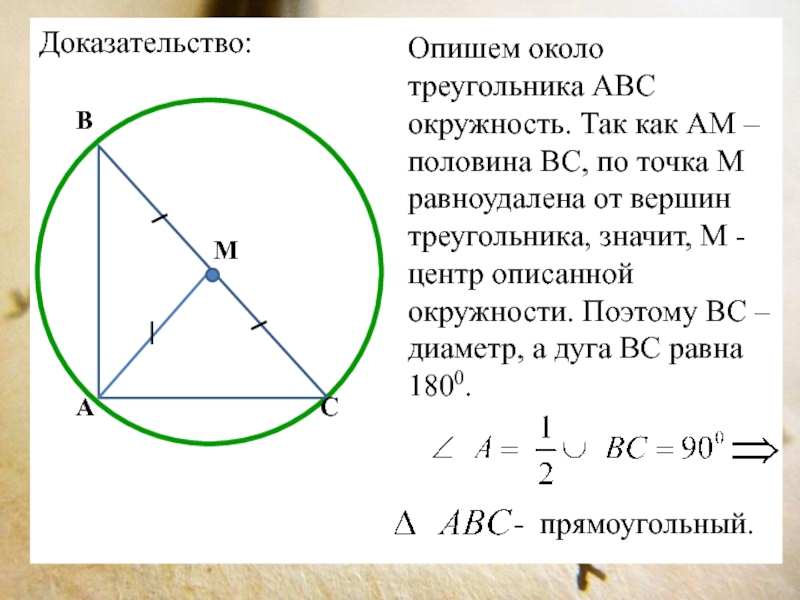
Слайд 6Доказательство:
Опишем около треугольника АВС окружность. Так как АМ – половина
ВС, по точка М равноудалена от вершин треугольника, значит, М
- центр описанной окружности. Поэтому ВС – диаметр, а дуга ВС равна 1800.
- прямоугольный.
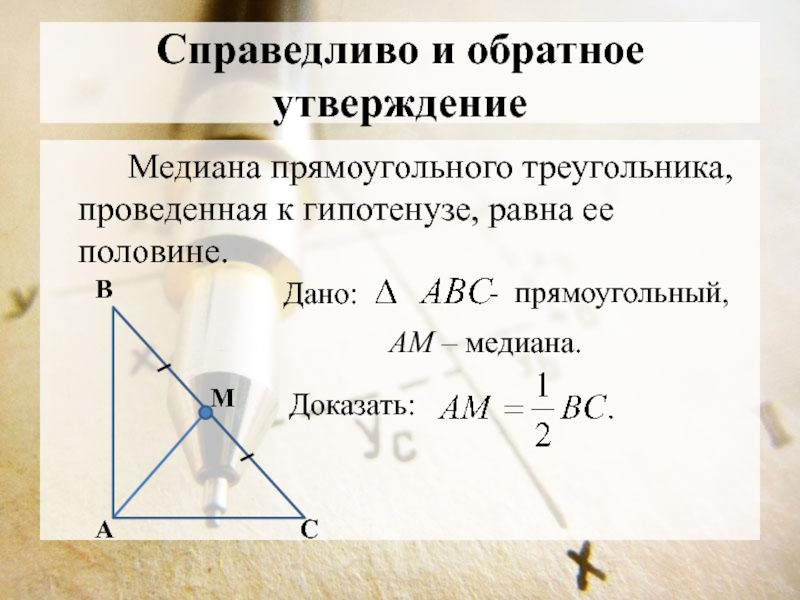
Слайд 7Справедливо и обратное утверждение
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна
ее половине.
Дано:
- прямоугольный,
АМ – медиана.
Доказать:
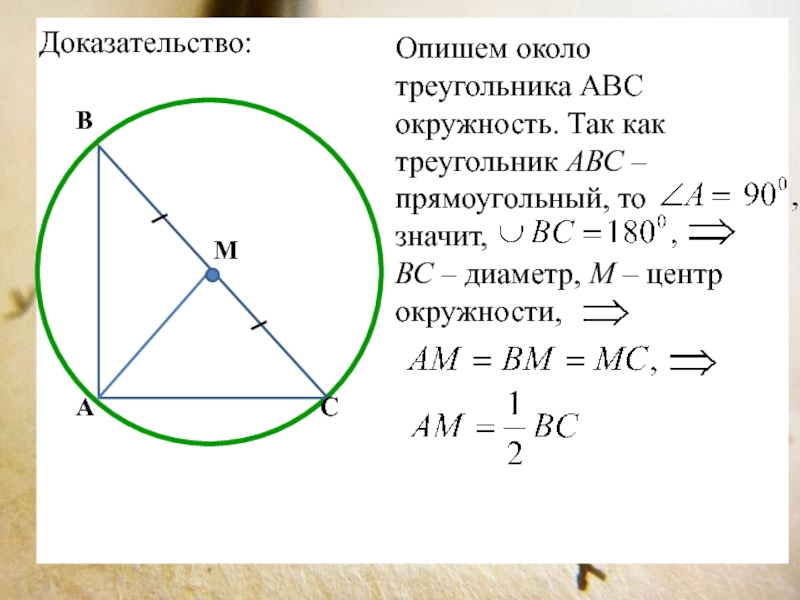
Слайд 8Доказательство:
А
С
В
М
Опишем около треугольника АВС окружность. Так как треугольник АВС –
прямоугольный, то значит,
ВС – диаметр,
М – центр окружности,
Слайд 9Применение окружности для решения задач ОГЭ по математике
ОГЭ 2017,
вариант 3 № 25.
В остроугольном треугольнике АВС проведены высоты ВВ1
и СС1. Докажите, что углы ВВ1С1 и ВСС1 равны.
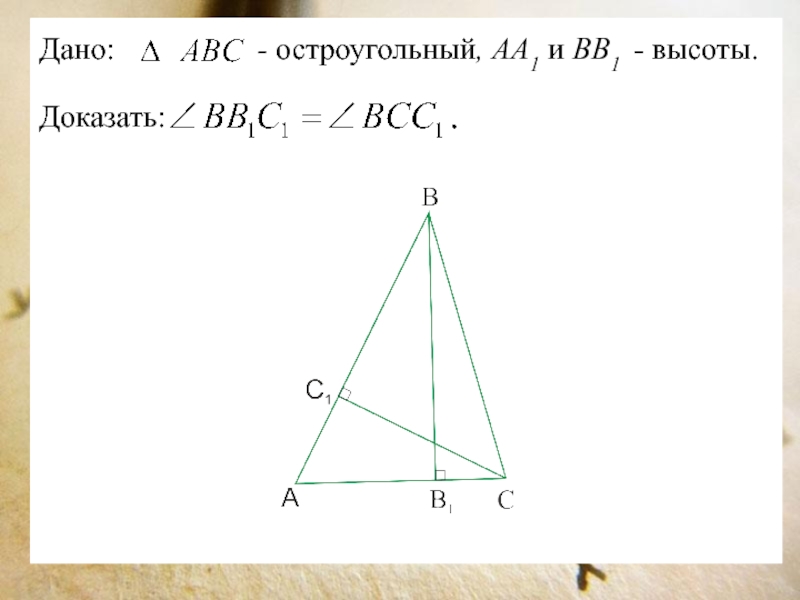
Слайд 10Дано:
Доказать:
- остроугольный, АА1 и ВВ1 - высоты.
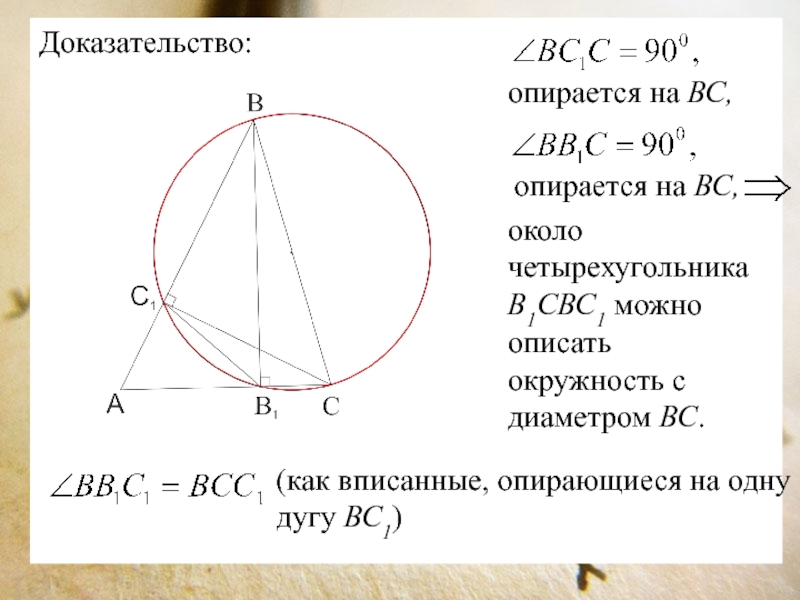
Слайд 11Доказательство:
опирается на ВС,
опирается на ВС,
около четырехугольника В1СВС1 можно описать
окружность с диаметром ВС.
(как вписанные, опирающиеся на одну дугу
ВС1)
Слайд 12Применение окружности для решения задач ОГЭ по математике
ОГЭ 2017,
вариант 21 № 25.
В треугольнике АВС с тупым углом АСВ
проведены высоты АА1 и ВВ1. Докажите, что треугольники А1СВ1 и АСВ подобны.
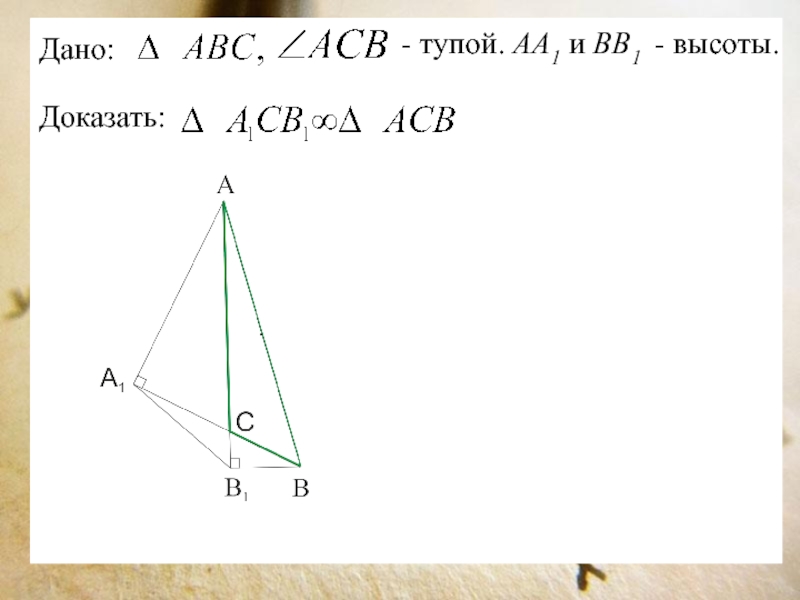
Слайд 13Дано:
Доказать:
- тупой. АА1 и ВВ1 - высоты.
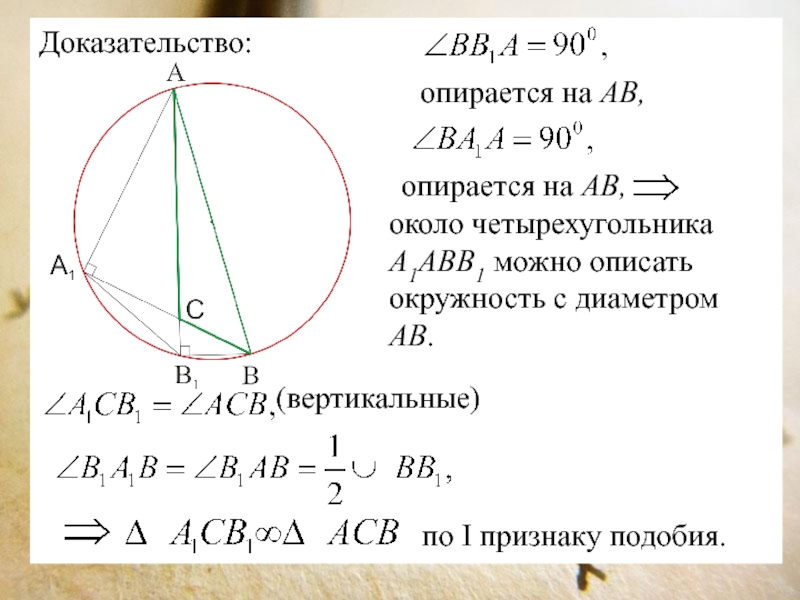
Слайд 14Доказательство:
опирается на АВ,
опирается на АВ,
около четырехугольника А1АВВ1 можно описать
окружность с диаметром АВ.
(вертикальные)
по I признаку подобия.
Слайд 15Свойство биссектрисы угла треугольника
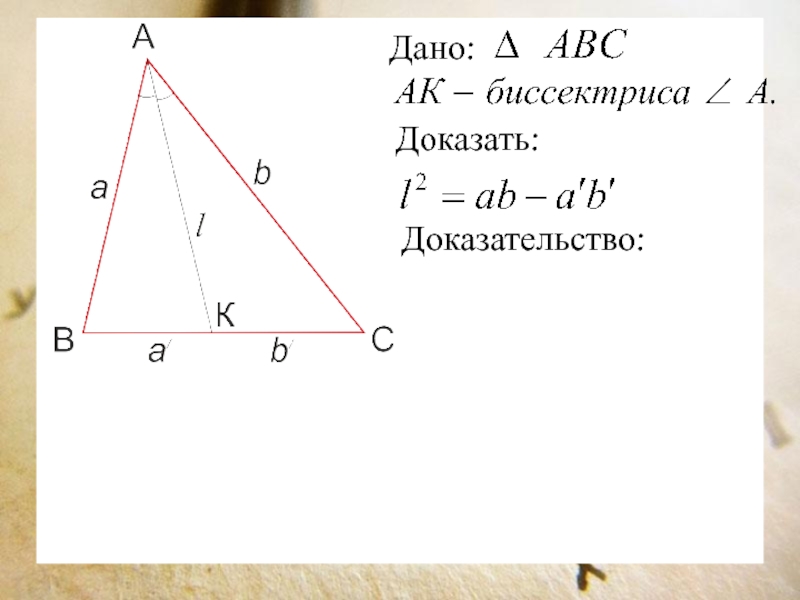
Доказать, что квадрат биссектрисы любого угла треугольника
равен разности произведений сторон треугольника, образующих избранный угол и отрезков,
на которые биссектриса делит третью сторону треугольника
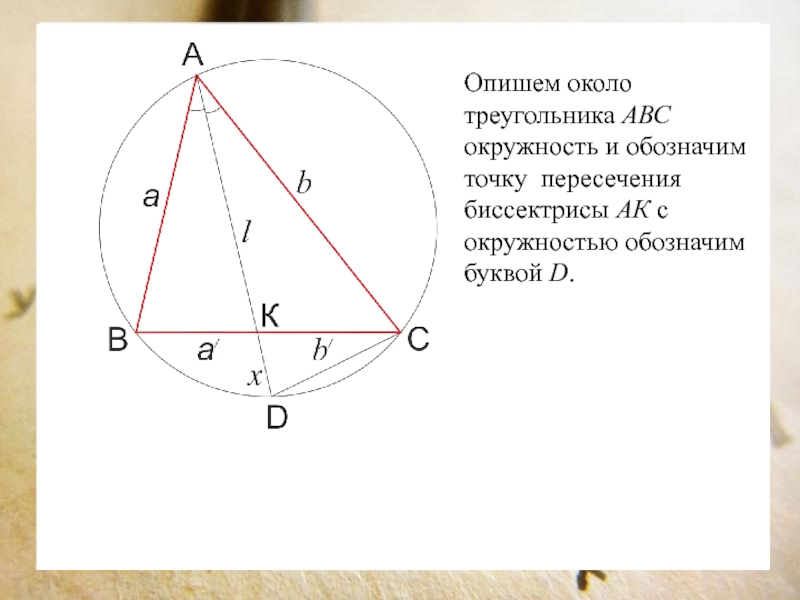
Слайд 17Опишем около треугольника АВС окружность и обозначим точку пересечения биссектрисы
АК с окружностью обозначим буквой D.
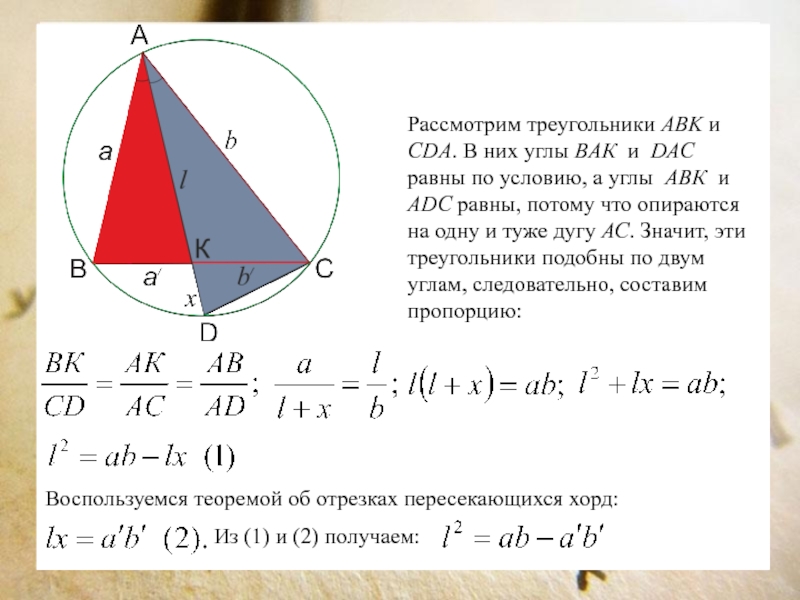
Слайд 18Рассмотрим треугольники ABK и CDA. В них углы BАК и
DАС равны по условию, а углы АВК и АDC равны,
потому что опираются на одну и туже дугу АС. Значит, эти треугольники подобны по двум углам, следовательно, составим пропорцию:
Воспользуемся теоремой об отрезках пересекающихся хорд:
Из (1) и (2) получаем:
Слайд 19 Доказанную задачу можно рассматривать как теорему. Формула для вычисления длины
биссектрисы угла треугольника часто используется при решении других задач.
В сборнике
задач по математике под редакцией М. И. Сканави я нашел пример задачи, при решении которой удобно применить полученную формулу:
№ 10. 368 Вычислить длину биссектрисы угла A треугольника ABC с длинами сторон а = 18 см, b = 15 см и c =12 см
Применение формулы
Слайд 20Дано:
Найти:
Решение: чтобы воспользоваться результатом доказанной теоремы, найдем отрезки
СК и BК. По теореме о биссектрисе угла треугольника имеем:
Ответ:
10 см.
Слайд 21Заключение
В данной работе рассмотрено решение планиметрических задач с помощью понятия
описанной окружности. Этот метод упрощает процесс решения, делает его наглядным,
простым, «красивым».
Слайд 22Источники информации
Шаблон презентации presen.ru
Изображения License Some rights reserved by zaveqna
Видеоресурсы « Красивые идеи красивых задач в школьной геометрии» Рафаил
Калманович Гордин https://www.youtube.com/watch?v=L0Po61NA65s
Слайд 23Источники информации
Литература:
ОГЭ. Математика: типовые экзаменационные варианты: 36 вариантов/ под ред.
И. В. Ященко. – М.: Издательство «Национальное образование». 2017
Геометрия, 7-9:
Учеб. Для общеобразоват. учреждений/ Л. С. Атанасян. В. Ф. Бутузов. С. Б. Кадомцев и др.- М.: Просвещение, 2009
Сборник задач по математике для поступающих во втузы под редакцией М. И. Сканави. – М.: ООО «Издательство «Мир и образование»: ООО «Издательство «ОНИКС – ЛИТ», 2013