Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История развития геометрии по Лобачевскому
Содержание
- 1. История развития геометрии по Лобачевскому
- 2. Титульный лист книги Лобачевского «Воображаемая геометрия», 1835
- 3. Геометрия Лобачевского – это интересный, необычный раздел
- 4. В развитии геометрии можно указать четыре
- 5. Первый – период зарождения геометрииПервый – период
- 6. Второй период развития геометрииВторой период развития геометрии
- 7. Третий период выделяют с 1-й половины XVII
- 8. Четвертый период в развитии геометрии открывается построением
- 9. История создания геометрии Лобачевского одновременно является историей
- 10. 23 февраля 1826 г. российский математик Николай
- 11. «Треугольник» по Лобачевскому, у которого сумма углов
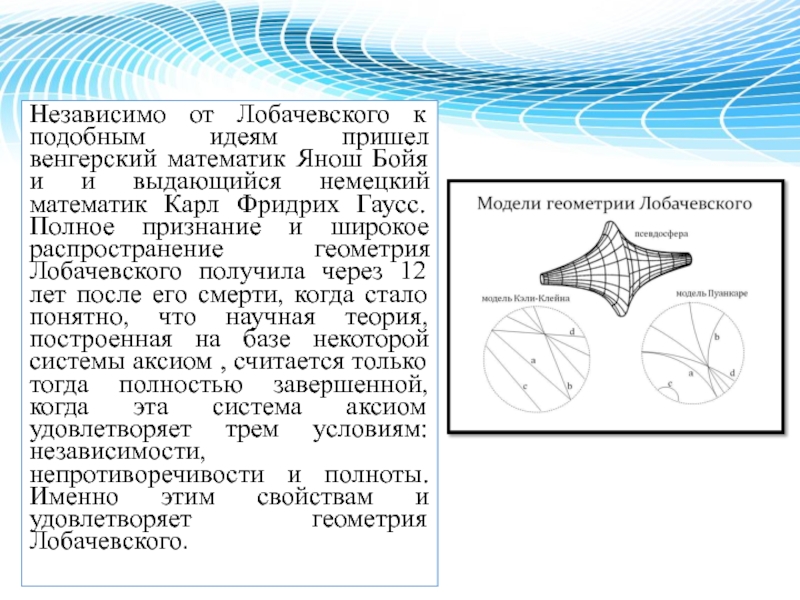
- 12. Независимо от Лобачевского к подобным идеям пришел
- 13. Использованная литература1. Каган В. Ф. Лобачевский и
- 14. Скачать презентанцию
Титульный лист книги Лобачевского «Воображаемая геометрия», 1835 г.Лобачевскому было всего 34 года, когда он решил «многовековую» проблему пятого постулата из «Начал» Евклида и построил свою, неевклидову геометрию. Николай Иванович Лобачевский решил
Слайды и текст этой презентации
Слайд 3
Геометрия Лобачевского – это интересный, необычный раздел современной геометрии. Она
дает материал для размышлений – в ней не всё так
просто, не всё так ясно с первого взгляда. Чтобы ее понять, нужно обладать фантазией и пространственным воображением.Николай Иванович Лобачевский
(1792-1856 гг.)
великий русский математик
Слайд 4 В развитии геометрии можно указать четыре основных периода, переходы между
которыми обозначали качественное изменение этой науки:
Первый период зарождения геометрии.
Второй период
развития геометрии. Третий период связан он с введением в геометрию метода координат.
Четвертый период -построение новой, неевклидовой геометрии-геометрией Лобачевского.
Слайд 5Первый – период зарождения геометрии
Первый – период зарождения геометрии как
математической науки протекал в Древнем Египте, Вавилоне и Греции примерно
до V в. до н. э. Зачатками науки следует считать установление первых общих закономерностей, в данном случае – зависимостей между геометрическими величинами.Слайд 6Второй период развития геометрии
Второй период развития геометрии связан с ее
становлением как самостоятельной математической науки: появились систематические изложения, где ее
предложения последовательно доказывались. Примерно в 300 г. до н. э. свет увидел труд, ставший основой всей современной геометрии, – «Начала» Евклида. В «Началах» собраны все геометрические сведения, полученные трудами десятков математиков античности, живших до Евклида. Этот труд, состоящий из тридцати больших томов, на два тысячелетия стал единственным учебником, по которому можно было изучить геометрию. И «Начала» прекрасно описывают пространство, в котором мы живем, благодаря чему эту геометрию назвали геометрией Евклида.Слайд 7Третий период выделяют с 1-й половины XVII в., и связан
он с Рене Декартом, который ввел в геометрию метод координат.
Этот метод позволил связать геометрию с развивавшейся тогда алгеброй и зарождающимся анализом. Применение методов этих наук в геометрии породило аналитическую геометрию, а потом и дифференциальную.Третий период развития геометрии
Слайд 8Четвертый период в развитии геометрии открывается построением Н. И. Лобачевским
в 1826 г. новой, неевклидовой геометрии, называемой теперь геометрией Лобачевского.
Четвертый период развития геометрии
Слайд 9История создания геометрии Лобачевского одновременно является историей попыток доказать пятый
постулат Евклида. Этот постулат представляет собой одну из аксиом, положенных
Евклидом в основу изложения геометрии. На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам евклидовой. Из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. Все теоремы, не зависящие от этого пятого постулата, являются общими для обеих геометрий. они образуют так называемую абсолютную геометрию. Напомним формулировку этого пятого постулата: если две прямые пересекаются третьей так, что по какую-либо сторону от нее сумма внутренних углов меньше двух прямых углов, то по эту же сторону исходные прямые пересекаются. Звучит его формулировка чрезвычайно сложно, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.Слайд 1023 февраля 1826 г. российский математик Николай Иванович Лобачевский на
заседании физико-математического факультета Казанского университета провозгласил о создании новой геометрии,
названной им «воображаемой геометрией». Геометрия была основана на тех же традиционных постулатах и аксиомах геометрии, как и у Евклида, но с заменой его пятого постулата о параллельных.Слайд 11«Треугольник» по Лобачевскому, у которого сумма углов менее 180°
В
геометрии Лобачевского пространство не плоско, оно имеет некоторую отрицательную кривизну.
Представить это достаточно сложно, но хорошей моделью такого пространства являются геометрические тела, похожие на воронку и седло. Геометрия Лобачевского на первый взгляд не согласуется с нашими привычными представлениями о геометрии пространства. Например, в геометрии Лобачевского сумма углов у каждого треугольника своя и всегда меньше 180 градусов.Слайд 12Независимо от Лобачевского к подобным идеям пришел венгерский математик Янош
Бойя и и выдающийся немецкий математик Карл Фридрих Гаусс. Полное
признание и широкое распространение геометрия Лобачевского получила через 12 лет после его смерти, когда стало понятно, что научная теория, построенная на базе некоторой системы аксиом , считается только тогда полностью завершенной, когда эта система аксиом удовлетворяет трем условиям: независимости, непротиворечивости и полноты. Именно этим свойствам и удовлетворяет геометрия Лобачевского.Слайд 13Использованная литература
1. Каган В. Ф. Лобачевский и его геометрия: общедоступные
очерки. – М.: Государственное издательство технико теоретической литературы, 1955. –
305 с.2. Широков П. А. Краткий очерк основ геометрии Лобачевского: учеб. пособие. – М.: Государственное издательство технико-теоретической литературы, 1955. – 80 с.
3. Атанасян Л. С. Геометрия Лобачевского. – М.: Просвещение, 2001. – 336 с.
4. Атанасян Л. С. Геометрия Лобачевского: учеб. электронное издание. – М.: БИНОМ. Лаборатория знаний, 2014. – 464 с.
5. Атанасян Л. С. Геометрия Лобачевского. – М.: Просвещение, 2001. – 336 с.
6. Атанасян Л. С. Геометрия Лобачевского. – М.: БИНОМ. Лаборатория знаний, 2014. – 464 с.