Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многоугольники
Содержание
- 1. Правильные многоугольники
- 2. Правильные многоугольникиНа этом уроке вы узнаете, как
- 3. Слайд 3
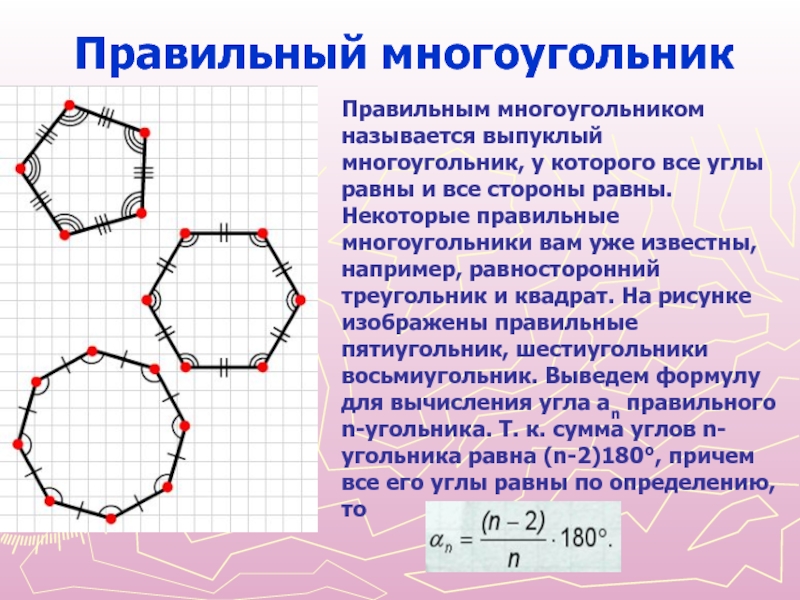
- 4. Правильным многоугольником называется выпуклый многоугольник, у которого
- 5. Центр правильного многоугольника Центром
- 6. В каждом правильном многоугольнике есть точка, равноудаленная
- 7. Слайд 7
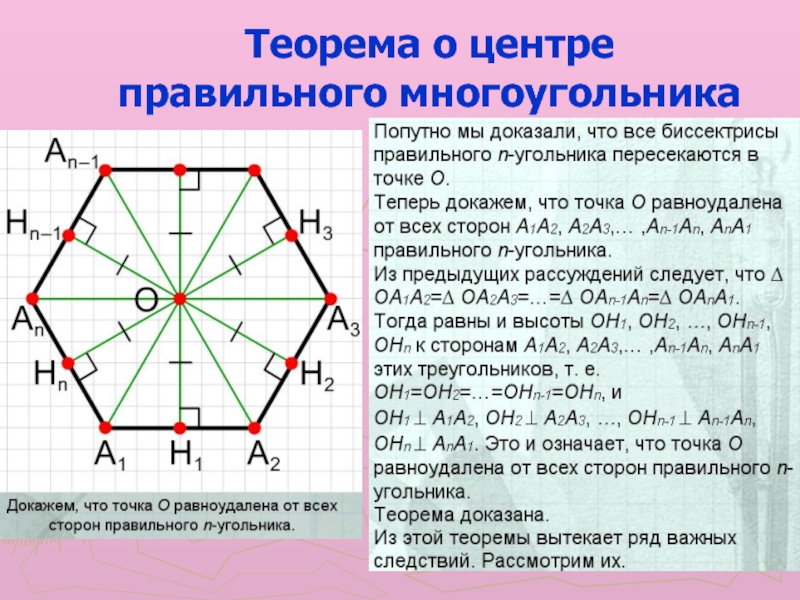
- 8. Теорема о центре правильного многоугольника
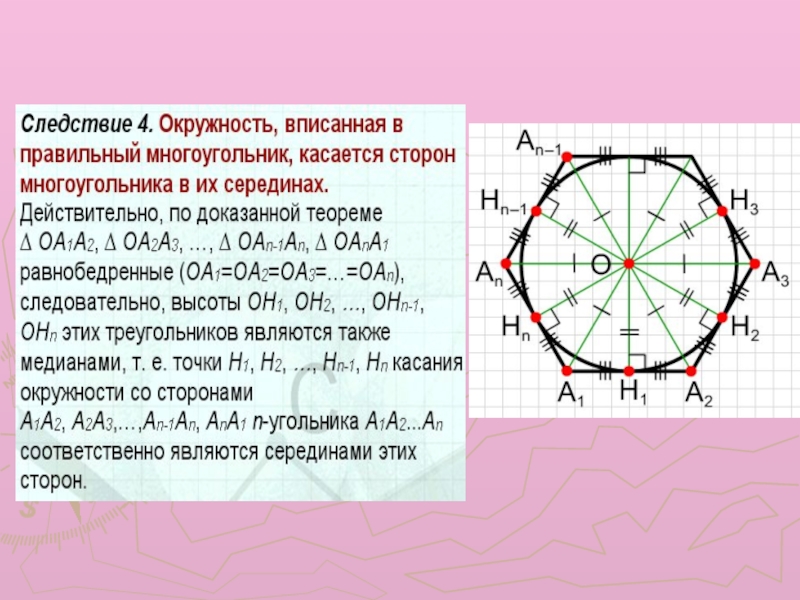
- 9. Следствие 1. Около любого правильного многоугольника можно
- 10. Слайд 10
- 11. Докажем теперь единственность такой окружности. Предположим, что,
- 12. Слайд 12
- 13. Центр окружности, описанной около правильногомногоугольника, совпадает с
- 14. Слайд 14
- 15. Выводы
- 16. Автор: Аверкина Т.П., учитель МОУ «Тархановская СОШ» Ичалковского района РМ
- 17. Скачать презентанцию
Правильные многоугольникиНа этом уроке вы узнаете, как называется выпуклый многоугольник, у которого все углы и все стороны равны; познакомитесь с выводом формулы для вычисления угла правильного n-угольника, а также сможете провести
Слайды и текст этой презентации
Слайд 2Правильные многоугольники
На этом уроке вы узнаете, как называется выпуклый многоугольник,
у которого все углы и все стороны равны;
выводом формулы для вычисления угла правильного n-угольника, а также сможете провести доказательство теоремы о центре правильного многоугольника и рассмотрите ряд полезных следствий из этой теоремы.Слайд 4Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны
и все стороны равны. Некоторые правильные многоугольники вам уже известны,
например, равносторонний треугольник и квадрат. На рисунке изображены правильные пятиугольник, шестиугольники восьмиугольник. Выведем формулу для вычисления угла аn правильного n-угольника. Т. к. сумма углов n-угольника равна (n-2)180°, причем все его углы равны по определению, тоПравильный многоугольник
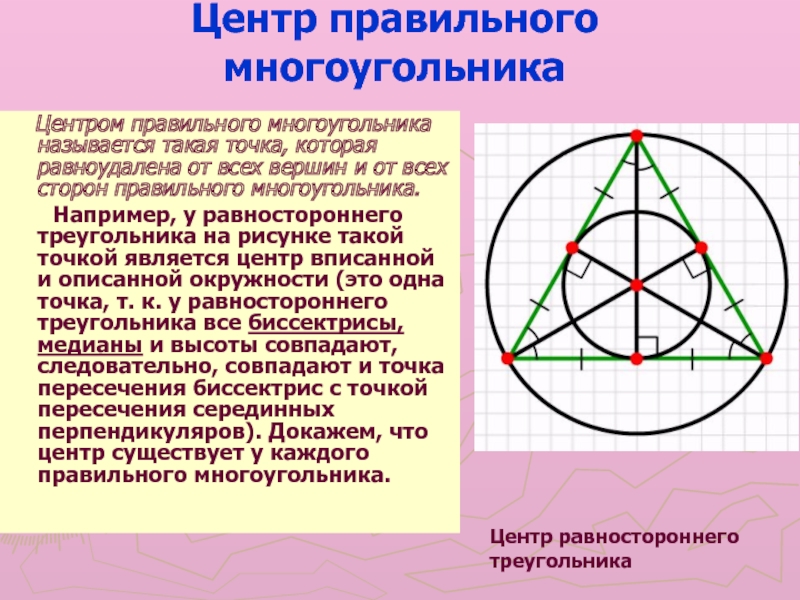
Слайд 5Центр правильного многоугольника
Центром правильного многоугольника называется такая
точка, которая равноудалена от всех вершин и от всех сторон
правильного многоугольника.Например, у равностороннего треугольника на рисунке такой точкой является центр вписанной и описанной окружности (это одна точка, т. к. у равностороннего треугольника все биссектрисы, медианы и высоты совпадают, следовательно, совпадают и точка пересечения биссектрис с точкой пересечения серединных перпендикуляров). Докажем, что центр существует у каждого правильного многоугольника.
Центр равностороннего
треугольника
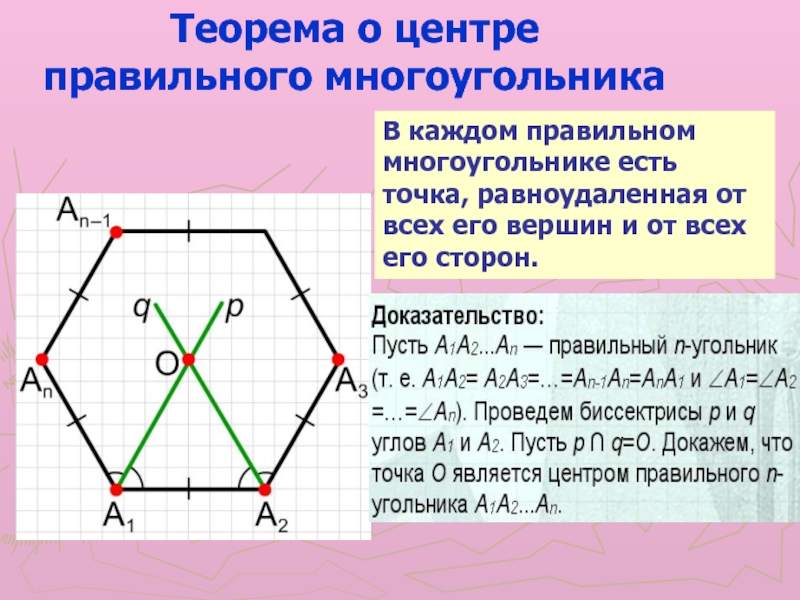
Слайд 6В каждом правильном многоугольнике есть точка, равноудаленная от всех его
вершин и от всех его сторон.
Теорема о центре
правильного
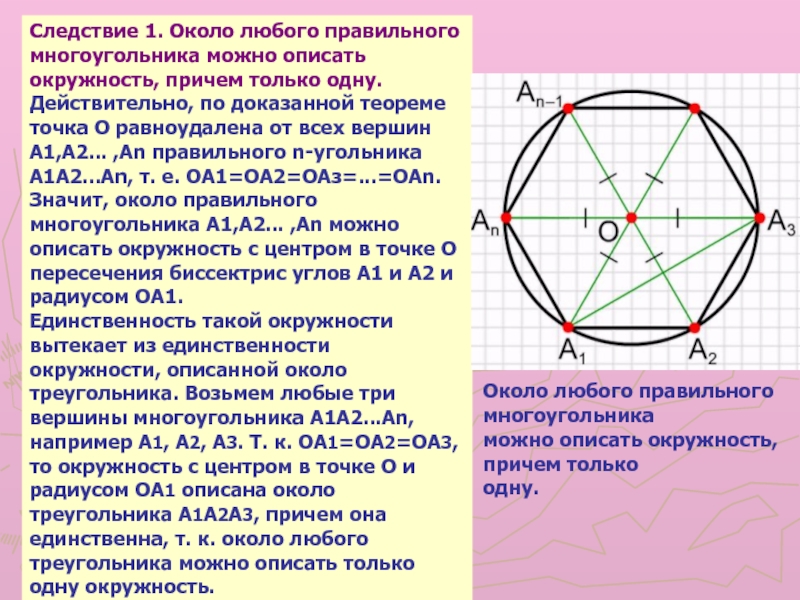
многоугольникаСлайд 9Следствие 1. Около любого правильного многоугольника можно описать окружность, причем
только одну.
Действительно, по доказанной теореме точка О равноудалена от всех
вершин A1,A2... ,An правильного n-угольника A1A2...An, т. е. ОА1=ОА2=ОАз=...=ОАn. Значит, около правильного многоугольника A1,A2... ,An можно описать окружность с центром в точке О пересечения биссектрис углов A1 и А2 и радиусом OA1.Единственность такой окружности вытекает из единственности окружности, описанной около треугольника. Возьмем любые три вершины многоугольника A1A2...An, например A1, A2, А3. Т. к. ОА1=ОА2=ОА3, то окружность с центром в точке О и радиусом OA1 описана около треугольника A1A2A3, причем она единственна, т. к. около любого треугольника можно описать только одну окружность.
Около любого правильного многоугольника
можно описать окружность, причем только
одну.
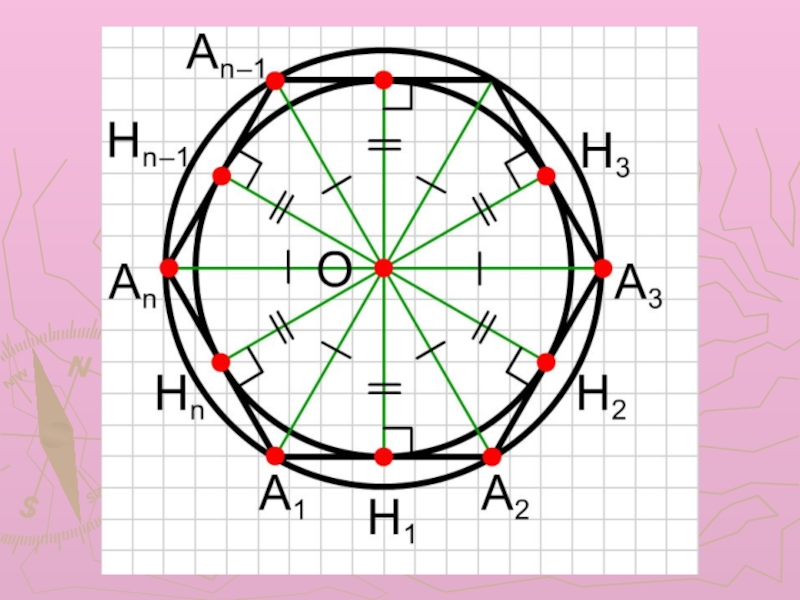
Слайд 11Докажем теперь единственность такой окружности. Предположим, что, кроме указанной окружности
с центром O и радиусом ОН1, существуют еще одна вписанная
в n-угольник А1A2..Аn окружность с центром в точке O1, отличной от O. Но тогда ее центр O1 равноудален от сторон многоугольника, т. е. точка O1 лежит на каждой из биссектрис углов многоугольника, следовательно, совпадает с точкой O пересечения этих биссектрис. Кроме того, т. к. из одной точки O на каждую сторону n-угольника можно опустить только один перпендикуляр, то и радиус второй окружности совпадает с ОН1. Значит, вписанная в правильный многоугольник окружность только одна.Следствия из теоремы
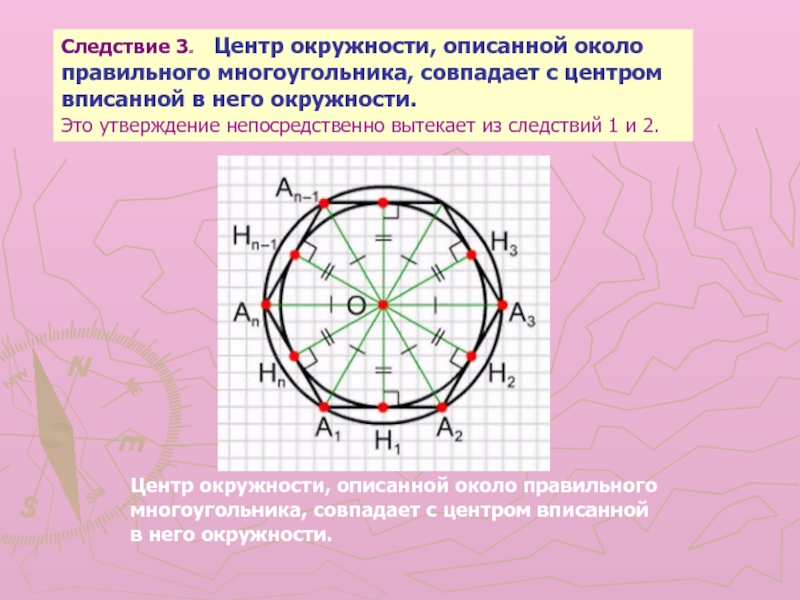
Слайд 13Центр окружности, описанной около правильного
многоугольника, совпадает с центром вписанной
в него
окружности.
Следствие 3. Центр окружности, описанной около правильного многоугольника,
совпадает с центром вписанной в него окружности. Это утверждение непосредственно вытекает из следствий 1 и 2.