Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Доклад о «Сфере и шаре»
Содержание
- 1. Доклад о «Сфере и шаре»
- 2. Все о сфереВсе о шареЧто такое Сферическая геометрия?Что такое сферическая тригонометрия?План презентации:
- 3. Сфера-это множество точек трехмерного евклидова пространства, находящихся
- 4. Шар – это тело, происходящее от вращения
- 5. Всякое сечение шара плоскостью есть круг
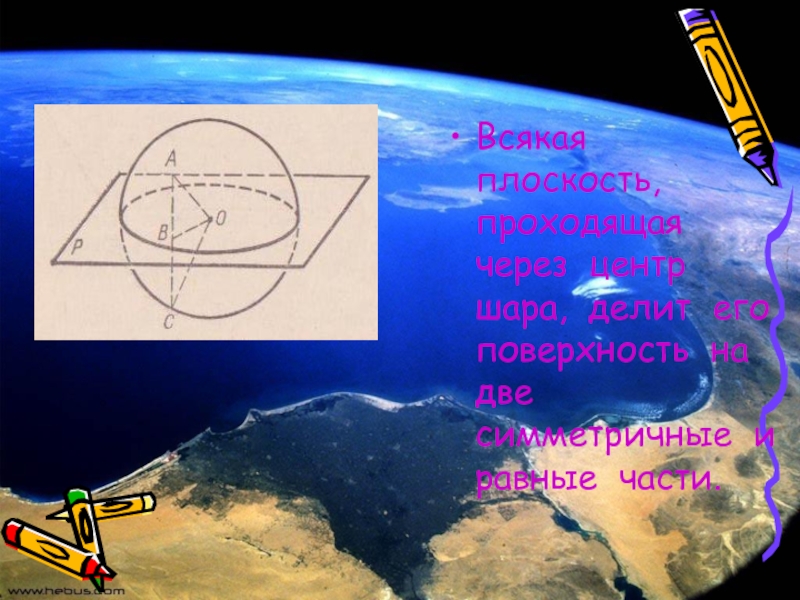
- 6. Всякая плоскость, проходящая через центр шара, делит его поверхность на две симметричные и равные части.
- 7. Через две точки шаровой поверхности, не лежащие
- 8. Часть шаровой поверхности отсекаемая от нее какой-нибудь
- 9. Сферическая геометрия – это геометрическая дисциплина, изучающая
- 10. Сферическая тригонометрия – это тригонометрия сферического треугольника,
- 11. Скачать презентанцию
Все о сфереВсе о шареЧто такое Сферическая геометрия?Что такое сферическая тригонометрия?План презентации:
Слайды и текст этой презентации
Слайд 1Доклад о «Сфере и шаре»
Работу выполнила ученица
11 класса Дерябина Юлия Учитель: Хайбрахманова Г.Ф.
Слайд 2Все о сфере
Все о шаре
Что такое Сферическая геометрия?
Что такое сферическая
тригонометрия?
План презентации:
Слайд 3Сфера-это множество точек трехмерного евклидова пространства, находящихся на данном положительном
расстоянии от данной точки. Данная точка называется центром сферы. Если
О – данная точка, а М – любая точка сферы ., то отрезок ОМ, как и расстояние |ОМ|, называется радиусом сферы. Чаще всего радиус сферы. Обозначается буквами r или R. сферы с центром О и радиусом Rобозначается так: (О;R) или S². Отрезок (или его длинна), соединяющий две точки сферы., называется её хордой. Хорда, проходящая через центр, называется диаметром сферы. Длинна диаметра d = 2R. Сечение сферы плоскостью, находящийся от центра сферы. На расстоянии, меньше радиуса, есть окружность. Уравнение сферы в прямоугольной декартовой системе координат имеет вид:
( х – а)² + ( у – b)² + ( z – c)² = R²,
где, a,b,c – координаты центра, а R – радиус сферы. Сферу можно рассматривать как поверхность, полученную от вращения окружности вокруг своего диаметра. Площадь поверхности сфера радиуса R находится как производная объема шара по радиусу:
S = 4πR²
Касательная плоскость к сфера перпендикулярна радиусу, проведенному в точку касания. Сферу обычно изображают в ортогональной проекции, так как абрис сферы есть окружность, а в произвольной параллельной проекции абрис сферы есть эллипс
Всё о сфере
Слайд 4Шар – это тело, происходящее от вращения полукруга вокруг диаметра,
ограничивающего его, а поверхность, образуемая при этом полуокружностью, называется шаровой
или сферической поверхностью. Еще одно определение шара: шар – это множество точек трехмерного евклидова пространства, расстояние от каждой из которых до данной точки не больше расстояния R. Данная точка называется центром шара, а расстояние R- радиусом его. Если центр шара совпадает с началом координат и радиус его равен R, то шар с центром О и радиус R можно определить как множество точек пространства, координаты которых удовлетворяют неравенствух² + у² + z² ≤R².
Шар можно определить как тело вращения полукруга вокруг оси, содержащий диаметр полукруга. Граничные точки шара образуют сферу с тем же центром и тем же радиусом. Всякое сечение шара плоскостью есть круг. Шар есть пространственный аналог круга. Объем шара равен : V = 4⁄3 πR³.
Шар имеет бесконечное множество осей и плоскостей симметрии и один центр.
Всё о "шаре"
Слайд 6Всякая плоскость, проходящая через центр шара, делит его поверхность на
две симметричные и равные части.
Слайд 7Через две точки шаровой поверхности, не лежащие на концах одного
диаметра, можно провести окружность большого круга и только одну
Слайд 8Часть шаровой поверхности отсекаемая от нее какой-нибудь плоскостью, называется сегментной
поверхностью.
Часть шаровой поверхности, заключенная между двумя параллельными секущими плоскостями, называется
шаровым поясом или зоной.Плоскость шара и его частей
Слайд 9Сферическая геометрия – это геометрическая дисциплина, изучающая свойства фигур, расположенных
на сфере. Сферическая геометрия изучает свойства фигур на плоскости. Большие
круги на сфере, являясь геодезическими линиями, играют роль прямых на плоскости: через две точки сферы, не совпадающие с концами ее диаметра, проходит только одна большая окружность сферической геометрии аналогично тому, как на плоскости через две различные точки проходит только одна прямая. Однако в сферической геометрии нельзя провести параллельных «прямых», в то время как на плоскости Евклида и плоскости Лобачевского существуют параллельные прямые. Основными фигурами сферической геометрии являются сферические двуугольники, сферические треугольники, сферические многоугольники, т.е многоугольники на сфере, сторонами которых являются дуги больших окружностей, длинна которых меньше длинны полуокружности. Сферу, как и плоскость, можно перемещать по самой себе. Сферическая геометрия одна из простейших геометрий, отличных от обычной геометрии Евклида. В этой геометрии много удивительных фактов, не имеющих места в геометрии Евклида. Сферическая геометрия находит применение в астрономии, в географии, в мореплавании и других науках и областях знаний.Что такое сферическая геометрия?
Слайд 10Сферическая тригонометрия – это тригонометрия сферического треугольника, т.е раздел математики,
изучающий зависимость между сторонами и углами сферического треугольника. В
отличие от плоской тригонометрии, в сферической тригонометрии три угла треугольника однозначно определяют его форму и размер. В сферической тригонометрии имеет место своя теорема косинусов и своя теорема синусов.Что такое сферическая тригонометрия?
Теги