Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на построение 7 класс
Содержание
- 1. Задачи на построение 7 класс
- 2. Цели: познакомить учащихся с задачами на построение
- 3. Из истории математикиВ 1672 г. Датский математик
- 4. Тест по теме «Окружность» Выберите правильный вариант
- 5. Тест по теме «Окружность» Выберите правильный вариант
- 6. Тест ( продолжение)3. Радиусом окружности называется
- 7. Тест(продолжение)5. Диаметром окружности называется а) прямая,
- 8. АВСПостроение угла, равного данному.Дано: угол А.ОDEТеперь докажем, что построенный угол равен данному.
- 9. Построение угла, равного данному.Дано: угол А.АПостроили угол
- 10. биссектрисаПостроение биссектрисы угла.
- 11. Докажем, что луч АВ – биссектриса
- 12. ВАПостроение перпендикулярных прямых.
- 13. Докажем, что а РМАМ=МВ, как радиусы
- 14. aNМПостроение перпендикулярных прямых.
- 15. aNBACМПосмотрим на расположение циркулей.АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам
- 16. Докажем, что О – середина отрезка АВ.Построение середины отрезка
- 17. ВАТреугольник АРВ р/б.Отрезок РО является биссектрисой, а
- 18. DСПостроение треугольника по двум сторонам и углу
- 19. DСПостроение треугольника по стороне и двум прилежащим
- 20. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
- 21. Подведение итогов урока Оцените свою работу, выбрав
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Задачи на построение
Это такие задачи, при
решении которых нужно построить
геометрическую
деленийСлайд 2Цели:
познакомить учащихся с задачами на построение
рассмотреть наиболее простые
задачи на построение и научить учащихся решать их.
формировать
умение решать простые задачи на построениерасширить знания об истории геометрии
воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при изучении темы
воспитание интереса к истории математики, как науки.
развитие навыков самоконтроля
формирование алгоритмического мышления
Слайд 3Из истории математики
В 1672 г. Датский математик Георг Мор, а
затем в 1797 г. итальянский учёный Лоренцо Маскерони доказали независимо
один от другого такое утверждение: всякая задача на построение, разрешимая с помощью циркуля и линейки, разрешима также с помощью одного только циркуля. Эти название построения носят построения Мора - Маскерони.Швейцарский геометр Якоб Штейнер в 1883 г., а несколько раньше французский математик Ж.Понселе доказали тоже независимо друг от друга такое утверждение: любая задача на построение, разрешимая с помощью циркуля и линейки, может быть разрешена с помощью линейки, если только в плоскости чертежа задана окружность и её центр. Такие построения носят название построения Понселе -Штейнера.
Слайд 4Тест по теме «Окружность»
Выберите правильный вариант ответа.
1. Окружностью называется геометрическая
фигура, которая
а) состоит из точек плоскости, расположенных
на данном расстоянии от данной точки плоскости;б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости.
2. Центром окружности является
а) точка, от которой одинаково удалены некоторые точки;
б) точка, от которой одинаково удалены все точки окружности.
Слайд 5Тест по теме «Окружность»
Выберите правильный вариант ответа.
1. Окружностью называется геометрическая
фигура, которая
а) состоит из точек плоскости, расположенных
на данном расстоянии от данной точки плоскости;б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости.
2. Центром окружности является
а) точка, от которой одинаково удалены некоторые точки;
б) точка, от которой одинаково удалены все точки окружности.
Слайд 6Тест ( продолжение)
3. Радиусом окружности называется
а) отрезок, соединяющий
любую точку окружности с центром;
б) отрезок, соединяющий любую
точку окружности с центром окружности.4. Хордой окружности называется
а) отрезок, соединяющий две любые точки окружности;
б) отрезок, соединяющий две любые точки.
Слайд 7Тест(продолжение)
5. Диаметром окружности называется
а) прямая, проходящая через центр
окружности;
б) хорда, проходящая через центр окружности.
Оцени себя.
Если у
тебя 5 верных ответов – оценка 5;4 верных ответа -- оценка 4;
3 верных ответа -- оценка 3.
Меньшее число верных ответов оценивается 2.
Слайд 8А
В
С
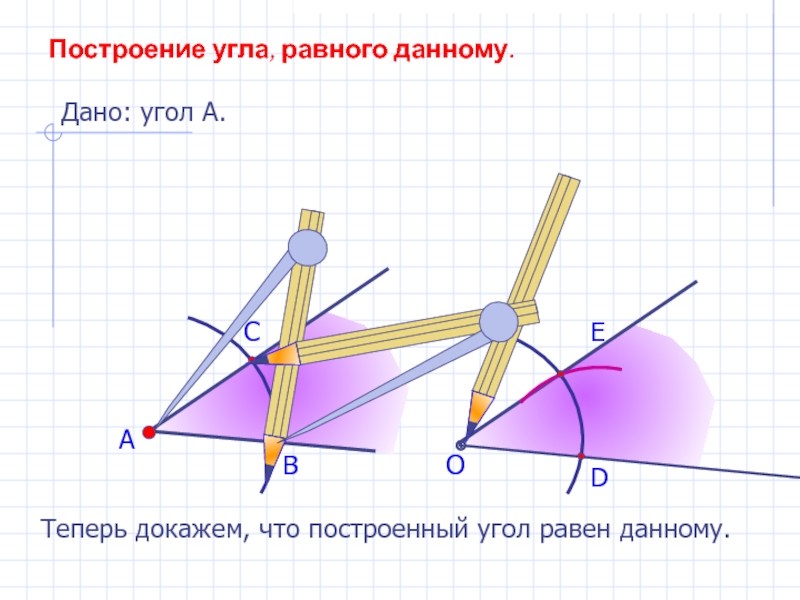
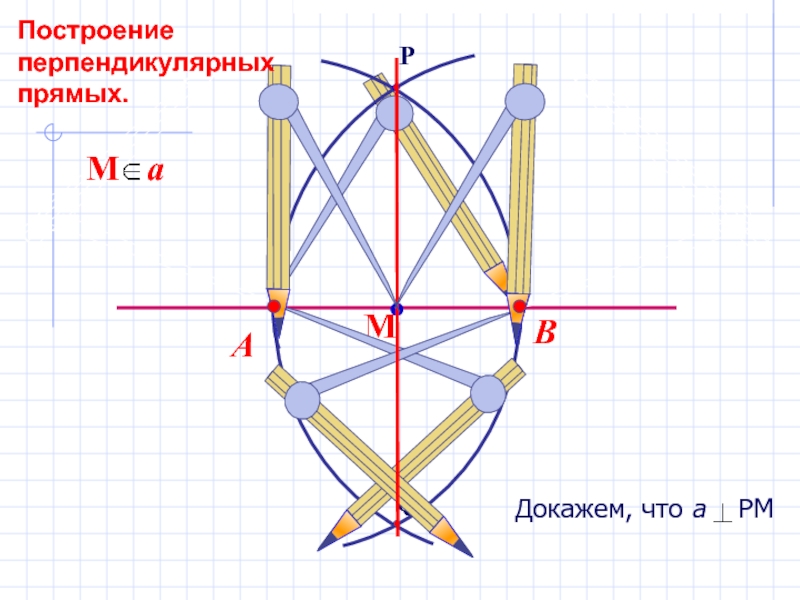
Построение угла, равного данному.
Дано: угол А.
О
D
E
Теперь докажем, что построенный угол
равен данному.
Слайд 9
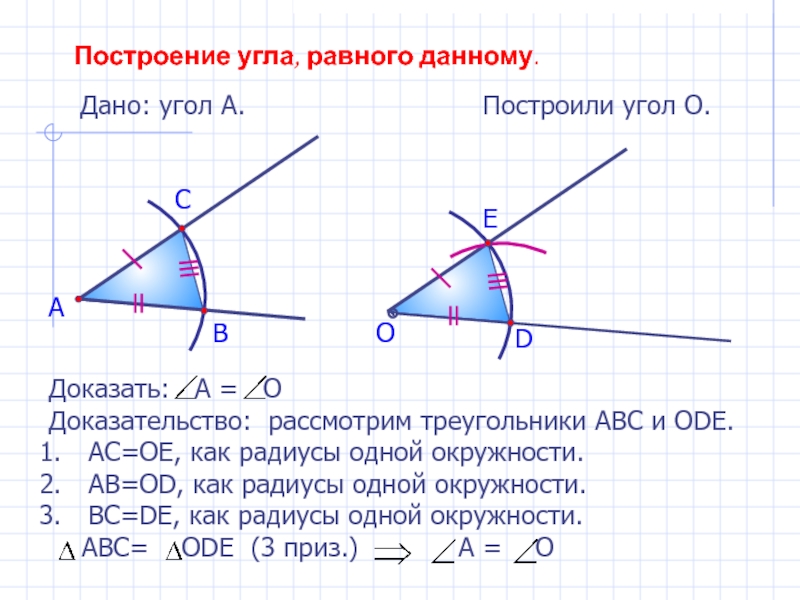
Построение угла, равного данному.
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А
= О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы
одной окружности.АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Слайд 11
Докажем, что луч АВ – биссектриса А
П Л А Н
Дополнительное построение.
Докажем равенство
треугольников ∆ АСВ и ∆ АDB.3. Выводы
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
Слайд 13Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как
радиусы одной окружности
АРВ р/б
3. РМ медиана в р/б
треугольнике является также ВЫСОТОЙ. Значит, а РМ.
М
a
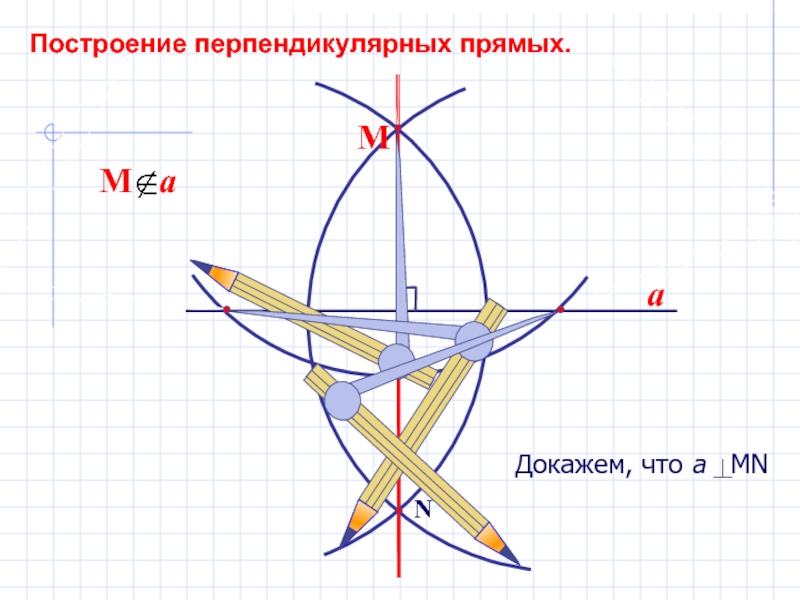
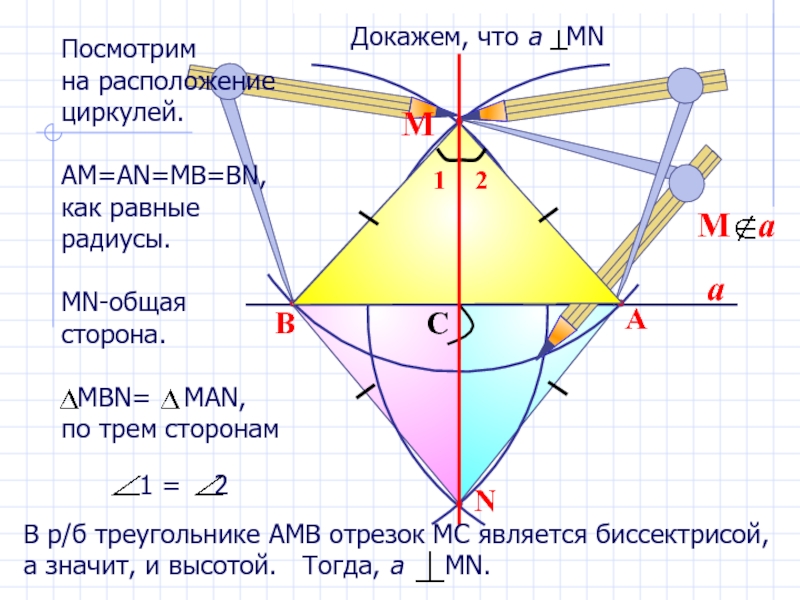
Слайд 15
a
N
B
A
C
М
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN= MAN,
по трем сторонам
Слайд 17
В
А
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.
Тогда, точка О – середина АВ.
Докажем, что О –
середина отрезка АВ.
Слайд 18
D
С
Построение треугольника по двум сторонам и углу между ними.
Угол
hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному.
Отложим
отрезок АС, равный P2Q2.В
А
Треугольник АВС искомый. Обоснуй, используя I признак.
Дано:
Отрезки Р1Q1 и Р2Q2
Q1
P1
P2
Q2
а
k
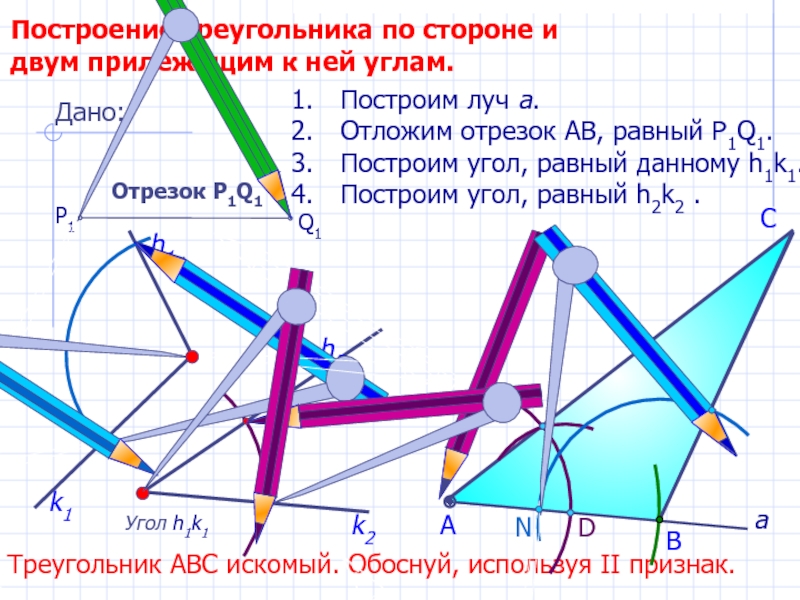
Слайд 19
D
С
Построение треугольника по стороне и двум прилежащим к ней углам.
Угол h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный
данному h1k1.Построим угол, равный h2k2 .
В
А
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
h1
k1
N
Слайд 20
С
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром
в т. А и
радиусом Р2Q2.
Построим дугу
с центром в т.В ирадиусом P3Q3.
В
А
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Построение треугольника по трем сторонам.
Слайд 21Подведение итогов урока
Оцените свою работу, выбрав один из вариантов ответа
Оцените
степень сложности урока.
Вам было на уроке:
легко
обычно
трудно
Оцените степень
вашего усвоения материала:усвоил полностью, могу применить
усвоил полностью, но затрудняюсь в применении
усвоил частично
не усвоил.