Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цилиндр. Конус. Шар 10-11 класс
Содержание
- 1. Цилиндр. Конус. Шар 10-11 класс
- 2. Презентация урока по геометрии на тему:"Цилиндр. Конус. Шар." МБОУ «Криушинская СОШ»учитель Погодина Г.Б.
- 3. ЦЕЛЬ УРОКА Рассмотреть геометрические тела – цилиндр,
- 4. άβLL1Тело, ограниченное цилиндрической поверхностью и двумя кругами
- 5. hABплощадь поверхности цилиндра rh2πrBAРазвертка цилиндраЗа площадь боковой
- 6. конус РrТело, ограниченное конической поверхностью и кругом
- 7. Площадь поверхности конуса За площадь боковой поверхности
- 8. Сфера и шар АВСферой называется поверхность, состоящая
- 9. Касательная плоскость к сфере ОАαТеорема:Радиус сферы, проведенный
- 10. Решение задач 1. Осевое сечение цилиндра -
- 11. Задание на дом §1,2,3Решить упражнения № 525, 547, 574Подведение итогов Выставление оценок
- 12. Скачать презентанцию
Презентация урока по геометрии на тему:"Цилиндр. Конус. Шар." МБОУ «Криушинская СОШ»учитель Погодина Г.Б.
Слайды и текст этой презентации
Слайд 3ЦЕЛЬ УРОКА
Рассмотреть геометрические тела – цилиндр, конус,
шар;
какими элементами они образованы;
виды сечений;
каким образом
вычисляются площади поверхностей данных фигур.Научить строить данные геометрические тела.
Научить применять полученные знания и умения при решении задач
Слайд 4
ά
β
L
L1
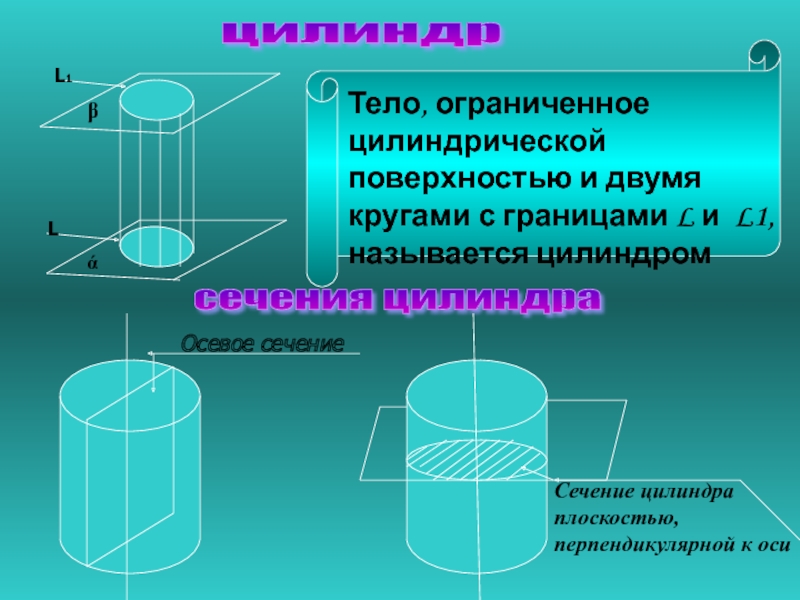
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L
и L1, называется цилиндром
сечения цилиндра
Осевое сечение
Сечение цилиндра плоскостью, перпендикулярной
к осицилиндр
Слайд 5
h
A
B
площадь поверхности цилиндра
r
h
2πr
B
A
Развертка цилиндра
За площадь боковой поверхности цилиндра принимается
площадь ее развертки, равная произведению длины окружности основания на высоту
цилиндра.Sбок = 2πrh
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
Sцил = 2πr² +2πrh = 2πr (r + h)
Слайд 6конус
Р
r
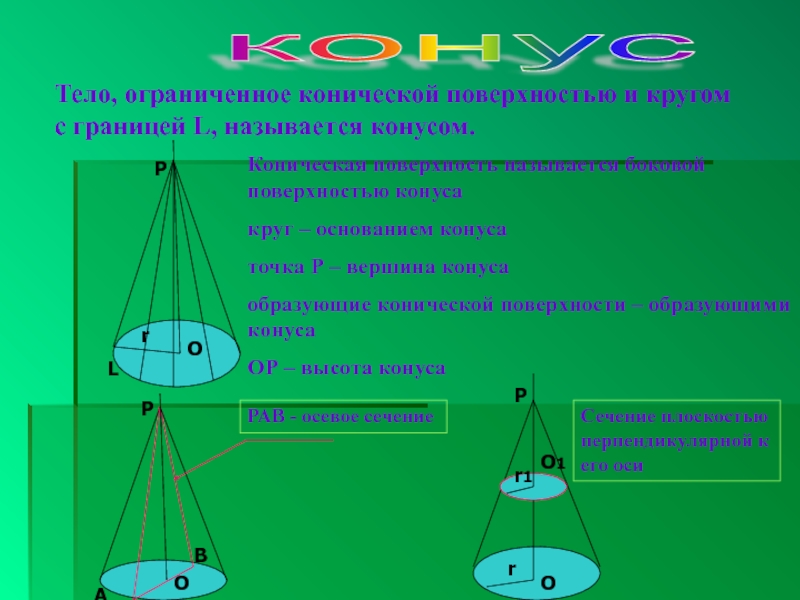
Тело, ограниченное конической поверхностью и кругом с границей L,
называется конусом.
L
О
Коническая поверхность называется боковой поверхностью конуса
круг – основанием
конусаточка Р – вершина конуса
образующие конической поверхности – образующими конуса
ОР – высота конуса
Р
О
А
В
РАВ - осевое сечение
Р
О
О1
r
r1
Сечение плоскостью перпендикулярной к его оси
Слайд 7Площадь поверхности конуса
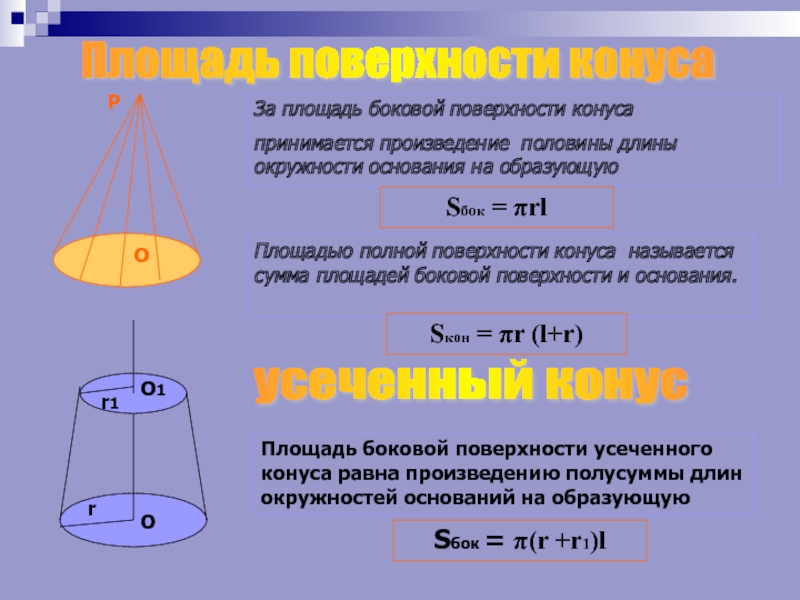
За площадь боковой поверхности конуса
принимается произведение
половины длины окружности основания на образующую
Sбок = πrl
Площадью полной поверхности
конуса называется сумма площадей боковой поверхности и основания. Sкон = πr (l+r)
Р
О
О
О1
r
r1
усеченный конус
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую
Sбок = π(r +r1)l
Слайд 8Сфера и шар
А
В
Сферой называется поверхность, состоящая из всех точек
пространства, расположенных на данном расстоянии от данной точки
Уравнение сферы
В
прямоугольной системе координат уравнение сферы радиуса R с центром С(x0;y0;z0) имеет вид (x-x0)²+(y-y0)²+(z+z0)²=R
α
x
y
z
Слайд 9Касательная плоскость к сфере
О
А
α
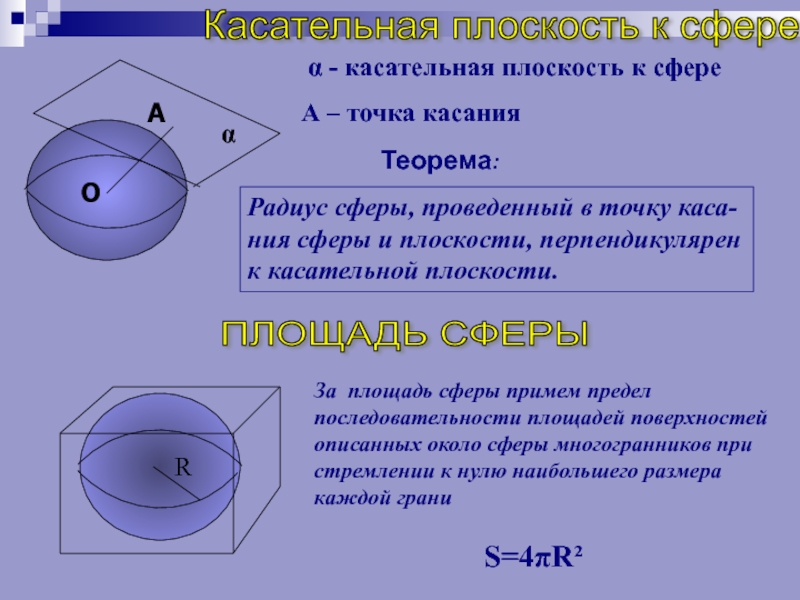
Теорема:
Радиус сферы, проведенный в точку каса-ния
сферы и плоскости, перпендикулярен к касательной плоскости.
α - касательная
плоскость к сфереА – точка касания
R
ПЛОЩАДЬ СФЕРЫ
За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани
S=4πR²
Слайд 10Решение задач
1. Осевое сечение цилиндра - квадрат, диагональ которого
равна 20 см. Найдите: а)высоту цилиндра; в) площадь основания цилиндра.
2. Найдите высоту конуса, если площадь его осевого сечения равна 6 дм², а площадь основания равна 8 дм².
3. Найдите уравнение сферы радиуса R с центром А, если а) А(2;-4;7), R=3; А(0;0;0), R=√2; в) А(2;0;0), R=4
