Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Три признака равенства треугольников
Содержание
- 1. Три признака равенства треугольников
- 2. Что такое треугольник?Треугольник — это простейший многоугольник,
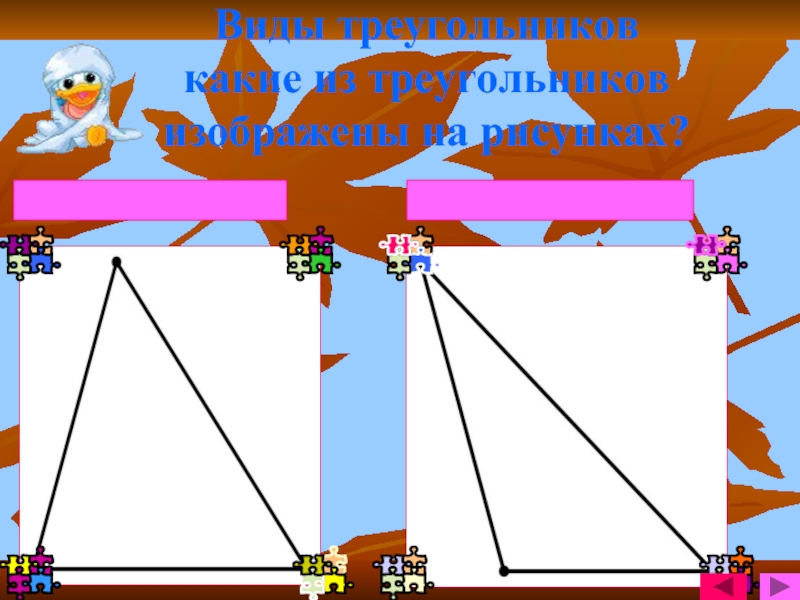
- 3. Виды треугольников какие из треугольников изображены на рисунках?остроугольныйтупоугольный
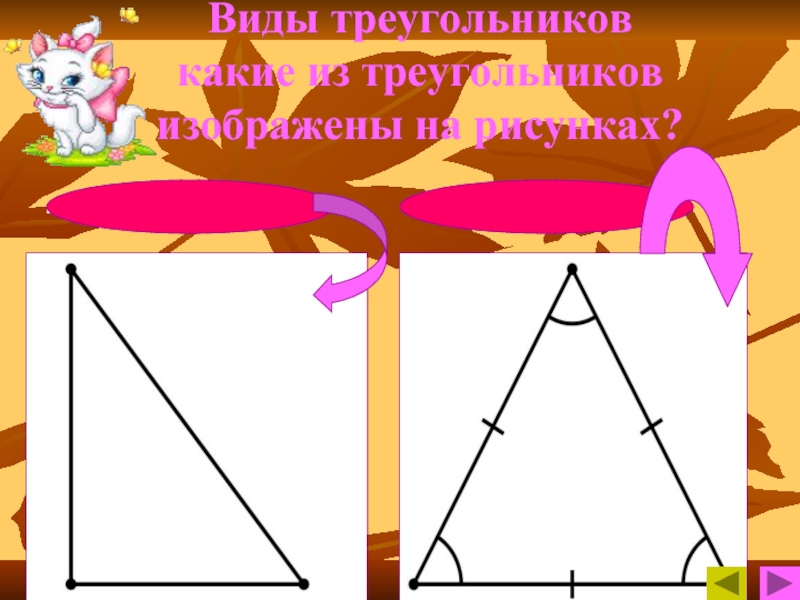
- 4. Виды треугольников какие из треугольников изображены на рисунках?прямоугольныйравносторонний
- 5. Виды треугольников какой треугольник изображён на рисунке?равнобедренный
- 6. Отрезок соединяющий вершину треугольника с серединой противоположной
- 7. Высота треугольникаПерпендикуляр проведенный из вершины треугольника к
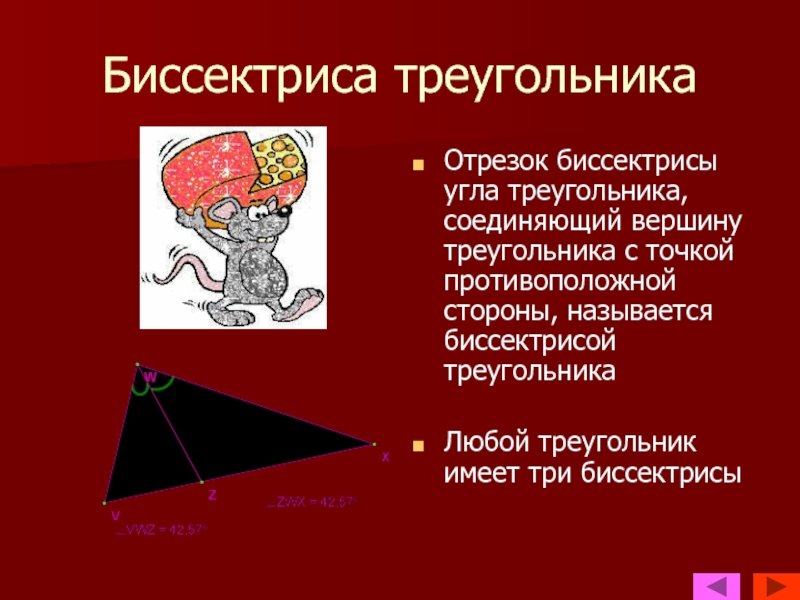
- 8. Биссектриса треугольникаОтрезок биссектрисы угла треугольника, соединяющий вершину
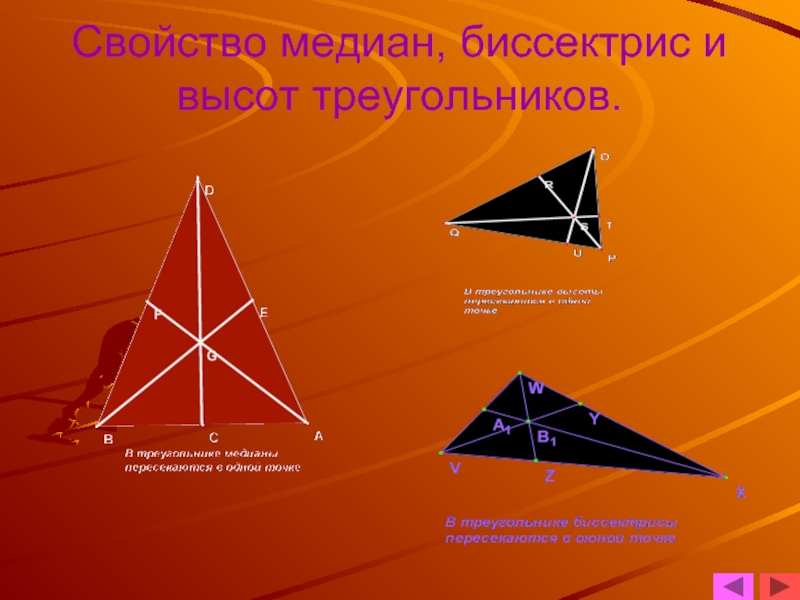
- 9. Свойство медиан, биссектрис и высот треугольников.
- 10. Физкультминутка
- 11. Первый признакЕсли две стороны и угол между
- 12. Второй признакЕсли сторона и два прилежащих угла
- 13. Третий признакЕсли три стороны одного треугольника соответственно
- 14. ЗаключениеЭту тему должны знать все: как дети
- 15. Желаю удачи!
- 16. Скачать презентанцию
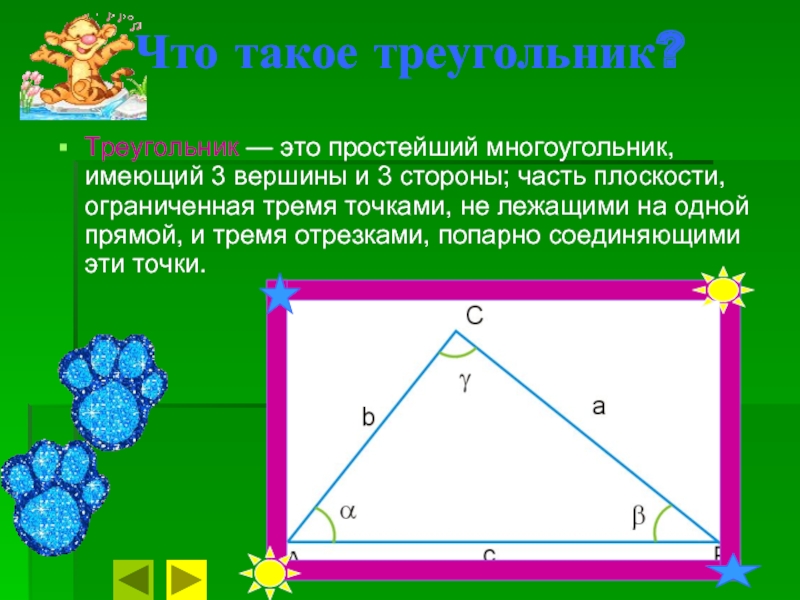
Что такое треугольник?Треугольник — это простейший многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Слайды и текст этой презентации
Слайд 1Презентация к исследовательской работе.
Три признака равенства треугольников
Подготовила ученица 10 класса
СОШ №19 г. Тимашевска
Слайд 2Что такое треугольник?
Треугольник — это простейший многоугольник, имеющий 3 вершины
и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими
на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Слайд 6
Отрезок соединяющий вершину треугольника с серединой противоположной стороны, называется медианой
треугольника.
Любой треугольник имеет три медианы.
Медиана треугольника
Слайд 7Высота треугольника
Перпендикуляр проведенный из вершины треугольника к прямой, содержащей противоположную.
Сторону, называется высотой треугольника
Любой треугольник имеет три высоты
Слайд 8Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой
противоположной стороны, называется биссектрисой треугольника
Любой треугольник имеет три биссектрисы
Слайд 11Первый признак
Если две стороны и угол между ними одного треугольника,
соответственно равны двум сторонам и углу между ними другого треугольника
, то такие треугольники равны
Слайд 12Второй признак
Если сторона и два прилежащих угла одного треугольника соответственно
равны стороне и двум прилежащим углам другого треугольника , то
такие треугольники равны.
Слайд 13Третий признак
Если три стороны одного треугольника соответственно равны трем сторонам
другого треугольника . То такие треугольники равны.
Слайд 14Заключение
Эту тему должны знать все: как дети так и их
родители.
Изучив подробно данную тему, мы сможем с легкостью решать сложные
задачки и конечно же доказывать теоремы.
Теги