Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Четыре замечательные точки треугольника 8 класс
Содержание
- 1. Четыре замечательные точки треугольника 8 класс
- 2. Точка пересечения медиан треугольникаТочка пересечения биссектрис треугольникаТочка пересечения высот треугольникаТочка пересечения серединных перпендикуляров треугольника
- 3. Медианой (BD) треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.АВСDМедиана
- 4. Медианы треугольника пересекаются в одной точке (центре
- 5. Биссектрисой (АD) треугольника называется отрезок биссектрисы внутреннего угла треугольника.
- 6. Каждая точка биссектрисы неразвёрнутого угла равноудалена от
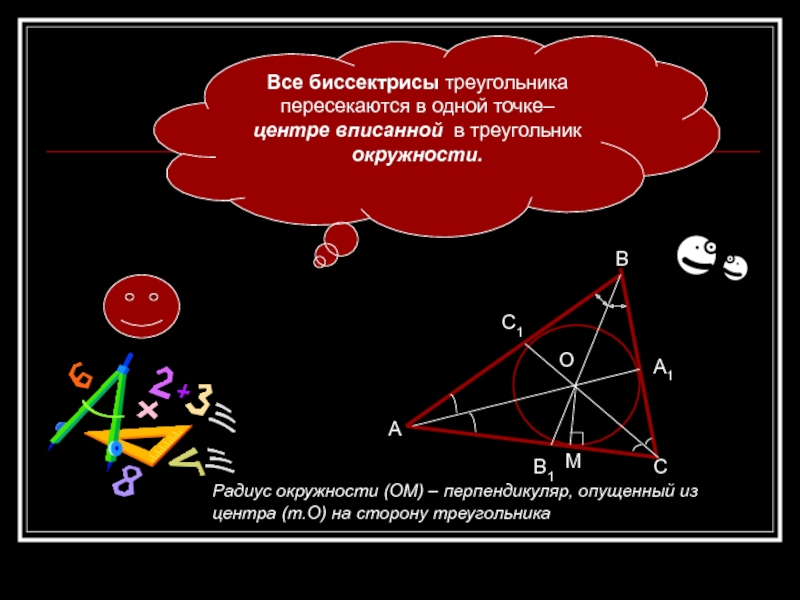
- 7. Все биссектрисы треугольника пересекаются в одной точке–
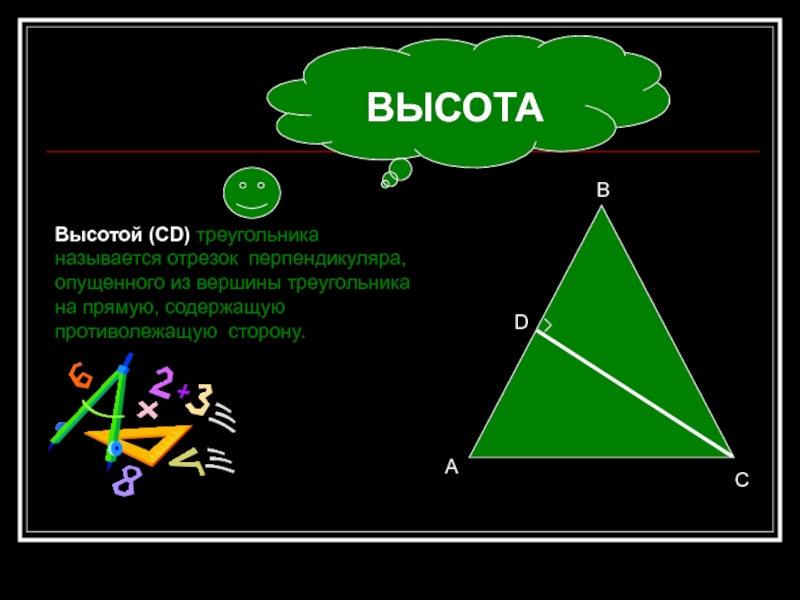
- 8. ВЫСОТАВысотой (СD) треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на прямую, содержащую противолежащую сторону.ABCD
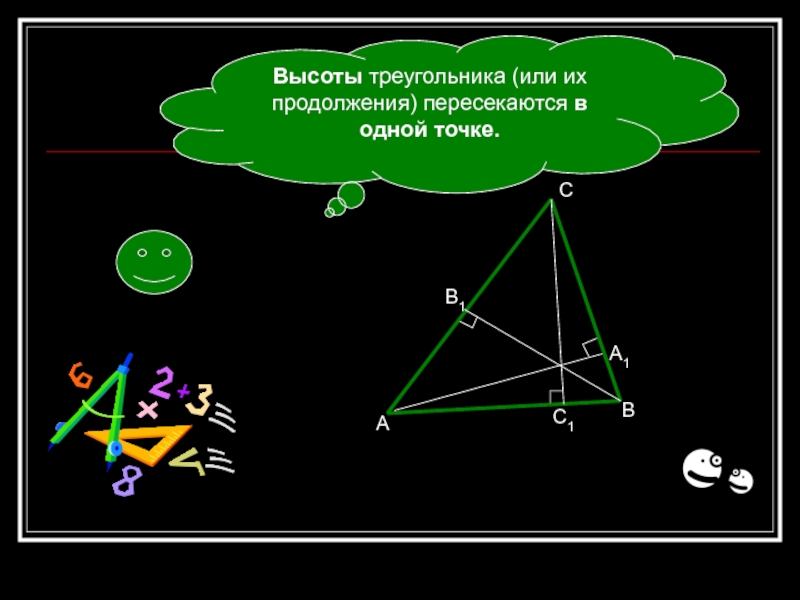
- 9. Высоты треугольника (или их продолжения) пересекаются в одной точке.АА1ВВ1СС1
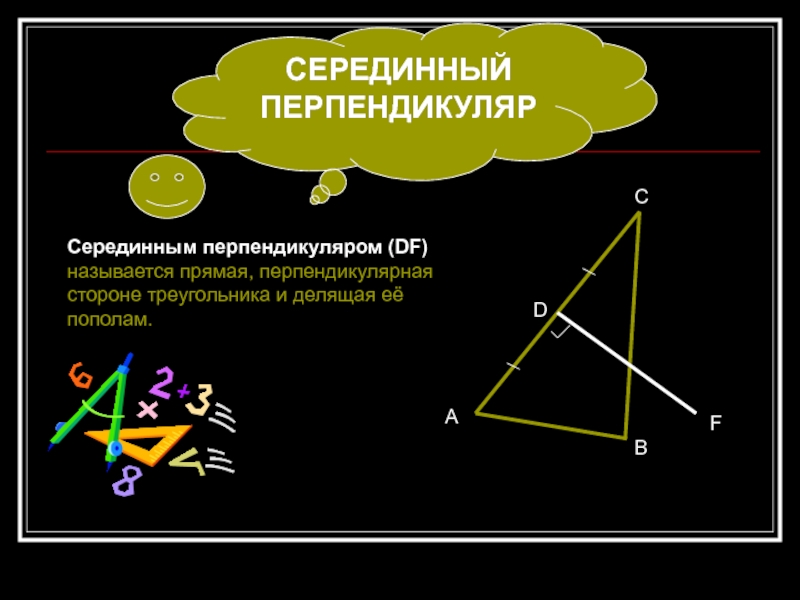
- 10. СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯРСерединным перпендикуляром (DF) называется прямая, перпендикулярная стороне треугольника и делящая её пополам.АDFBC
- 11. АМВmOКаждая точка серединного перпендикуляра (m) к отрезку
- 12. Все серединные перпендикуляры сторон треугольника пересекаются в
- 13. Задания для учащихсяПостройте с помощью циркуля и
- 14. 2. Постройте с помощью циркуля и линейки
- 15. Скачать презентанцию
Точка пересечения медиан треугольникаТочка пересечения биссектрис треугольникаТочка пересечения высот треугольникаТочка пересечения серединных перпендикуляров треугольника
Слайды и текст этой презентации
Слайд 2
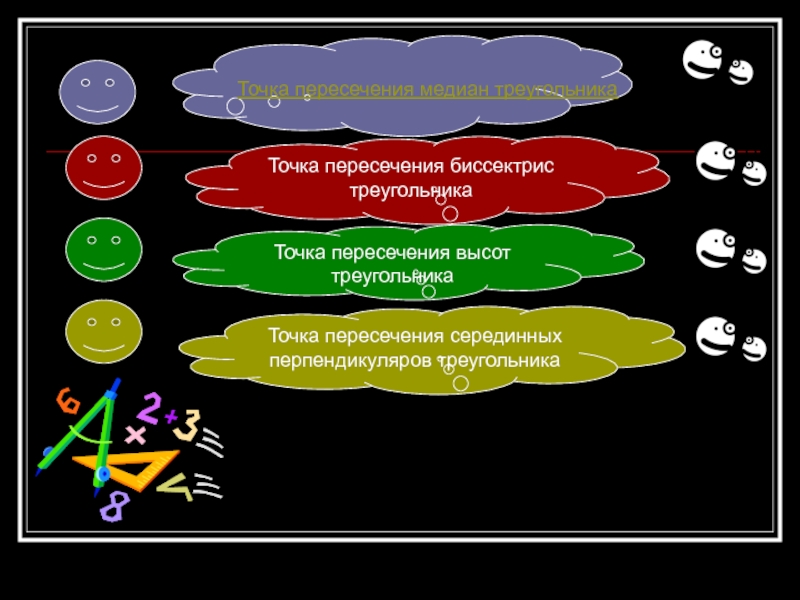
Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Точка пересечения высот треугольника
Точка
пересечения серединных перпендикуляров треугольника
Слайд 3 Медианой (BD) треугольника называется отрезок, который соединяет вершину
треугольника с серединой противолежащей стороны.
А
В
С
D
Медиана
Слайд 4
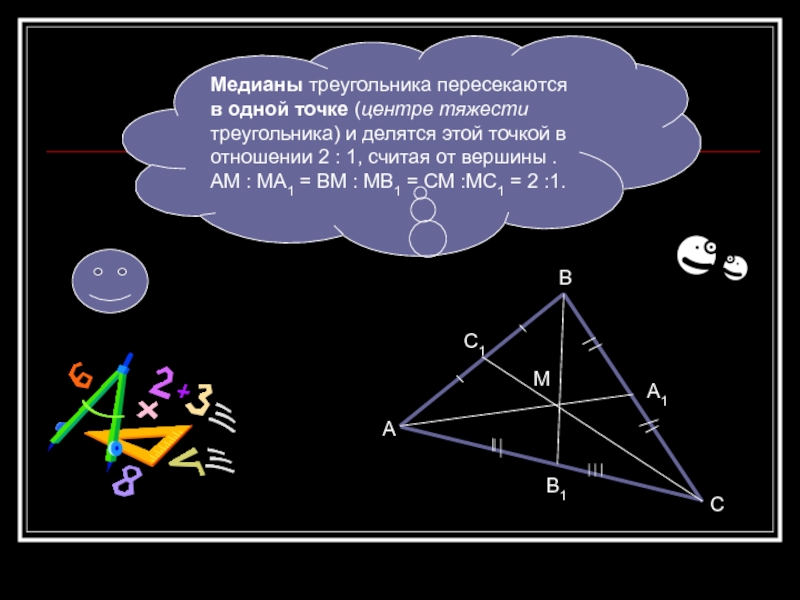
Медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и
делятся этой точкой в отношении 2 : 1, считая от
вершины .АМ : МА1 = ВМ : МВ1 = СМ :МС1 = 2 :1.
А
А1
В
В1
М
С
С1
Слайд 5
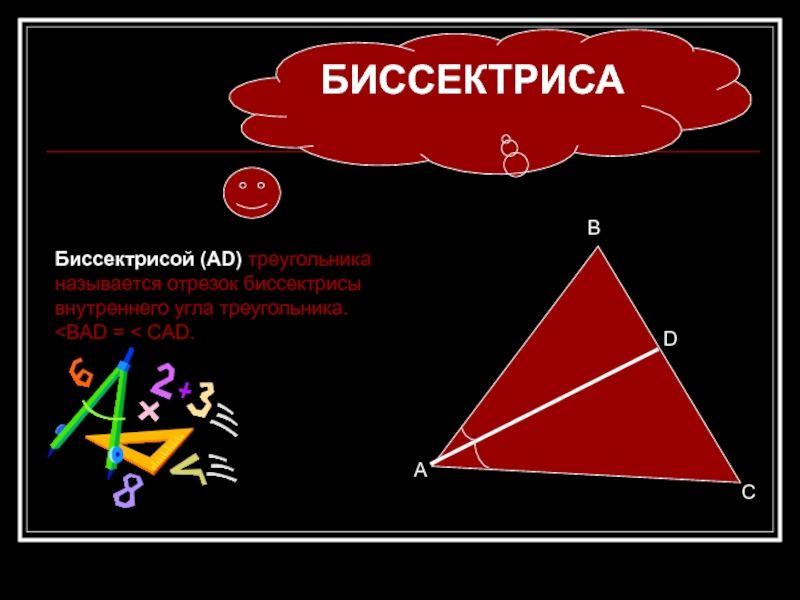
Биссектрисой (АD) треугольника называется отрезок биссектрисы внутреннего угла треугольника.
= < CAD.
C
БИССЕКТРИСА
A
D
В
Слайд 6
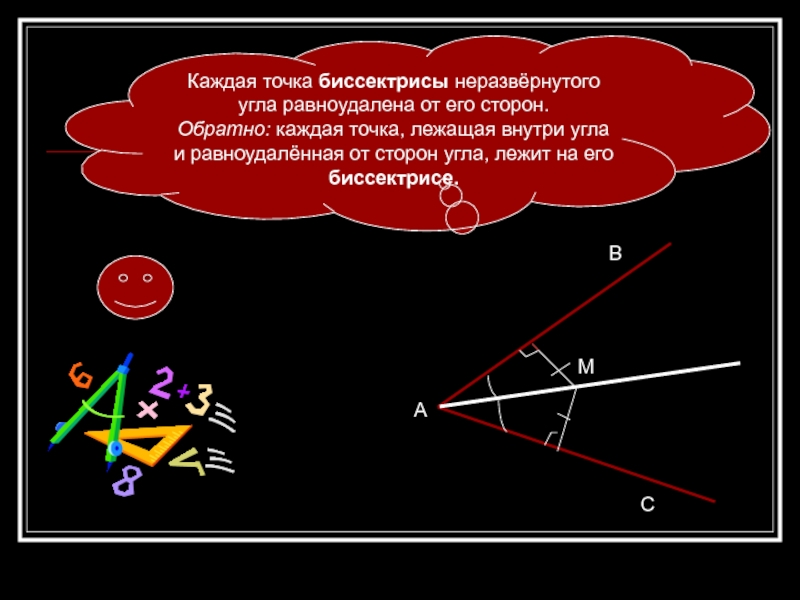
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Обратно: каждая
точка, лежащая внутри угла и равноудалённая от сторон угла, лежит
на его биссектрисе.А
М
В
С
Слайд 7
Все биссектрисы треугольника пересекаются в одной точке– центре вписанной в
треугольник окружности.
С
В1
М
Радиус окружности (ОМ) – перпендикуляр, опущенный из центра (т.О)
на сторону треугольникаСлайд 8
ВЫСОТА
Высотой (СD) треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника
на прямую, содержащую противолежащую сторону.
A
B
C
D
Слайд 10
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Серединным перпендикуляром (DF) называется прямая, перпендикулярная стороне треугольника и
делящая её пополам.
А
D
F
B
C
Слайд 11
А
М
В
m
O
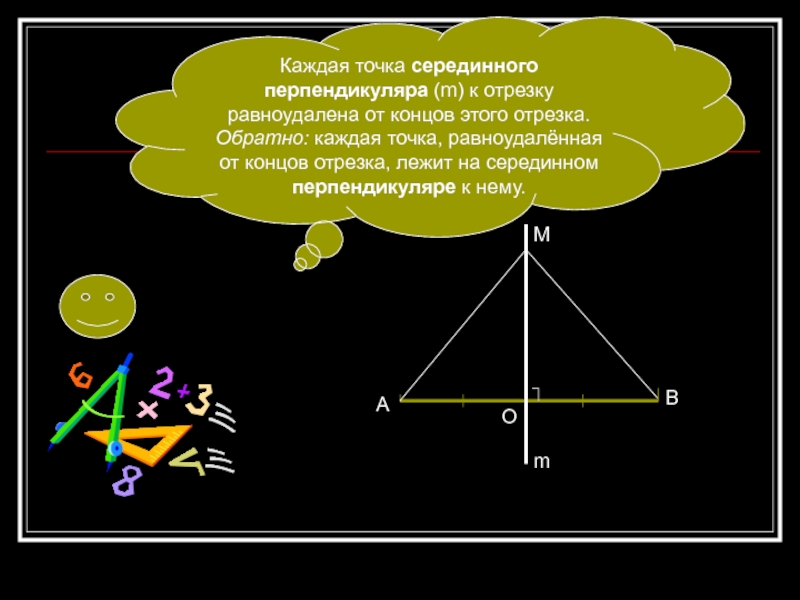
Каждая точка серединного перпендикуляра (m) к отрезку равноудалена от концов
этого отрезка.
Обратно: каждая точка, равноудалённая от концов отрезка, лежит
на серединном перпендикуляре к нему.Слайд 12
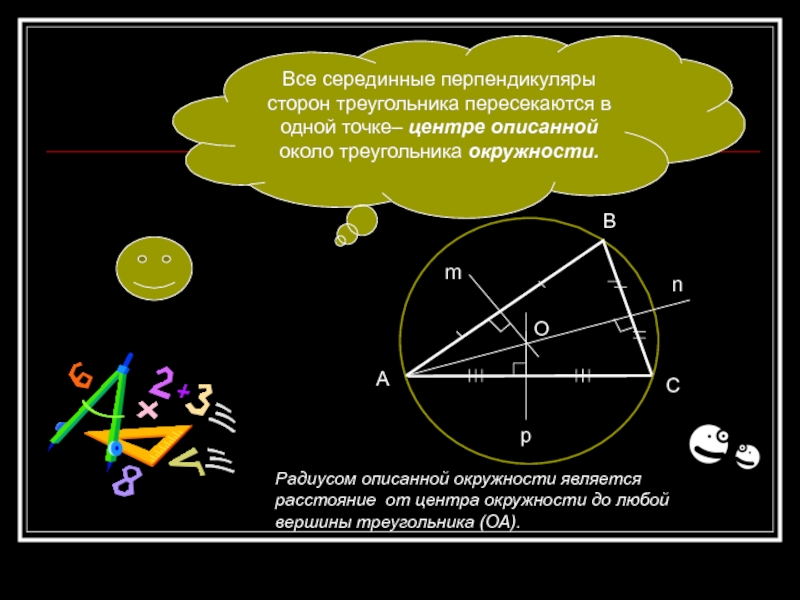
Все серединные перпендикуляры сторон треугольника пересекаются в одной точке– центре
описанной около треугольника окружности.
А
В
С
О
Радиусом описанной окружности является расстояние от центра
окружности до любой вершины треугольника (ОА). m
n
p
Слайд 13
Задания для учащихся
Постройте с помощью циркуля и линейки окружность, вписанную
в тупоугольный треугольник.
Для этого:
Постройте биссектрисы в тупоугольном треугольнике с помощью
циркуля и линейки. Точка пересечения биссектрис– центр окружности.Постройте радиус окружности: перпендикуляр из центра окружности на сторону треугольника.
Постройте окружность, вписанную в треугольник.
Слайд 14
2. Постройте с помощью циркуля и линейки окружность, описанную
около
тупоугольного треугольника.
Для этого:
Постройте серединные перпендикуляры к сторонам тупоугольного треугольника. Точка
пересечения этих перпендикуляров– центр описанной окружности.Радиус окружности– расстояние от центра до любой вершины треугольника.
Постройте окружность, описанную около треугольника.