Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач на вычисление площадей фигур
Содержание
- 1. Решение задач на вычисление площадей фигур
- 2. ЦЕЛИ УРОКА: закрепить теоретический материал по теме
- 3. Проверка домашнего задания№476, №478, №481, №474
- 4. №478Дано:ABCD –выпуклый четырехугольник, AC⊥BD Доказать: SABCD=½AC·BD РешениеSABCD
- 5. №476Дано:ABCD – ромб, AC⊥BD, AC=2дм, BD=4,6дм. Доказать:
- 6. HДано: ∆ABC, BM-медиана Сравнить: S∆ABM и S∆BMCРешение.
- 7. №481Дано:ABCD –трапеция, AD⊥AB, AB=BC=6см, ∠BCD=135° Найти: SABCDРешениеSABCD=½(AD+BC)·ABТак
- 8. Решение задач на готовых чертежах
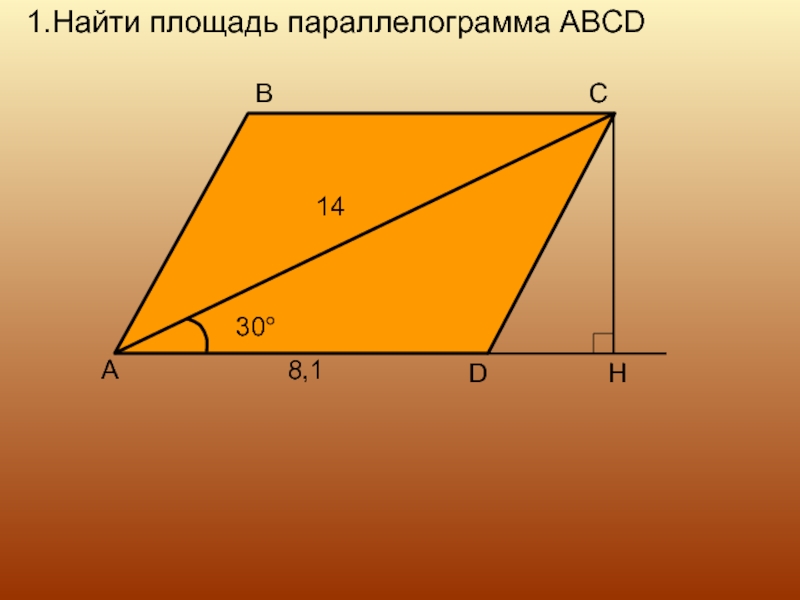
- 9. 1.Найти площадь параллелограмма ABCDH
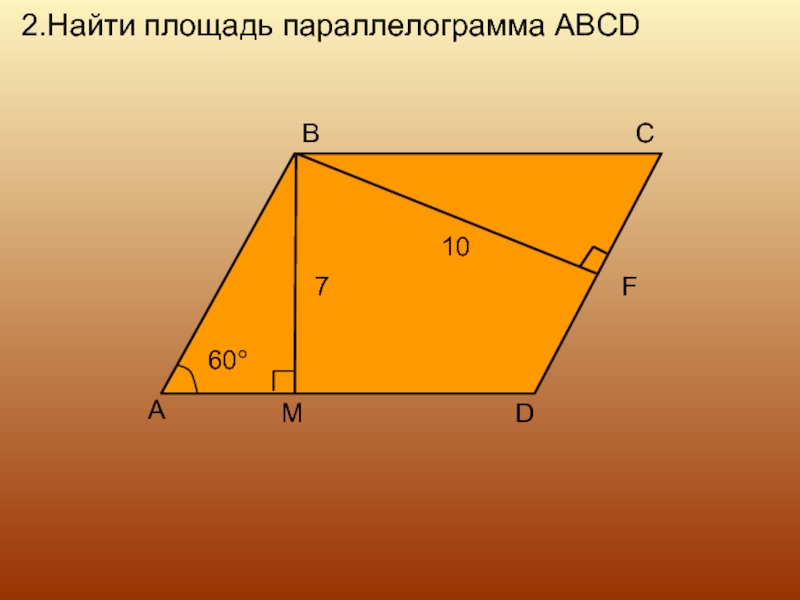
- 10. 2.Найти площадь параллелограмма ABCD
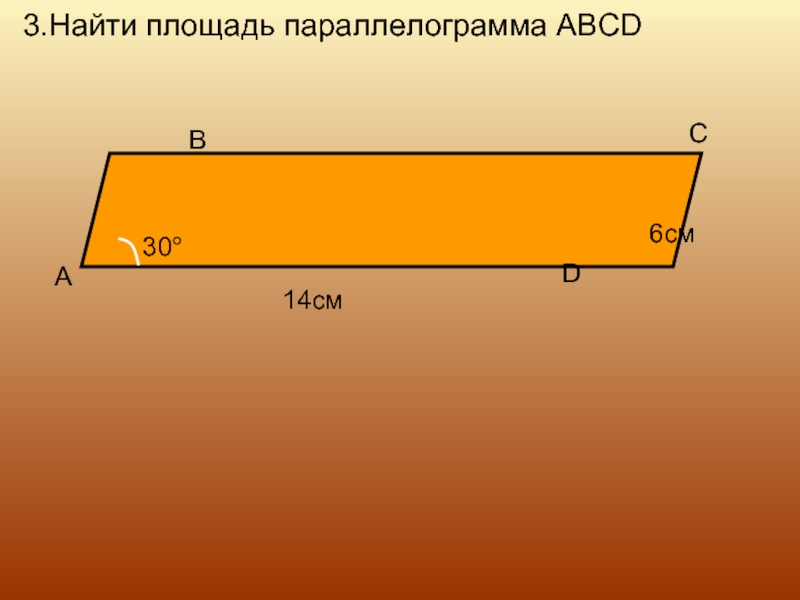
- 11. 3.Найти площадь параллелограмма ABCD
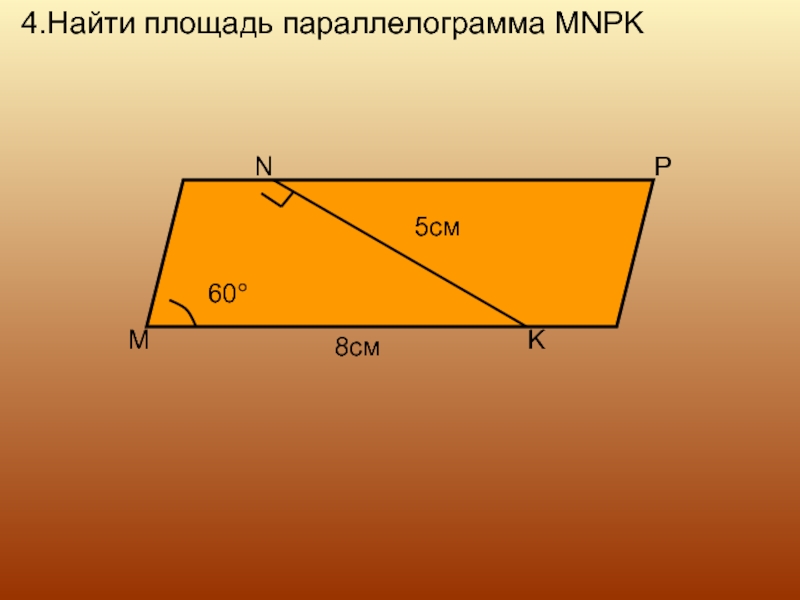
- 12. 4.Найти площадь параллелограмма MNPK
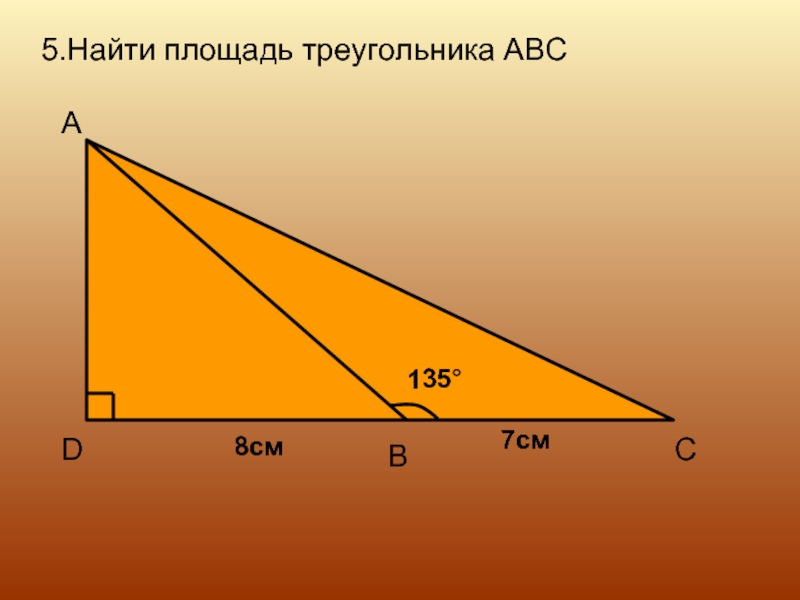
- 13. 5.Найти площадь треугольника ABC
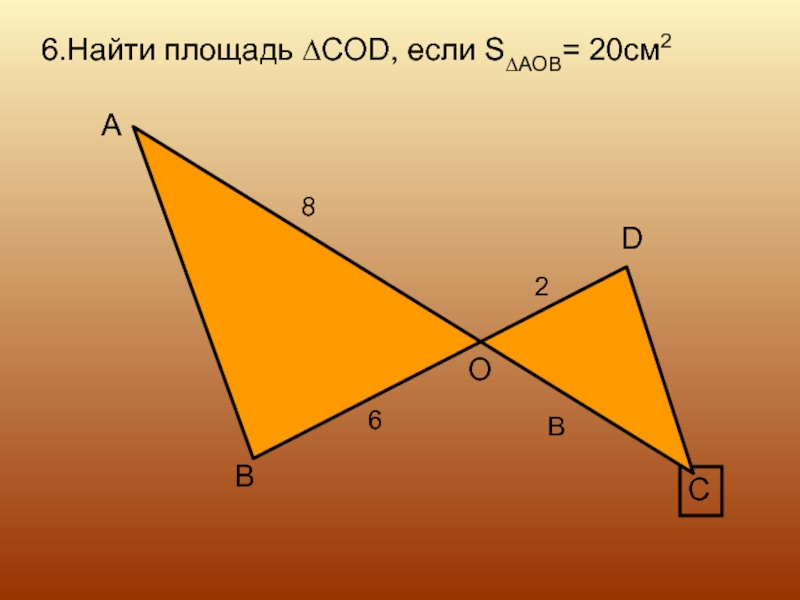
- 14. 6.Найти площадь ∆COD, если S∆AOB= 20см2
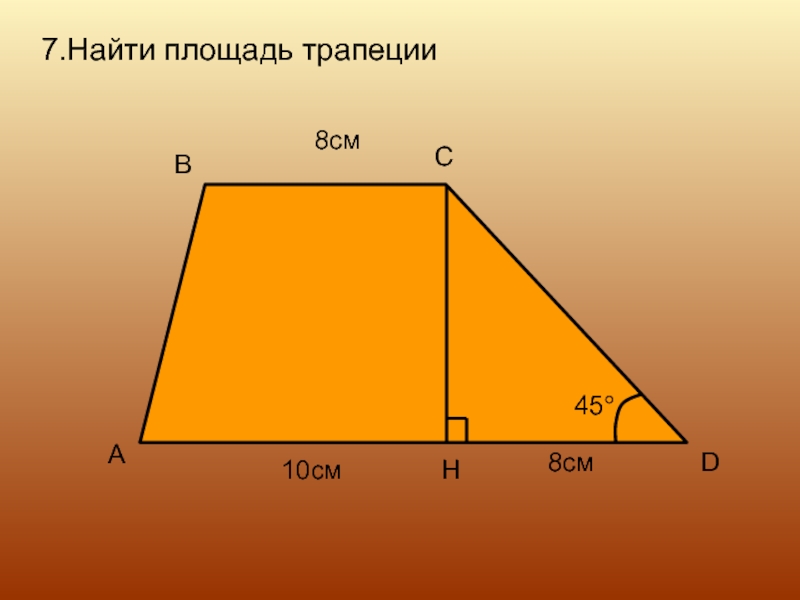
- 15. 7.Найти площадь трапеции
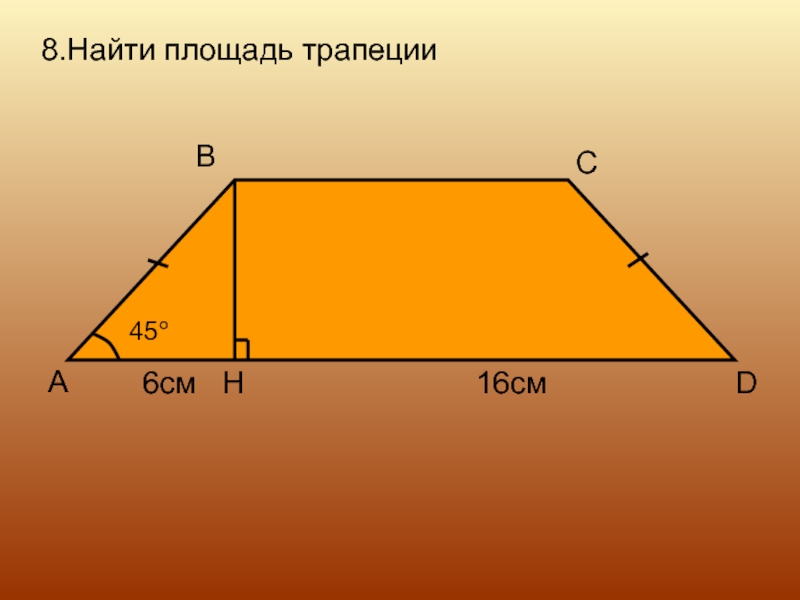
- 16. 8.Найти площадь трапеции
- 17. Самостоятельная работа Проверка выполнения работы
- 18. Вариант 11.5см10смS=½·a·h; h=2·5=10S=½·5·10=25см2Вариант 21.6см18смS=½·a·h; h=18:3=6S=½·18·6=54см2
- 19. Вариант 1Вариант 22.2.30º8см6смS = a·h; h =
- 20. Вариант 1Вариант 23.3.11cм7cм45ºS=½·(a+b)·h;h=4; S=½·(11+7)·4; S=36см245º20cм6cм8cмS=½·(a+b)·h; h=6; b=2O-2·6=8; S=½·(2O+8)·6=84см2
- 21. Вариант 1№4.HЕсли высоты двух треугольников равны, то
- 22. ΔMBC и ΔMCK имеют общую высоту MN,
- 23. Вариант 2№4.HKЕсли высоты двух треугольников равны, то
- 24. ДОМАШНЕЕ ЗАДАНИЕ:№ 466, 467, 476 б, №44 (рт)
- 25. Скачать презентанцию
ЦЕЛИ УРОКА: закрепить теоретический материал по теме «Площадь»; совершенствовать навыки решения задач на вычисление площадей фигур.
Слайды и текст этой презентации
Слайд 1Решение задач на вычисление площадей фигур
Подготовила учитель математики
МОУ
СОШ №4 города Чаплыгина
Слайд 2ЦЕЛИ УРОКА:
закрепить теоретический материал по теме «Площадь»;
совершенствовать навыки
решения задач на вычисление площадей фигур.
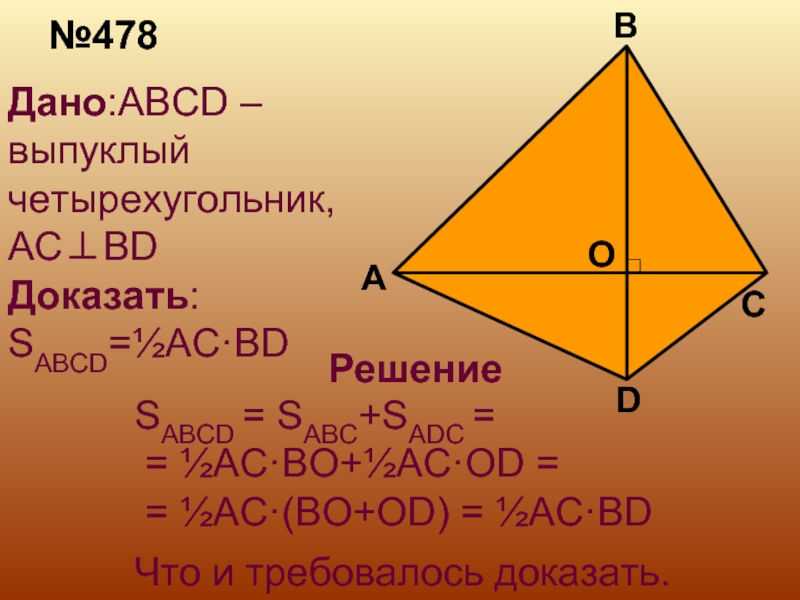
Слайд 4№478
Дано:ABCD –выпуклый четырехугольник, AC⊥BD
Доказать: SABCD=½AC·BD
Решение
SABCD = SABC+SADC =
= ½AC·BO+½AC·OD =
= ½AC·(BO+OD) = ½AC·BD
Что и требовалось
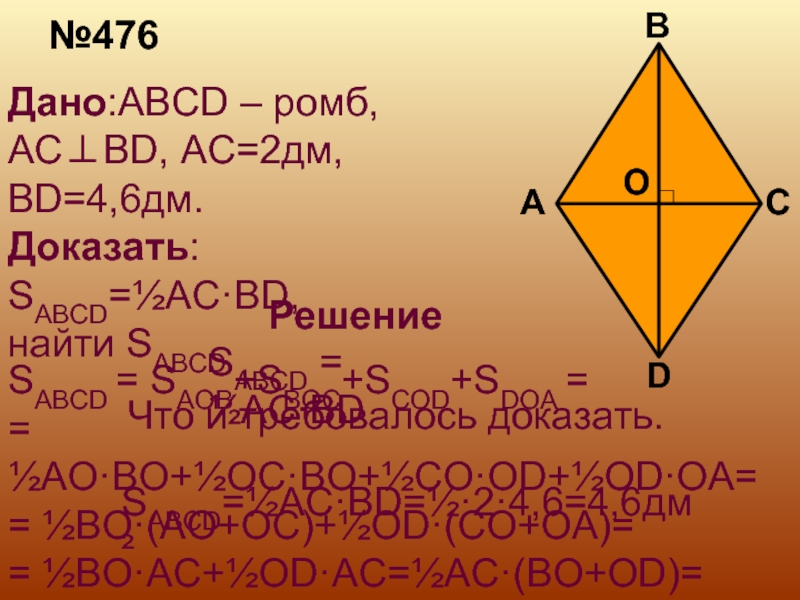
доказать. Слайд 5№476
Дано:ABCD – ромб, AC⊥BD, AC=2дм, BD=4,6дм.
Доказать: SABCD=½AC·BD,
найти SABCD
Решение
SABCD
= SAOB+SBOC+SCOD+SDOA =
= ½AO·BO+½OC·BO+½CO·OD+½OD·OA=
= ½BO·(AO+OC)+½OD·(CO+OA)=
= ½BO·AC+½OD·AC=½AC·(BO+OD)=
SABCD = ½AC·BD
Что
и требовалось доказать. SABCD=½AC·BD=½·2·4,6=4,6дм²
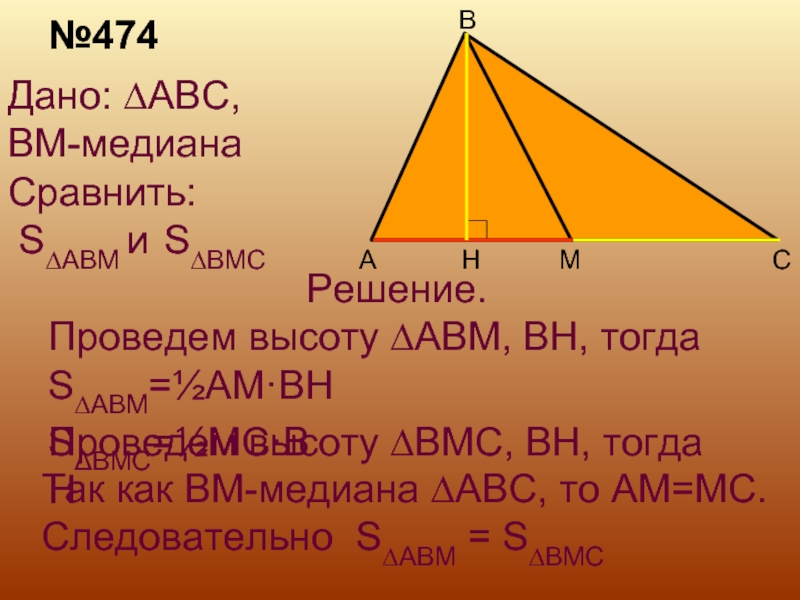
Слайд 6H
Дано: ∆ABC,
BM-медиана
Сравнить:
S∆ABM и S∆BMC
Решение.
Проведем высоту ∆ABM,
BH, тогда S∆ABM=½AM·BH
Так как BM-медиана ∆ABC, то AM=MC.
Следовательно S∆ABM =
S∆BMC№474
Проведем высоту ∆BMC, BH, тогда
SΔBMC=½MC·BH
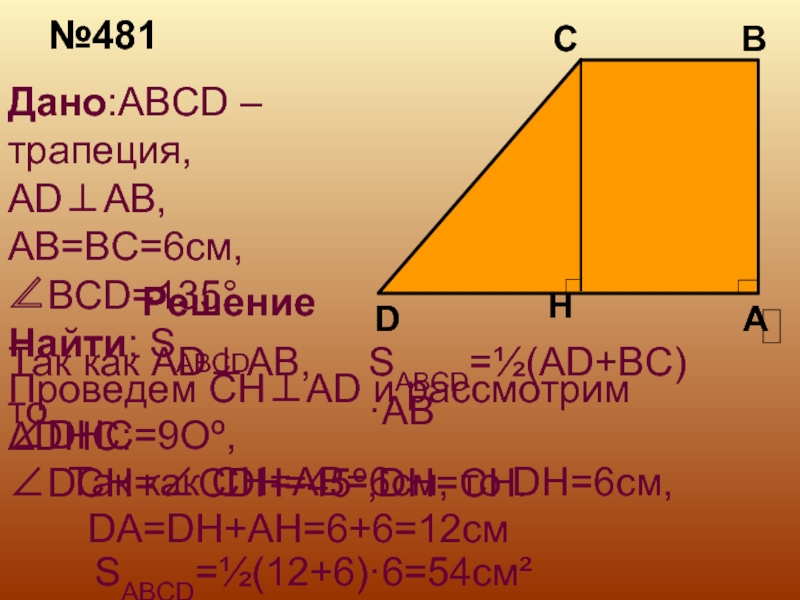
Слайд 7№481
Дано:ABCD –трапеция, AD⊥AB, AB=BC=6см, ∠BCD=135°
Найти: SABCD
Решение
SABCD=½(AD+BC)·AB
Так как AD⊥AB, то
H
Проведем
CH⊥AD и рассмотрим ΔDHC:
∠DHC=9Oº,∠DCH=∠CDH=45º,DH=CH.
Так как CH=AB=6см, то DH=6см,
DA=DH+AH=6+6=12см
SABCD=½(12+6)·6=54см²
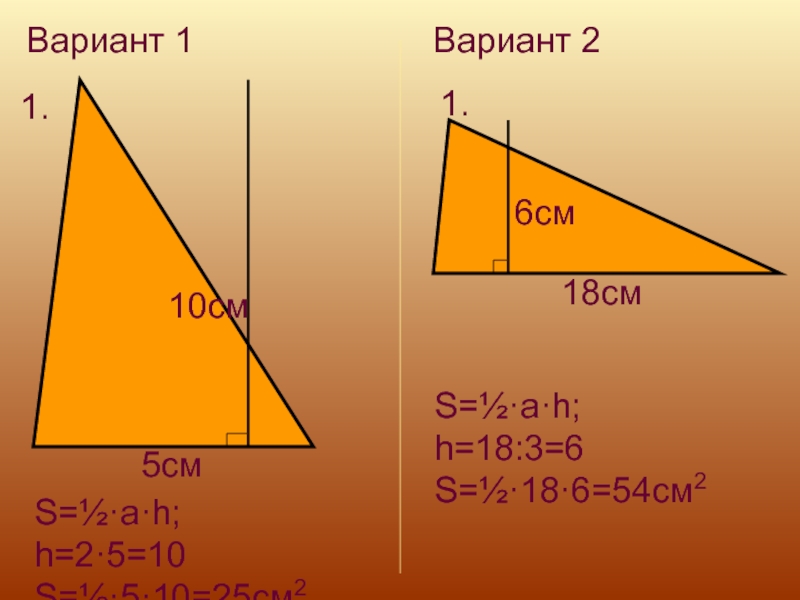
Слайд 18Вариант 1
1.
5см
10см
S=½·a·h; h=2·5=10
S=½·5·10=25см2
Вариант 2
1.
6см
18см
S=½·a·h; h=18:3=6
S=½·18·6=54см2
Слайд 19Вариант 1
Вариант 2
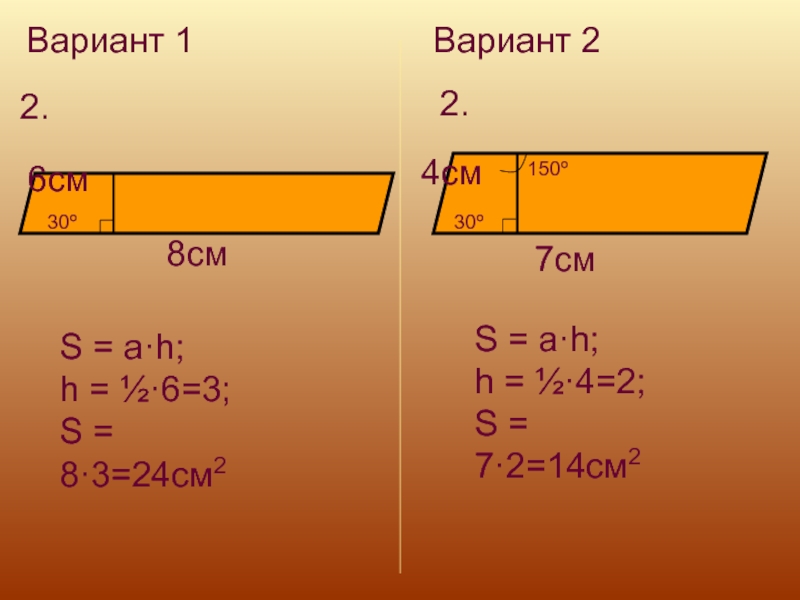
2.
2.
30º
8см
6см
S = a·h;
h = ½·6=3;
S =
8·3=24см2
30º
150º
S = a·h;
h = ½·4=2;
S = 7·2=14см2
7см
4см
Слайд 20Вариант 1
Вариант 2
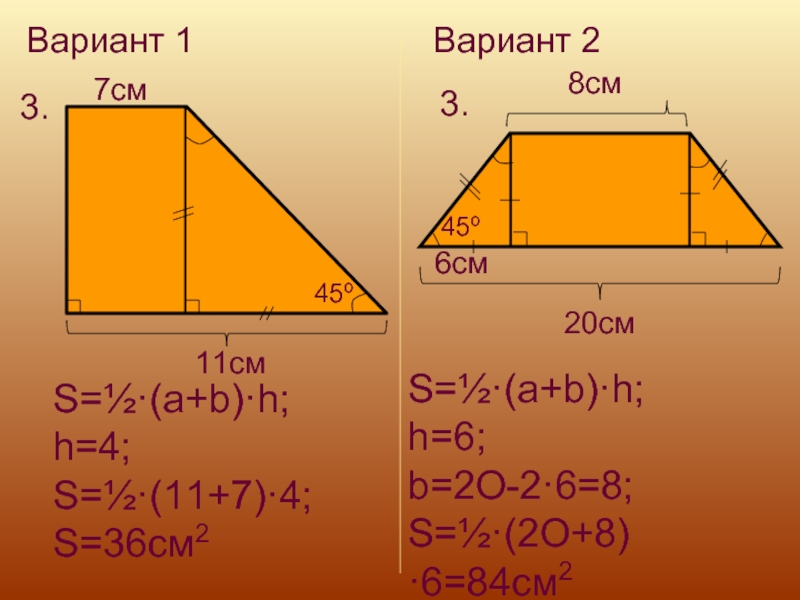
3.
3.
11cм
7cм
45º
S=½·(a+b)·h;
h=4;
S=½·(11+7)·4;
S=36см2
45º
20cм
6cм
8cм
S=½·(a+b)·h;
h=6;
b=2O-2·6=8;
S=½·(2O+8)·6=84см2
Слайд 21Вариант 1
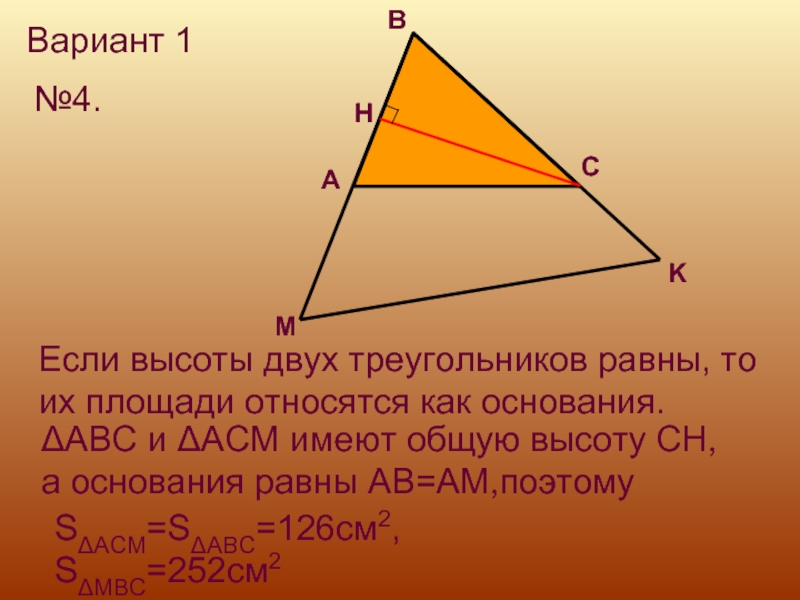
№4.
H
Если высоты двух треугольников равны, то
их площади относятся
как основания.
ΔABC и ΔACM имеют общую высоту CH,
а основания
равны AB=AM,поэтомуSΔACM=SΔABC=126см2, SΔMBC=252см2
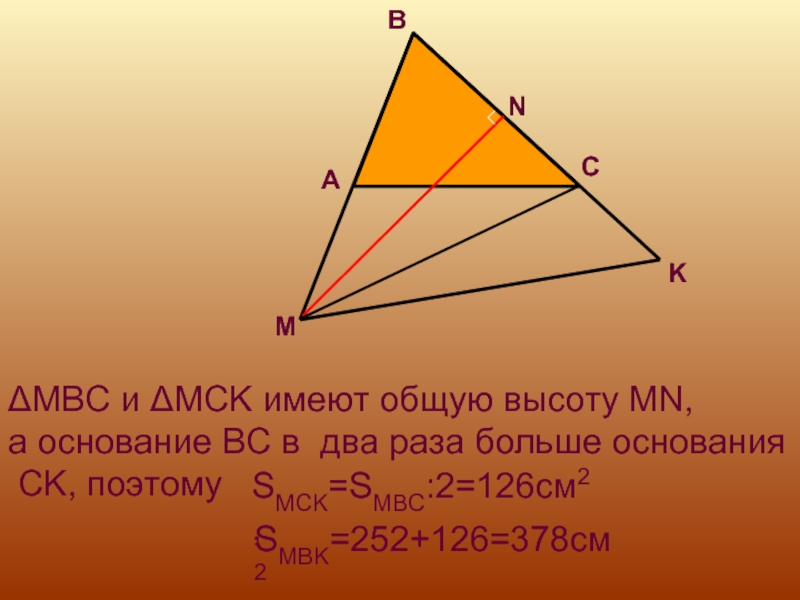
Слайд 22ΔMBC и ΔMCK имеют общую высоту MN,
а основание BC
в два раза больше основания
CK, поэтому
SMCK=SMBC:2=126см2,
SMBK=252+126=378см2
N
Слайд 23Вариант 2
№4.
H
K
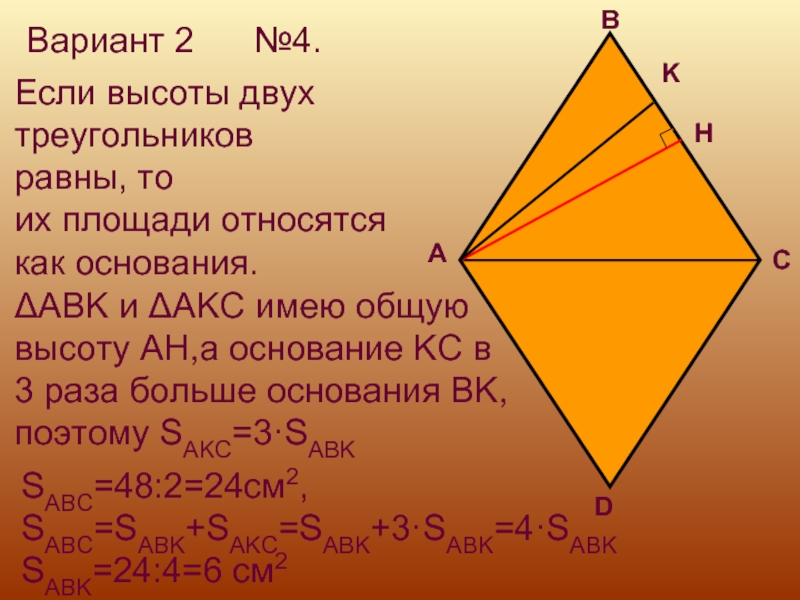
Если высоты двух
треугольников
равны, то
их площади относятся
как основания.
ΔABK и ΔAKC имею общую
высоту AH,а основание KC
в 3 раза больше основания BK,
поэтому SAKC=3·SABK
SABC=48:2=24см2,
SABC=SABK+SAKC=SABK+3·SABK=4·SABK
SABK=24:4=6 см2
Теги