Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения задач ЕГЭ по геометрии (стереометрия)
Содержание
- 1. Методы решения задач ЕГЭ по геометрии (стереометрия)
- 2. УЧЕБНО –МЕТОДИЧЕСКИЙ КОМПЛЕКТ 10-11 КЛАССГеометрия. Углубленный уровень.
- 3. К УЧЕБНО– МЕТОДИЧЕСКОМУ
- 4. Стереометрия. Задача 14 ЕГЭ
- 5. Задачи на нахождения расстояния между скрещивающимися прямыми
- 6. Способы нахождения расстояния между скрещивающимися прямымиРасстояние между
- 7. Способы нахождения расстояния между скрещивающимися прямымиРасстояние между
- 8. Способы нахождения расстояния между скрещивающимися прямымиМетод ортогонального
- 9. Задача № 4087 Дан куб
- 10. Решение:1.2.3.
- 11. Решение:4.
- 12. Решение:5.
- 13. Решение:6.
- 14. Решение:
- 15. Решение:8.
- 16. Решение:9.
- 17. Технологии, используемые
- 18. Технологии, используемые
- 19. Технологии, используемые
- 20. Задача 1В правильной треугольной призме все ребра
- 21. Решениеа) способ первый
- 22. Решениеа) способ второй
- 23. Решениеб) найти расстояние между прямыми и
- 24. МЕТОД КООРДИНАТ В ЗАДАЧАХ ЕГЭ
- 25. МЕТОД КООРДИНАТ В ЗАДАЧАХ ЕГЭ
- 26. МЕТОД КРДИНАТ В ЗАДАЧАХ
- 27. Задача 2В единичном кубе ABCDA1 B1C1D1 найдите
- 28. Задача 3Дана правильная четырехугольная призма ABCDA1B1C1D1 со
- 29. Площадь ортогональной проекции многоугольникаПлощадь ортогональной проекции многоугольника
- 30. Задача 4В правильной треугольной призме, каждое ребро
- 31. Краткое описание методикиНастоящая методика основана на реализации
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Методы решения задач ЕГЭ по геометрии (стереометрия)
Учитель математики Ланцов
Д.И.
(из опыта работы)Слайд 2УЧЕБНО –МЕТОДИЧЕСКИЙ КОМПЛЕКТ 10-11 КЛАСС
Геометрия. Углубленный уровень. 10-11 класс.: Учебник/
Е.В. Потоскуев, Л.И. Звавич
Геометрия. Углубленный уровень. 10-11 класс.: Задачник/ Е.В.
Потоскуев, Л.И. ЗвавичСлайд 3 К УЧЕБНО– МЕТОДИЧЕСКОМУ КОМПЛЕКТУ 10-11 КЛАСС
Геометрия. 8-11 кл.: пособие для школ и классов с углубленным
изучением математики /Л.И. Звавич, М.В. Шляпочник.Контрольные работы по геометрии. 10-11 класс /Е.В. Потоскуев, Л.И. Звавич.
ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14. (профильный уровень)/ Гордин Р.К. под редакцией И.В. Ященко.
Слайд 4 Стереометрия. Задача 14 ЕГЭ
Задача состоит из двух
частей и оценивается в 2 балла
а) задача на доказательство
(1 балл)б) (1 балл), задачи, в основном, на:
нахождение расстояния между прямыми;
нахождение угла между прямыми;
нахождение угла между прямой и плоскостью;
нахождение угла между плоскостями;
нахождение площади сечения
Слайд 6Способы нахождения расстояния между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми равно
расстоянию между параллельными плоскостями, проходящими через эти прямые
Слайд 7Способы нахождения расстояния между скрещивающимися прямыми
Расстояние между двумя скрещивающимися прямыми
равно расстоянию от любой точки одной из них до плоскости,
проходящей через другую прямую параллельно первой прямой
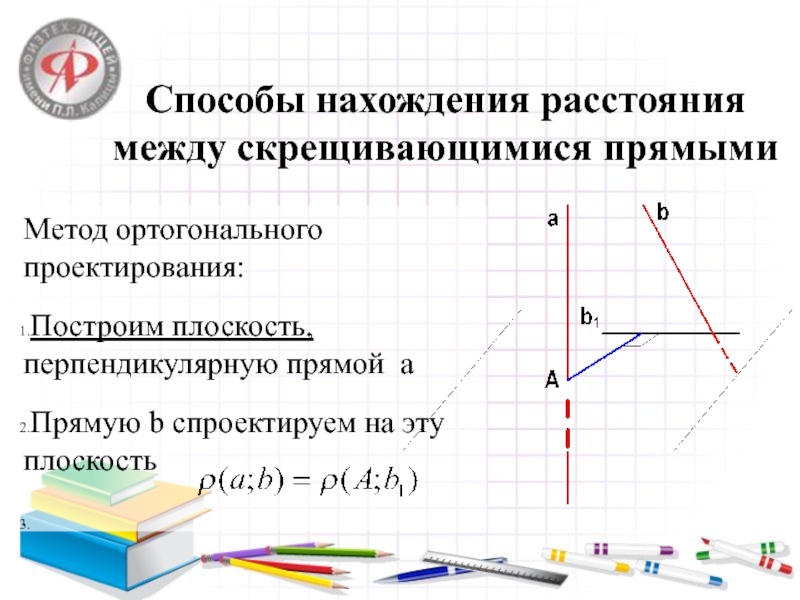
Слайд 8Способы нахождения расстояния между скрещивающимися прямыми
Метод ортогонального проектирования:
Построим плоскость,
перпендикулярную прямой a
Прямую b спроектируем на эту плоскость
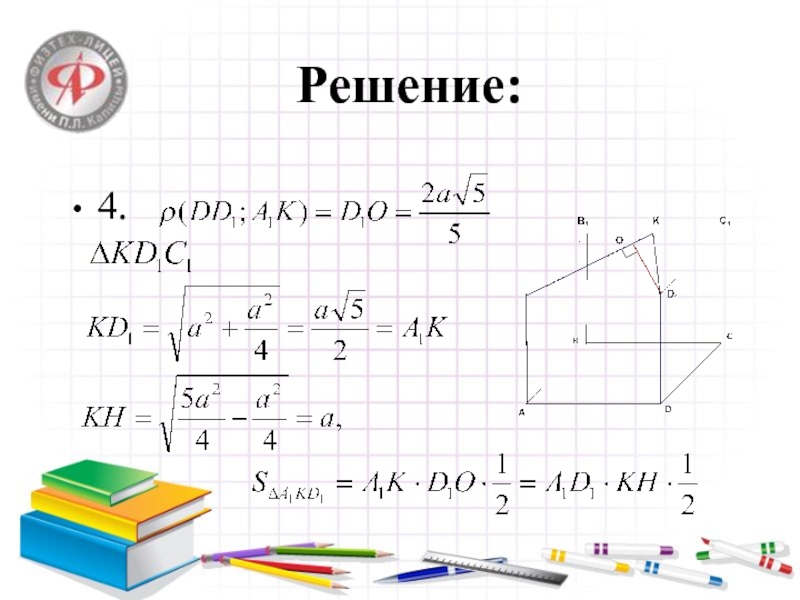
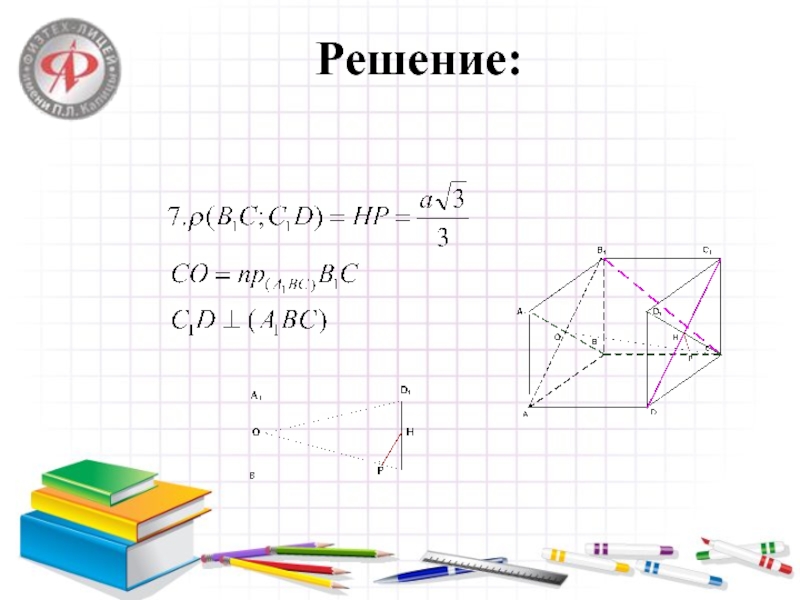
Слайд 9Задача № 4087
Дан куб
с ребром а. К-середина
ребра . Найти расстояние между прямыми:
1. 5. 9.
2. 6.
3. 7.
4. 8.
Слайд 17Технологии, используемые
в методике
1. Технология проблемного обучения
На уроке создаю проблемные
ситуации, постоянно активизирую детей на поиск рациональных способов решения задач. Учу учащихся работать самостоятельно, обобщать и конкретизировать материал. Слайд 18Технологии, используемые
в обучении
2. Интегральная технология обучения, которая предполагает слияние основных направлений
методики преподавания:укрупнение дидактических единиц;
планирование результатов обучения;
психологизация образовательного процесса
Слайд 19Технологии, используемые
в обучении
3. Использую элементы личностно-ориентированной технологии Монахова В.В.
Эта технология
предусматривает гарантированность образовательной подготовки учащихся на любом этапе учебного процесса. Говоря о личностно-ориентированной системе обучения, которую я внедряю в образовательный процесс, надо отметить два важных результата:Для ученика выстраивается четкая и рациональная система требований к его знаниям и умениям;
Я «вижу» проект будущего учебного процесса в виде системы микроцелей.
Слайд 20Задача 1
В правильной треугольной призме все ребра равны 4. Точка
M- середина ребра
а) Докажите, что прямые MB и
б)Найдите расстояние
между прямыми MB и
Слайд 23Решение
б) найти расстояние между прямыми и MB
B1C и BC1
перпендикулярны и из пункта а) имеем
BM перпендикулярна B1C, значит
B1C
перпендикулярна плоскости (MBC1) и пересекает Эту плоскость в точке O. Искомое расстояние
- это перпендикуляр PO.
Треугольник MBO подобен треугольнику
POB (первый признак подобия треугольников)
Значит
Из треугольника BCC1 BO=0,5BC1=0,5
Из треугольника MAB MB=
Из треугольника MBO MO=
OP=
Слайд 24 МЕТОД КООРДИНАТ В ЗАДАЧАХ ЕГЭ (ОСНОВНЫЕ ФОРМУЛЫ)
Расстояние между
точками A(x1; y1; z1) и В (x2; y2; z2) (как
и модуль вектора ) в прямоугольной декартовой системе координат Oxyz находится по формуле2. Скалярным произведением векторов (x1; y1; z1) и (x2; y2; z2) называется число
3. Если (x1; y1; z1) и (x2; y2; z2) – ненулевые вектора, а α – угол между ними, то
Слайд 25 МЕТОД КООРДИНАТ В ЗАДАЧАХ ЕГЭ (ОСНОВНЫЕ ФОРМУЛЫ)
4. Векторы
(x1; y1; z1) и (x2; y2; z2) перпендикулярны (ортогональны) тогда
и только тогда, когда или .5. Уравнение плоскости, проходящей через точку M0(x0; y0; z0) перпендикулярно ненулевому вектору (A; B; C) – вектору нормали плоскости, имеет вид
, или A(x-x0)+B(y-y0)+(C(z-z0)=0.
6. Любое уравнение Ax+By+Cz+D=0, где числа A, B, C одновременно не равны 0, есть уравнение некоторой плоскости, причем (A; B; C) – вектор нормали этой плоскости.
Слайд 26 МЕТОД КРДИНАТ В ЗАДАЧАХ ЕГЭ (ОСНОВНЫЕ ФОРМУЛЫ)
7.
Косинус угла между плоскостями равен модулю косинуса угла между векторами
нормалей этих плоскостей, то есть, если β – угол между плоскостями, заданными уравнениями A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, то8. Расстояние d от точки M0(x0; y0; z0) до плоскости, заданной уравнением Ax+By+Cz+D=0, находится по формуле
9. Если – угол между прямой с направляющим вектором и плоскостью
Ax+By+Cz+D=0 c вектором нормали то равен модулю косинуса угла между этими векторами, то есть
Слайд 27Задача 2
В единичном кубе ABCDA1 B1C1D1 найдите угол между прямымиAB1
и BC1.
Впишем куб в систему координат как показано на рисунке
Найдем
координаты концов отрезков
Слайд 28Задача 3
Дана правильная четырехугольная призма ABCDA1B1C1D1 со стороной
основания и
боковым ребром 2. Точки M и N – середины ребер
A1B1 и CC1 соответственно.а) Докажите, что MN перпендикулярно BC1
б) Найдите расстояние от точки M до плоскости (BC1D)
а) Введем систему координат.
-1);
Значит, MN перпендикулярно BC1
б) D(
Уравнение плоскости (BC1D):
Расстояние от точки M до плоскости (BC1D): (BC1D))=
Слайд 29Площадь ортогональной проекции многоугольника
Площадь ортогональной проекции многоугольника на плоскость равна
площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника
и плоскости проекции, то есть
Слайд 30Задача 4
В правильной треугольной призме, каждое ребро которой равно 9
дм, постройте сечение, проходящее через сторону основания и середину отрезка,
соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сеченияа) Из треугольника ABK OK= =
Из треугольника OEK
Значит
б) Треугольник равен треугольнику . Значит
То есть
Имеем . Значит 36
Слайд 31Краткое описание методики
Настоящая методика основана на реализации принципов профильного обучения
– региональности, вариативности, индивидуализации и дифференциации обучения;
Изучение тем программы с
позиций курса высшей математики; Реализация прикладной направленности обучения математике с использованием ИКТ