Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описанная и вписанная окружности треугольника
Содержание
- 1. Описанная и вписанная окружности треугольника
- 2. Тема урока: Описанная и вписанная окружности треугольника
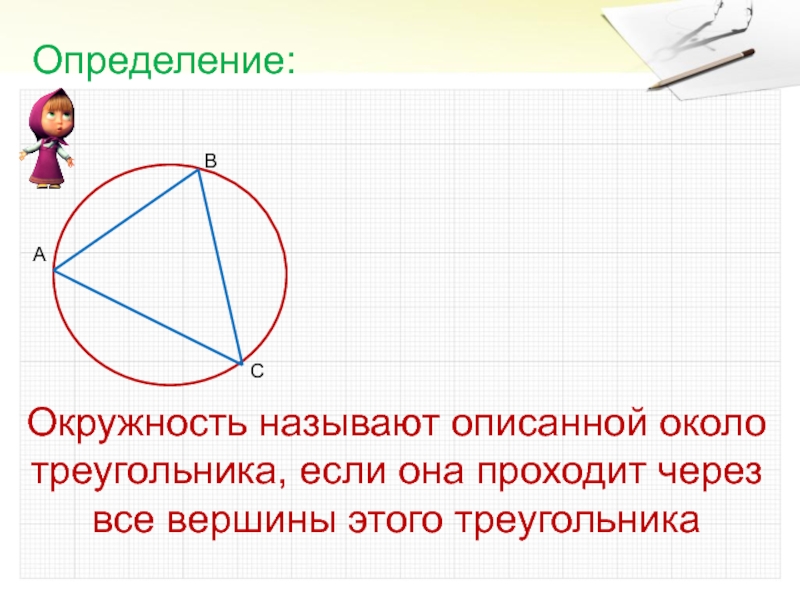
- 3. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника Определение:
- 4. На каком рисунке окружность описана около треугольника:12345Если окружность описана около треугольника, то треугольник вписан в окружность.
- 5. Около любого треугольника можно описать окружностьЗаметим, около
- 6. Окружность называют вписанной в треугольник, если она касается всех его сторонОпределение:
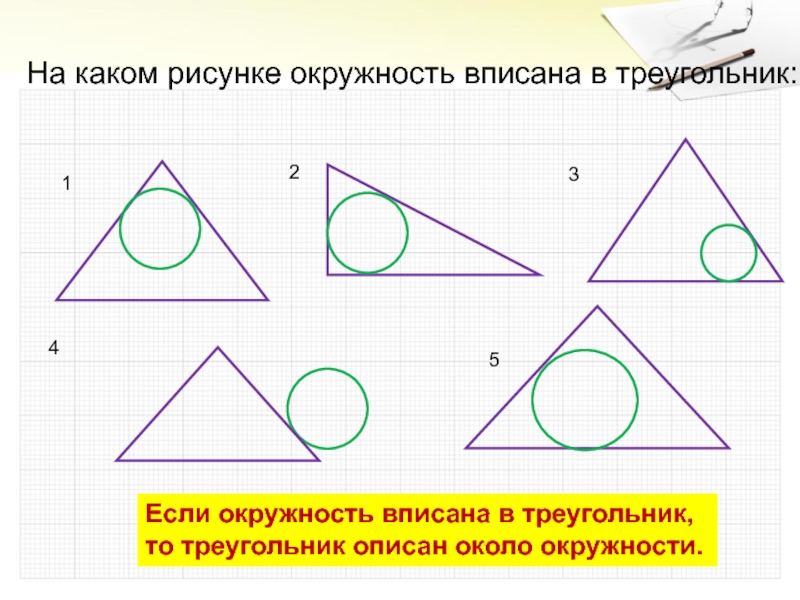
- 7. На каком рисунке окружность вписана в треугольник:134Если окружность вписана в треугольник, то треугольник описан около окружности.25
- 8. Заметим, в треугольник можно вписать окружность,
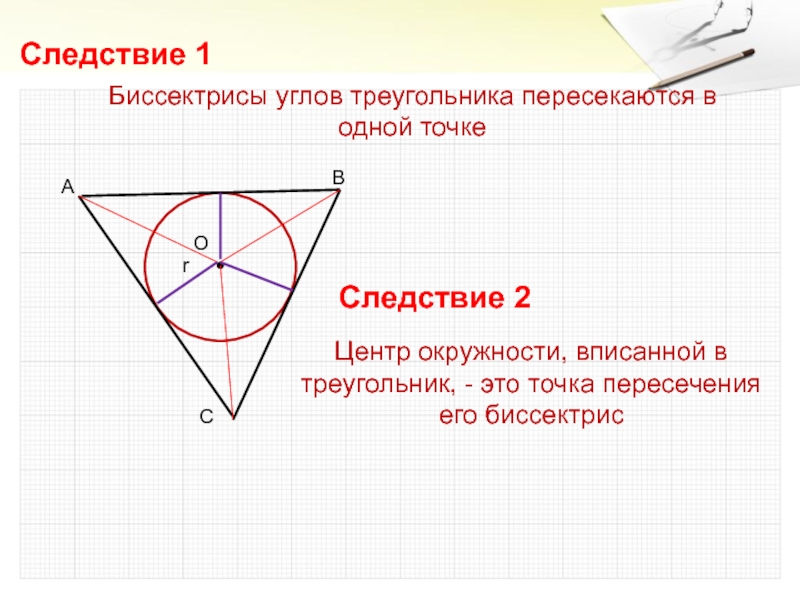
- 9. rБиссектрисы углов треугольника пересекаются в одной точкеСледствие
- 10. Радиус окружности вписанной в прямоугольный треугольник, определяется
- 11. Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану, проведенную к его основанию.О
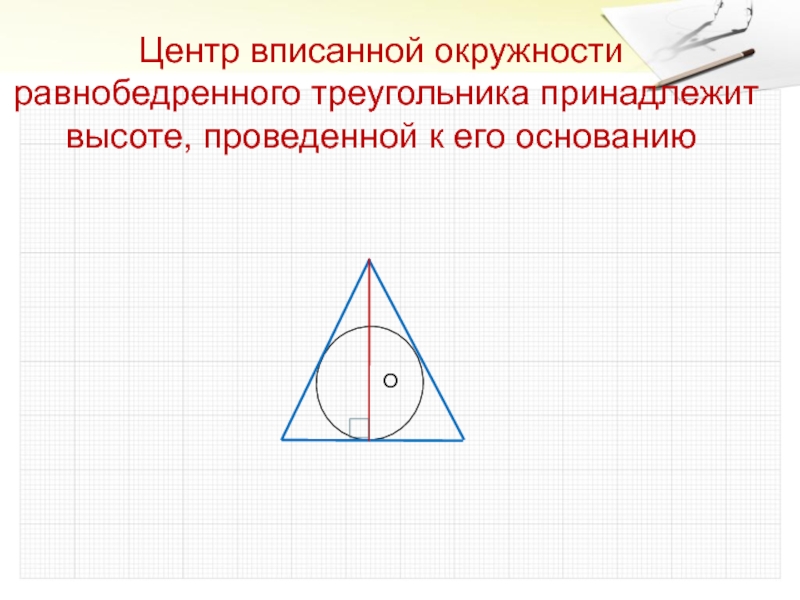
- 12. Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его основаниюО
- 13. Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.
- 14. Если центр окружности, описанной около треугольника принадлежит его стороне, то треугольник - прямоугольный
- 15. № 550, 552, 557540, 542Учебник
- 16. Ответьте на вопрос. Мне было интересно узнать о…Легче всего мне было…Трудности вызвало…
- 17. § 21 учить ,№ 553,558Домашнее задание
- 18. 1. Геометрия 7 классы Мерзляк А.Г., М. «Вентана-Граф»2. Анимация http://animashky.ru/index/0-11?25-63. Шаблон http://office.microsoft.com/ru-ru/templates/CT010142747.aspx#ai:TC010362639|Литература и источники
- 19. Скачать презентанцию
Тема урока: Описанная и вписанная окружности треугольника
Слайды и текст этой презентации
Слайд 3
Окружность называют описанной около треугольника, если она проходит через все
вершины этого треугольника
Слайд 4На каком рисунке окружность описана около треугольника:
1
2
3
4
5
Если окружность описана около
треугольника,
то треугольник вписан в окружность.
Слайд 5Около любого треугольника можно описать окружность
Заметим, около треугольника можно описать
только одну окружность
Теорема 21.1
Три серединных перпендикуляра сторон треугольника пересекаются в
одной точкеСледствие 1
Следствие 2
Центр окружности, описанной около треугольника, - это точка пересечения серединных перпендикуляров его сторон
Слайд 7
На каком рисунке окружность вписана в треугольник:
1
3
4
Если окружность вписана в
треугольник,
то треугольник описан около окружности.
2
5
Слайд 8Заметим, в треугольник можно вписать окружность,
и притом только одну.
О
С1
А1
В1
В любой треугольник можно
вписать окружностьТеорема 21.2
Слайд 9r
Биссектрисы углов треугольника пересекаются в одной точке
Следствие 1
Следствие 2
Центр окружности,
вписанной в треугольник, - это точка пересечения его биссектрис
Слайд 10Радиус окружности вписанной в прямоугольный треугольник, определяется по формуле
где
r – радиус вписанной окружности,
а и b - катеты,
c - гипотенуза
Слайд 11Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану,
проведенную к его основанию.
О
Слайд 12Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его
основанию
О
Слайд 13Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.
Слайд 14Если центр окружности, описанной около треугольника принадлежит его стороне, то
треугольник - прямоугольный
Слайд 181. Геометрия 7 классы Мерзляк А.Г., М. «Вентана-Граф»
2. Анимация http://animashky.ru/index/0-11?25-6
3.
Шаблон http://office.microsoft.com/ru-ru/templates/CT010142747.aspx#ai:TC010362639|
Литература и источники
