Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Призма. Площадь поверхности призмы 10 класс
Содержание
- 1. Призма. Площадь поверхности призмы 10 класс
- 2. «Геометрия является самым могущественным средством
- 3. Геометрическая зарядка Ребро куба равно 4 см.Найти
- 4. Проверяем и оцениваемПлощади фигур6,12—8 кв. см6,13—10кв.см6,14—12кв.см6,15—6кв.смПлощади поверхностиКуба—96кв.смПравильной шестиугольной призмы-300кв.см
- 5. Проверяем изученноеОпределение призмы, ее элементы. Виды призм Площадь боковой поверхности призмы. Задачи № 229 (а)
- 6. ПризмаА1А2АnB1B2BnB3А3Многогранник, составленный из двух равных многоугольников А1А2…Аn
- 7. Если боковые ребра перпендикулярны к основаниям, то
- 8. Прямая призма называется правильной, если ее основания
- 9. Площадью полной поверхности призмы называется сумма площадей
- 10. Задача № 229(а)Дано: АВСА1В1С1-правильная треугольная призма.АВ=10 см.
- 11. Самостоятельная работаЗадача №1: сторона основания правильной треугольной
- 12. План решения задачи. 1.Внимательно прочитать задачу. Помни,
- 13. Слайд 13
- 14. Скачать презентанцию
«Геометрия является самым могущественным средством для измерения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.»
Слайды и текст этой презентации
Слайд 1Решение задач по теме
«Призма. Площадь поверхности призмы»
10 класс
«Берновская СОШ»
Учитель Земцова
М.В.
Слайд 2 «Геометрия является самым могущественным средством для измерения наших
умственных способностей и дает нам возможность правильно мыслить и рассуждать.»
Галилео Галилей Слайд 3Геометрическая зарядка
Ребро куба равно 4 см.
Найти его площадь поверхности
Найти
площадь боковой поверхно-
сти правильной шестиугольной
призмы, сторона основания
которой равна
5 см, а высота 10см. Слайд 4Проверяем и оцениваем
Площади фигур
6,12—8 кв. см
6,13—10кв.см
6,14—12кв.см
6,15—6кв.см
Площади поверхности
Куба—96кв.см
Правильной шестиугольной призмы-300кв.см
Слайд 5Проверяем изученное
Определение призмы, ее элементы. Виды призм
Площадь боковой поверхности
призмы.
Задачи № 229 (а)
Слайд 6Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных
в параллельных плоскостях, и n параллелограммов, называется призмой.
n-угольная призма.
Многоугольники
А1А2…Аn
и В1В2…Вn – основания призмы.Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
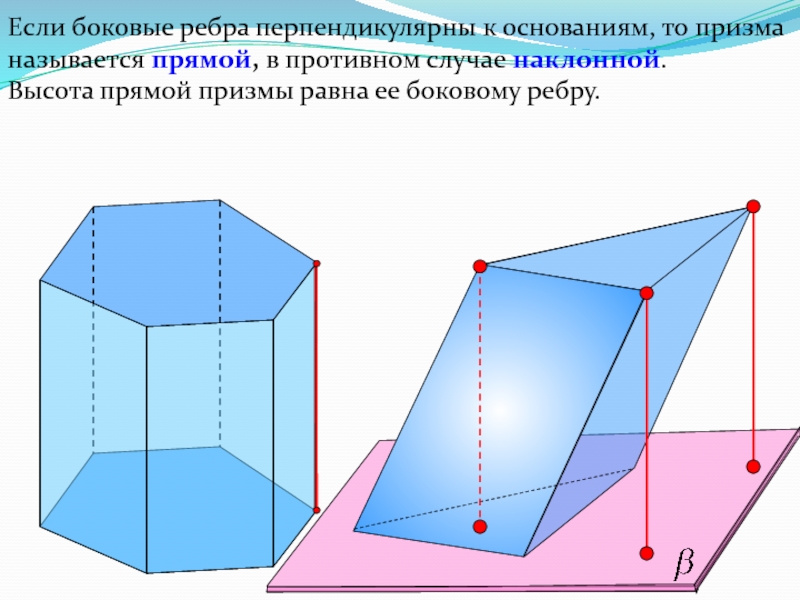
Слайд 7Если боковые ребра перпендикулярны к основаниям, то призма называется прямой,
в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.
Слайд 8Прямая призма называется правильной, если ее основания - правильные многоугольники.
У такой призмы все боковые грани – равные прямоугольники.
Слайд 9Площадью полной поверхности призмы называется сумма площадей всех граней, а
площадью боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
Pocн
Слайд 10Задача № 229(а)
Дано: АВСА1В1С1-правильная
треугольная призма.
АВ=10 см. АА1=15 см.
Найти:S,бок,
; Sпов.
Решение
Sбок = Рh Р=10·3=30 (см.) h=15см. Sбок=30·15=450
(см2)Sпов = Sбок+2 Sосн. Sосн.= . Sосн=100/4=25(см2)
Sпов=450+25(см2)
Ответ: 450+25(см2)
Слайд 11Самостоятельная работа
Задача №1: сторона основания правильной треугольной призмы равна 6см.,
а диагональ боковой грани равна 10см. Найти площадь боковой и
полной поверхности призмы.Проверка: Росн.=3·6=18 (см2) Sбок = Рh Sбок=18·8=144(см2) Sосн.= . Sосн=62/4=9см2
h= =8(см.) Sпов = Sбок+2 Sосн. Sпов=144+2·9=144+18(см2) Ответ: 144+18(см2)
Слайд 12План решения задачи.
1.Внимательно прочитать задачу. Помни, каждое слово задачи несет
информацию, необходимую для ее решения.
2. Выполни рисунок к задаче и
отметь на нем все, что известно.3.Запиши что дано и что надо найти
4.Сделай обоснование рисунка, если нужно.
5.Начинай решение с ответа на главный вопрос задачи.
6.Запиши нужную формулу или выдели треугольник, в который входит неизвестное.
7.Запиши все, что известно (в этой формуле) об этом треугольнике и если достаточно данных найди неизвестное, пользуясь правилами решения прямоугольных треугольников (теорема Пифагора, значение синуса, косинуса, тангенса острого угла и т.д.) или просто треугольников (например: теорема синусов, теорема косинусов и т.д.) Задача решена.
8.В противном случае у тебя появится новое неизвестное, которое необходимо найти, рассматривая уже другой треугольник.
9.И так до тех пор, пока рассматриваемый треугольник не будет решен.
10.Найди ответ на главный вопрос задачи, для этого вернись к первому, рассматриваемому тобой треугольнику п.6 и реши его.
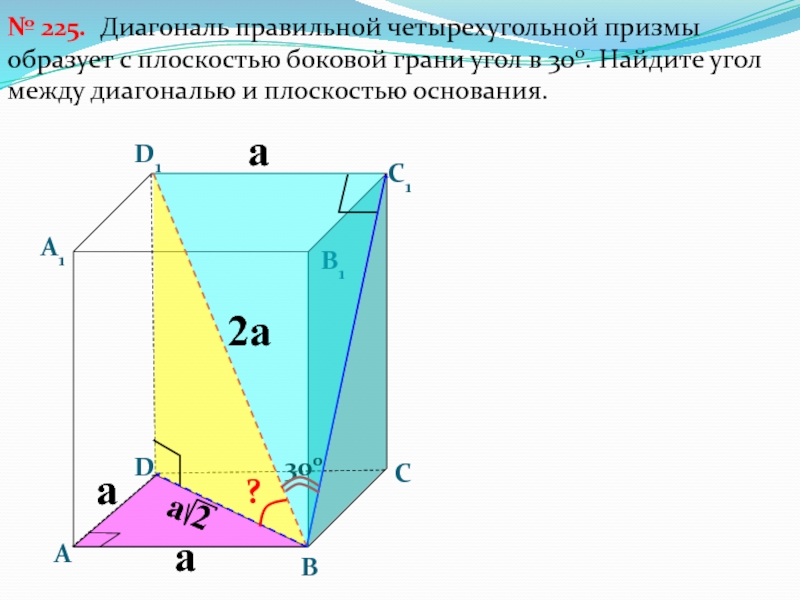
Слайд 13 Диагональ правильной четырехугольной
призмы образует с плоскостью боковой грани угол в 300. Найдите
угол между диагональю и плоскостью основания.№ 225.
В
С
А1
D1
С1
В1
D
А
a
2a