Разделы презентаций

Золотое сечение в геометрии

Содержание

Правило Золотого Сечения впервые сформулировано Евклидом. Вкратце оно определяется так: отношение целого к большей части должно равняться отношению большей части к меньшей. Таким образом, по Платону, достигается ощущение "наиболее совершенного единого

Слайды и текст этой презентации

Слайд 1Золотое сечение в геометрии

Золотое сечение в геометрии

Слайд 2Правило Золотого Сечения впервые сформулировано Евклидом. Вкратце оно определяется так:

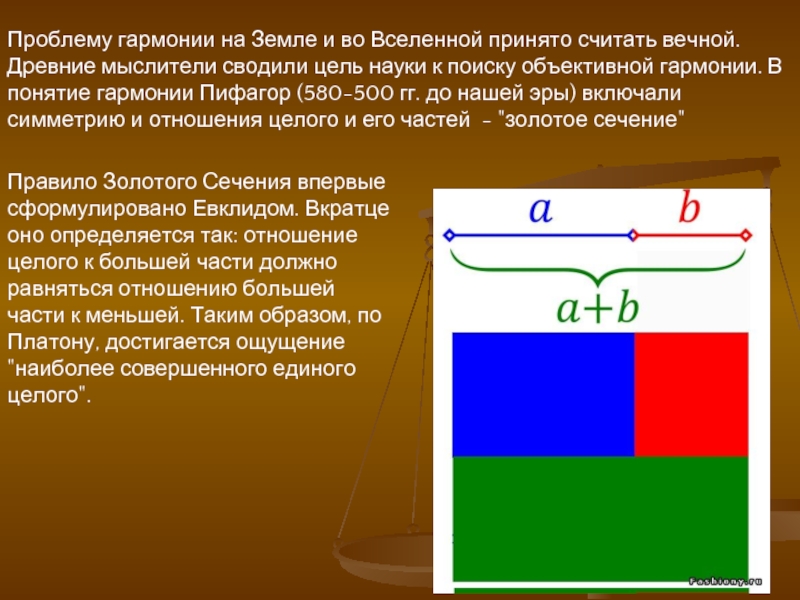
отношение целого к большей части должно равняться отношению большей части

к меньшей. Таким образом, по Платону, достигается ощущение "наиболее совершенного единого целого".

Проблему гармонии на Земле и во Вселенной принято считать вечной. Древние мыслители сводили цель науки к поиску объективной гармонии. В понятие гармонии Пифагор (580-500 гг. до нашей эры) включали симметрию и отношения целого и его частей - "золотое сечение"

Правило Золотого Сечения впервые сформулировано Евклидом. Вкратце оно определяется так: отношение целого к большей части должно равняться

Слайд 3Важно отметить два вида проявлений Золотого Сечения в живой природе: 1.

иррациональные отношения по Пифагору - 1.62 2. целочисленные, дискретные -

по Фибоначчи.
Важно отметить два вида проявлений Золотого Сечения в живой природе: 1. иррациональные отношения по Пифагору - 1.62

Слайд 4Одна из задач Фибоначчи гласила «Сколько пар кроликов в один

год от одной пары родится». Размышляя на эту тему, Фибоначчи

выстроил такой ряд цифр:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Для того, чтобы получить каждое следующее число в этом ряду, надо сложить два предыдущих: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и так далее. 

Одна из задач Фибоначчи гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на

Слайд 5Пифагор был первым, кто обратил внимание на особое «гармоничное» деление

любого отрезка, позднее названное «золотым сечением».
Приближенные значения таковы: 1,61803398875

Пифагор был первым, кто обратил внимание на особое «гармоничное» деление любого отрезка, позднее названное «золотым сечением».Приближенные значения

Слайд 6Пропорции различных частей нашего тела составляют число, очень близкое к

золотому сечению. Если эти пропорции совпадают с формулой золотого сечения,

то внешность или тело человека считается идеально сложенными. Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.

Золотое сечение и тело человека

Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с

Слайд 7Изучая конструкции раковин, ученые обратили внимание на то, что форма

раковин поражает своим совершенством и экономичностью средств, затраченных на ее

создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, "отточенной" конструкции  У большинства улиток, которые обладают раковинами, раковина растет в форме спирали, которая точно соответствует "золотой пропорции"

Золотое сечение в природе

Изучая конструкции раковин, ученые обратили внимание на то, что форма раковин поражает своим совершенством и экономичностью средств,

Слайд 8Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов

микроскопически малы, так что мы не можем разглядеть их невооруженным

глазом.  Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. 

Золотое сечение и кристаллы

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем

Слайд 9Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена

на "золотых треугольниках».  Таким образом, Леонардо Да Винчи использовал в своей

картине не только принцип симметрии, но и Золотое сечение

Золотое сечение в искусстве

Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена на

Слайд 10Интересные сведения о периодах жизни человека, связанные с числами Фибоначчи.

Критические возрасты мужчин соответствуют следующим годам: 1, 2, 3, 5,

8, 13, 21, 34, 55, 89,… Периодичность в жизни женщины подчиняется ряду Люка: 1, 3, 4, 7, 11, 18, 29, 47, 76, 123. Сдвижка возрастных интервалов объясняется более ранним развитием девочек.

Золотое сечение и возраст человека

Интересные сведения о периодах жизни человека, связанные с числами Фибоначчи. Критические возрасты мужчин соответствуют следующим годам:

Слайд 11В фотографии используется упрощенный вариант построения «Золотого сечения» или правило

«Трети». Заключается оно в следующем: мы мысленно делим кадр на

три части по горизонтали и вертикали и, в точках пересечения воображаемых линий, размещаем ключевые детали снимаемой сцены.

Золотое сечение в фотографии

В фотографии используется упрощенный вариант построения «Золотого сечения» или правило «Трети». Заключается оно в следующем: мы мысленно

Слайд 12Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое

сечение. Его талант был многогранным, но в большей степени он

проявился в многочисленных проектах жилых домов и усадеб. Например, золотое сечение можно встретить в архитектуре здания бывшего сената в Кремле, Дворца в Петровском Алабине и Голицынской больницы в Москве

Золотое сечение в архитектуре

Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но в

Слайд 13С помощью правильных пропорций можно получать гармоничные образы, скорректировать недостатки

фигуры, а это важно в профессии закройщика.
Золотое сечение в одежде

С помощью правильных пропорций можно получать гармоничные образы, скорректировать недостатки фигуры, а это важно в профессии закройщика.Золотое

Слайд 14Таким образом всё в нашем мире без исключения подчиняется закону

золотого сечения и это всегда было есть и будет.

Таким образом всё в нашем мире без исключения подчиняется закону золотого сечения и это всегда было есть
Теги

Похожие презентации

Лист Мёбиуса Лист Мёбиуса 559
Проект : «пирамида» Проект : «пирамида» 494
Графический способ решения систем укравнений Графический способ решения систем укравнений 406
Стереометрия в образах Стереометрия в образах 431
Площади фигур. Теорема Пифагора Площади фигур. Теорема Пифагора 404
Площадь трапеции Площадь трапеции 469
Симметрия и осевая симметрия Симметрия и осевая симметрия 560
Задачи на построение сечений Задачи на построение сечений 786
Измерение отрезков и углов (тест) 7 класс Измерение отрезков и углов (тест) 7 класс 396
Построение сечений пирамиды (тетраэдра) Построение сечений пирамиды (тетраэдра) 978
Прямоугольный треугольник в древнем Египте и в современной геометрии Прямоугольный треугольник в древнем Египте и в современной геометрии 411
Прямоугольный треугольник. Решение задач 7 класс Прямоугольный треугольник. Решение задач 7 класс 486
Параллельность прямых и плоскостей Параллельность прямых и плоскостей 381
Углы, связанные с окружностью Углы, связанные с окружностью 326
Свойства пирамиды с равными боковыми ребрами Свойства пирамиды с равными боковыми ребрами 566
Геометрические фигуры в пространстве Геометрические фигуры в пространстве 829
Задачи на построение 7 класс Задачи на построение 7 класс 416
Мир систем координат Мир систем координат 526
Круг и окружность Круг и окружность 352
Теорема о сумме углов треугольника 7 класс Теорема о сумме углов треугольника 7 класс 392

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика