Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Вариньона и ее применение 9 класс
Содержание
- 1. Теорема Вариньона и ее применение 9 класс
- 2. Теорема Вариньона: Фигура, образованная путем
- 3. Применение теоремы Вариньона к доказательству некоторых утвержденийУтверждение
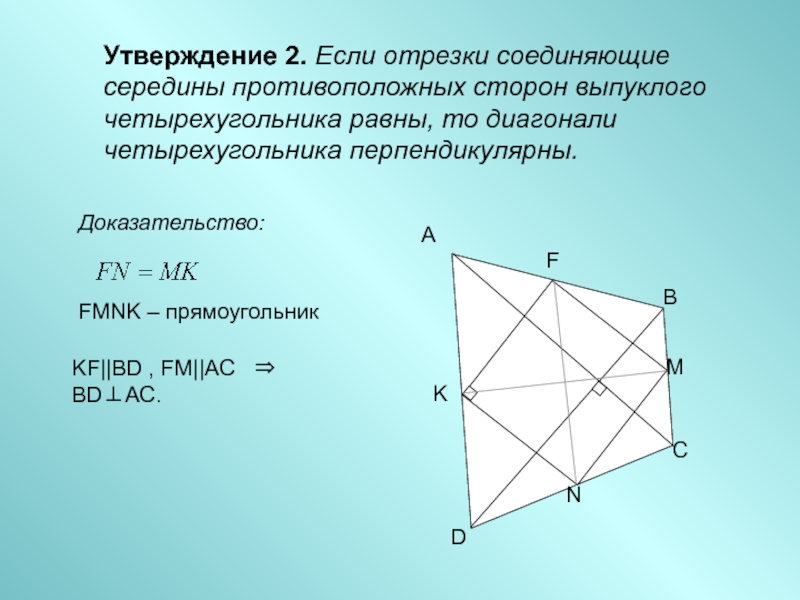
- 4. Утверждение 2. Если отрезки соединяющие середины противоположных
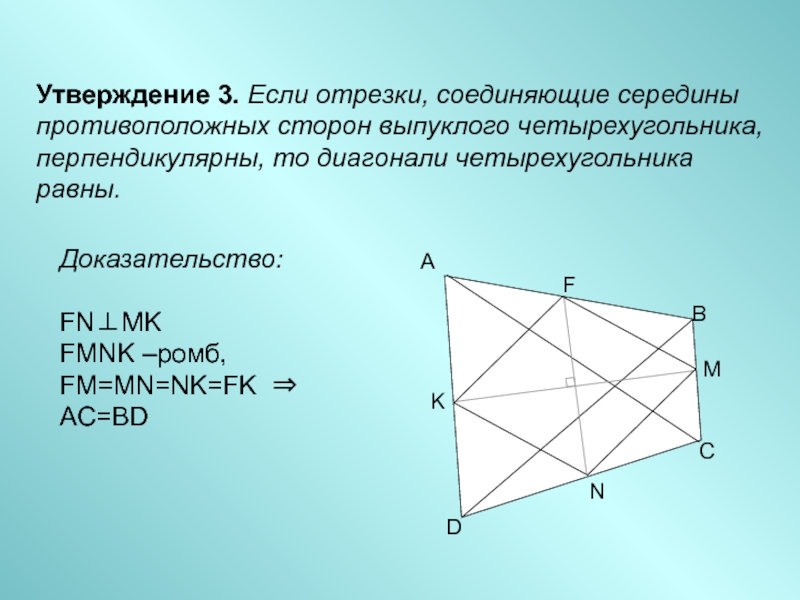
- 5. Утверждение 3. Если отрезки, соединяющие середины противоположных
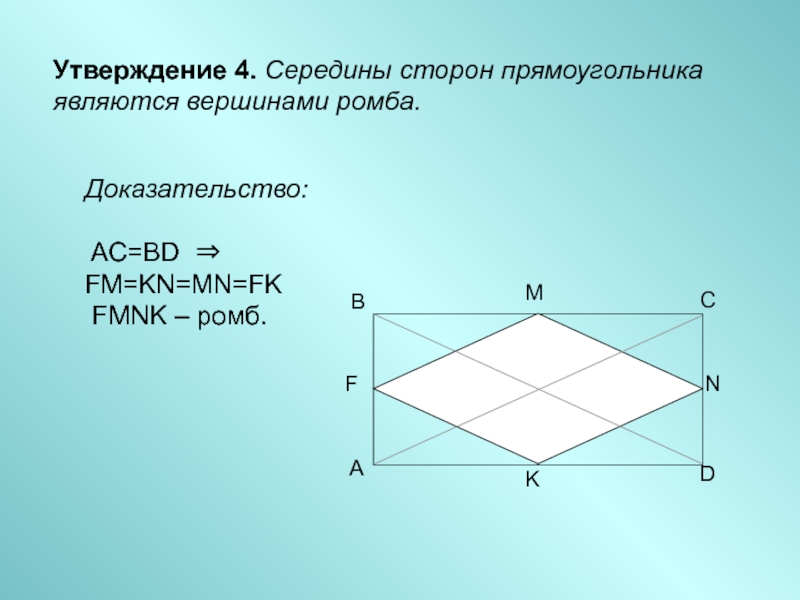
- 6. Утверждение 4. Середины сторон прямоугольника являются вершинами ромба.Доказательство: AC=BD ⇒ FM=KN=MN=FK FMNK – ромб.
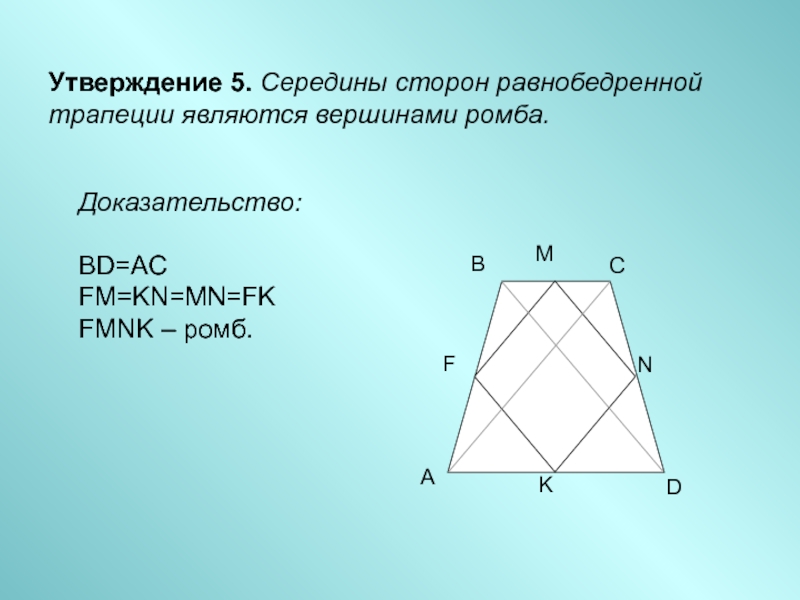
- 7. Утверждение 5. Середины сторон равнобедренной трапеции являются вершинами ромба.Доказательство: BD=AC FM=KN=MN=FK FMNK – ромб.
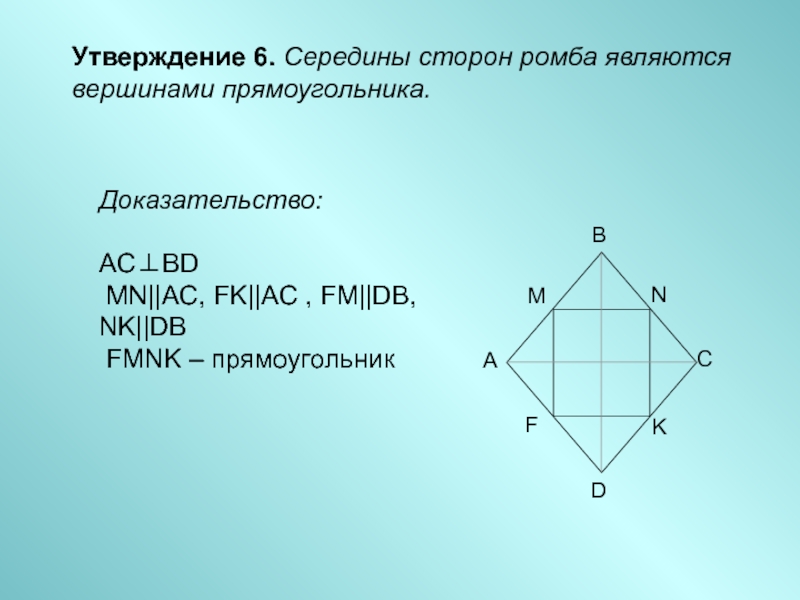
- 8. Утверждение 6. Середины сторон ромба являются вершинами
- 9. Скачать презентанцию
Теорема Вариньона: Фигура, образованная путем последовательного соединения середин сторон четырехугольника, является параллелограммом, а его площадь равна половине площади данного четырехугольника.
Слайды и текст этой презентации
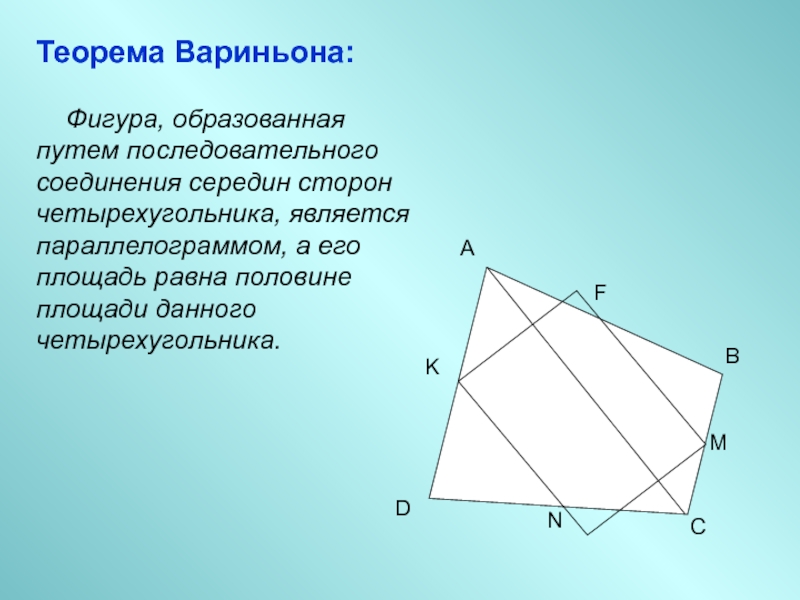
Слайд 2Теорема Вариньона:
Фигура, образованная путем последовательного соединения середин
сторон четырехугольника, является параллелограммом, а его площадь равна половине площади
данного четырехугольника.Слайд 3Применение теоремы Вариньона к доказательству некоторых утверждений
Утверждение 1. В выпуклом
четырехугольнике сумма квадратов диагоналей в 2 раза больше суммы квадратов
отрезков соединяющих середины противоположных сторон.Доказательство: