Построение сечений в многогранниках методом следов 10 класс

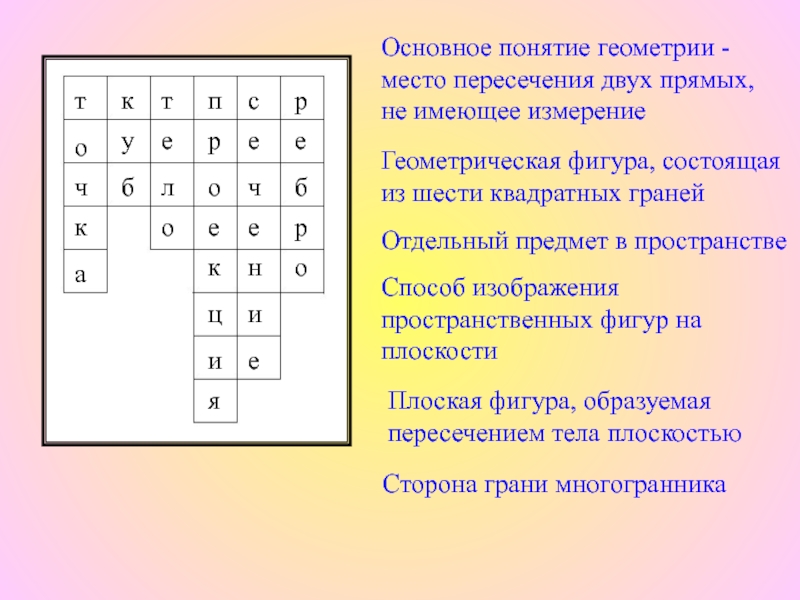
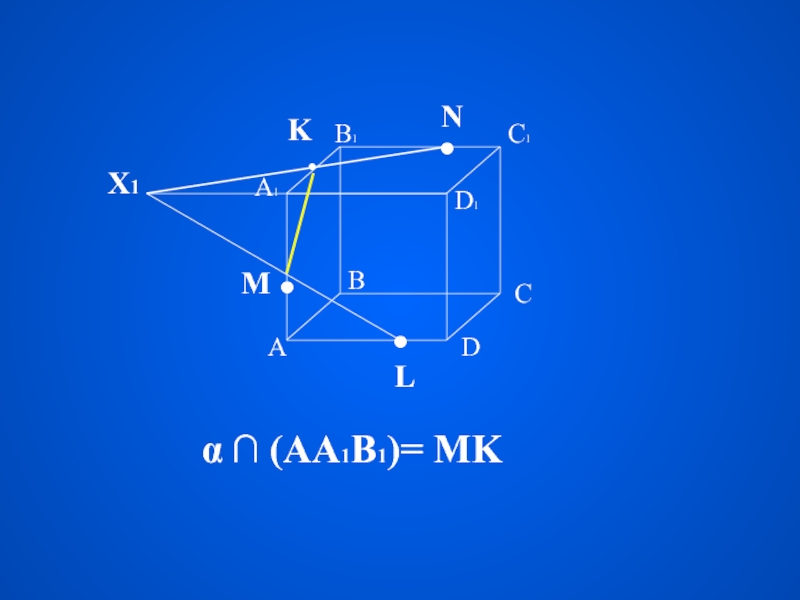
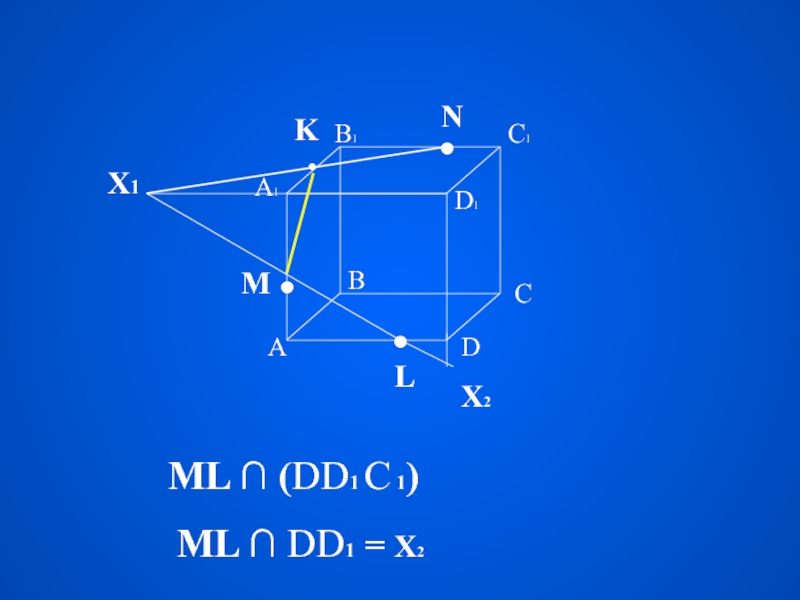
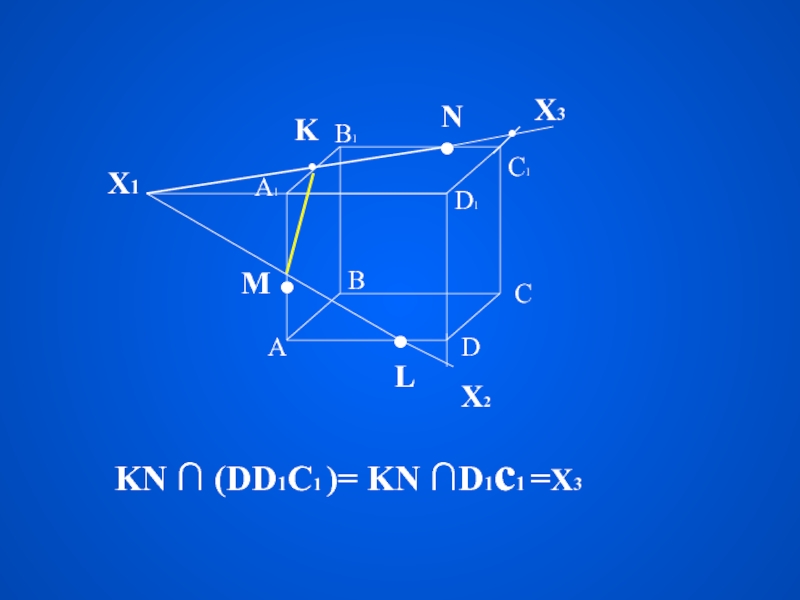
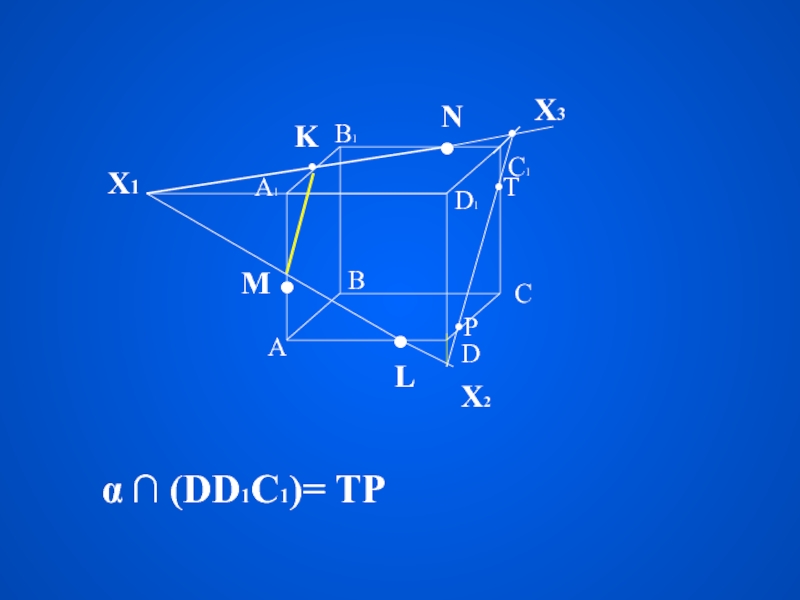
измерение

т
о
ч
к
а
Геометрическая фигура, состоящая из шести квадратных граней

к
у
б
Отдельный предмет в пространстве

т
е
л
о
Способ

п

р

о

е

к

ц

и

я

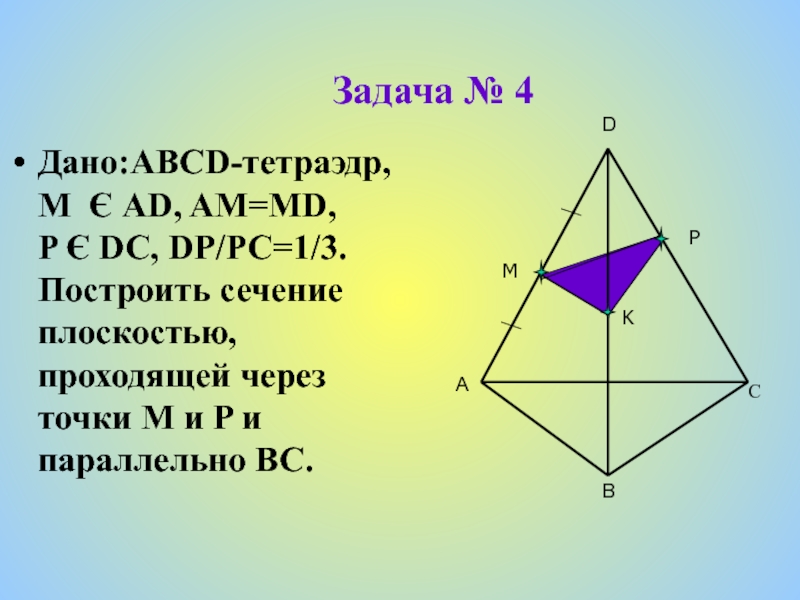
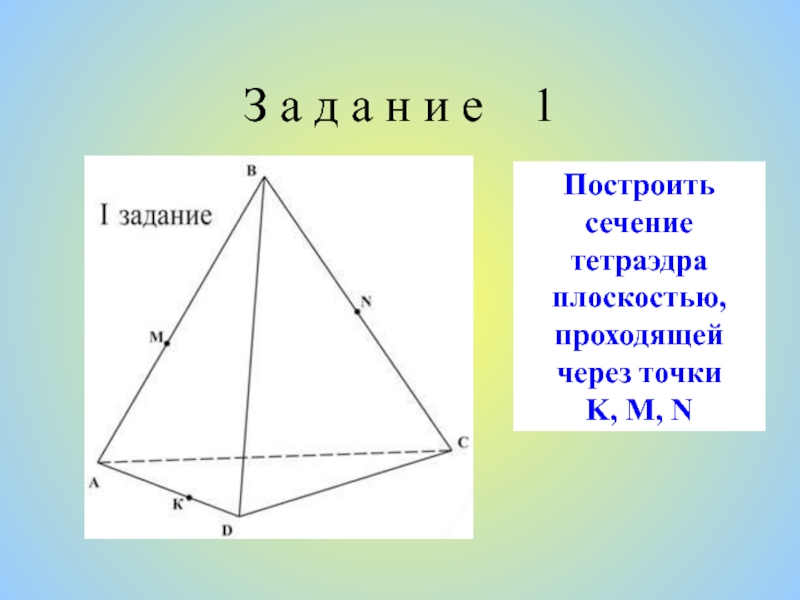
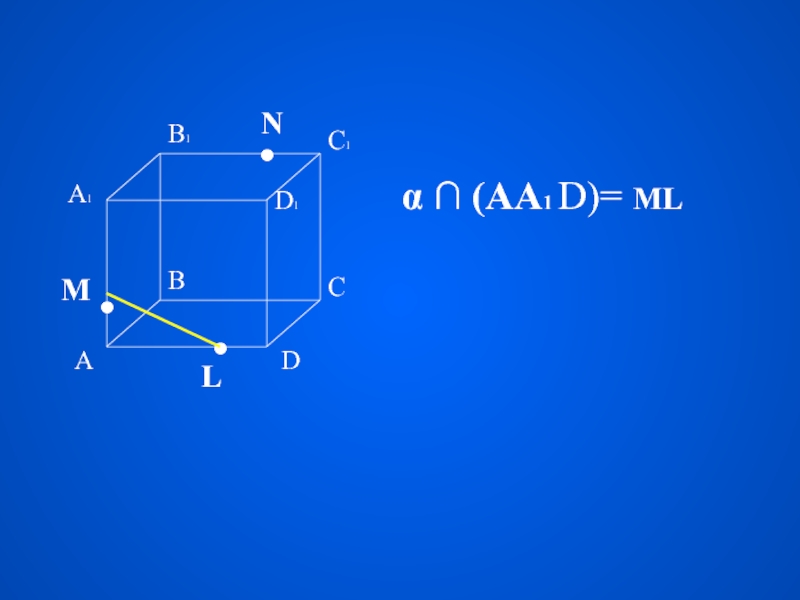
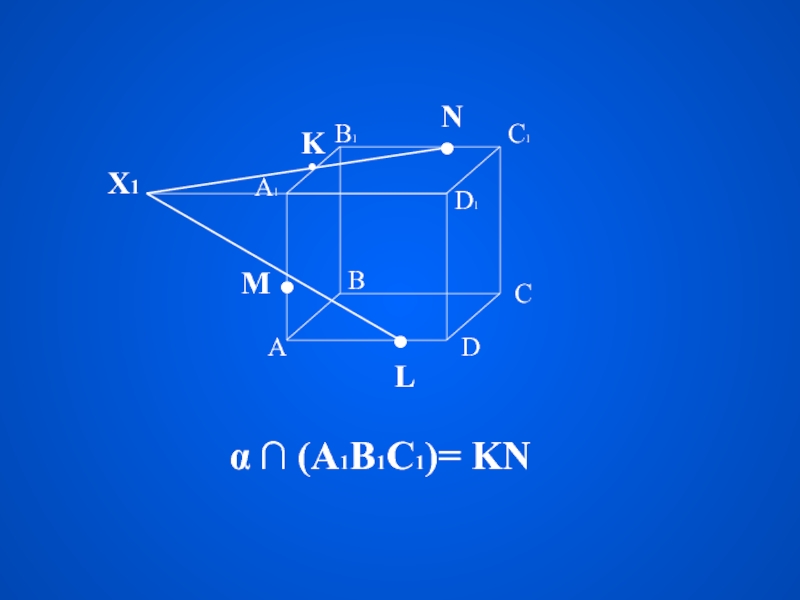
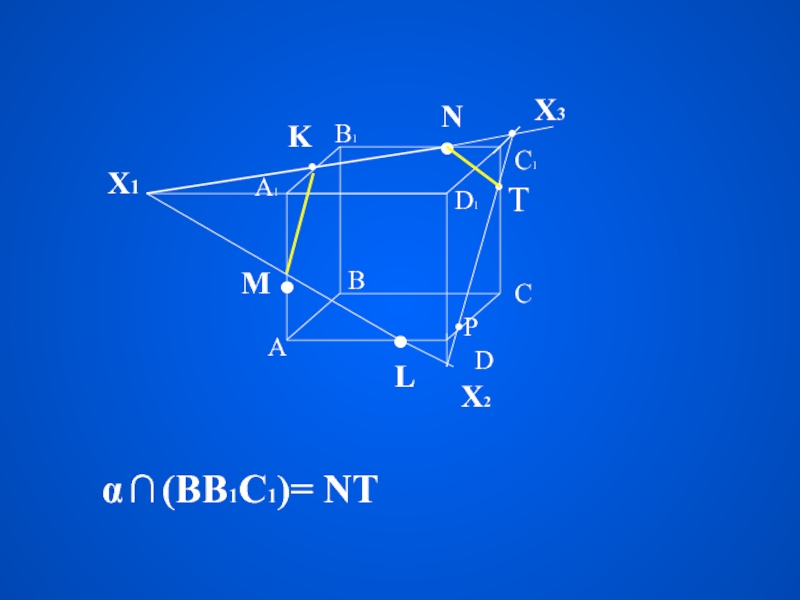
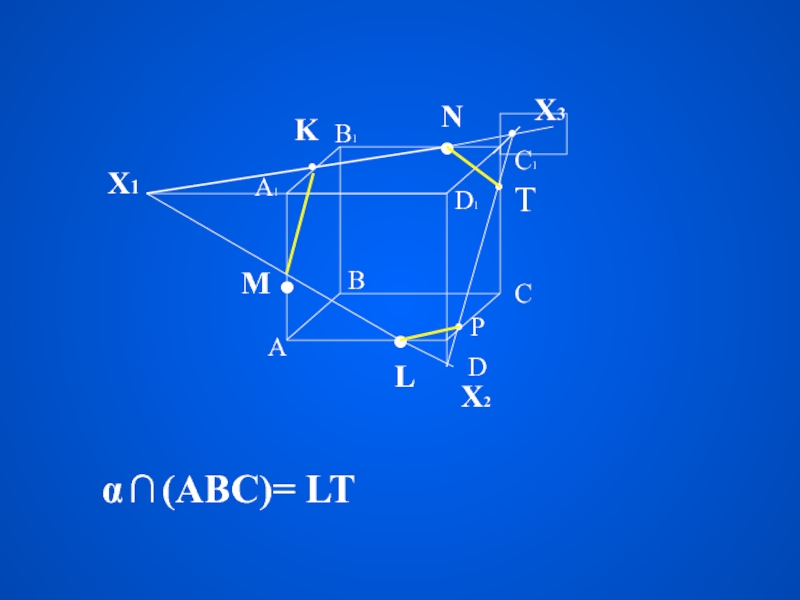
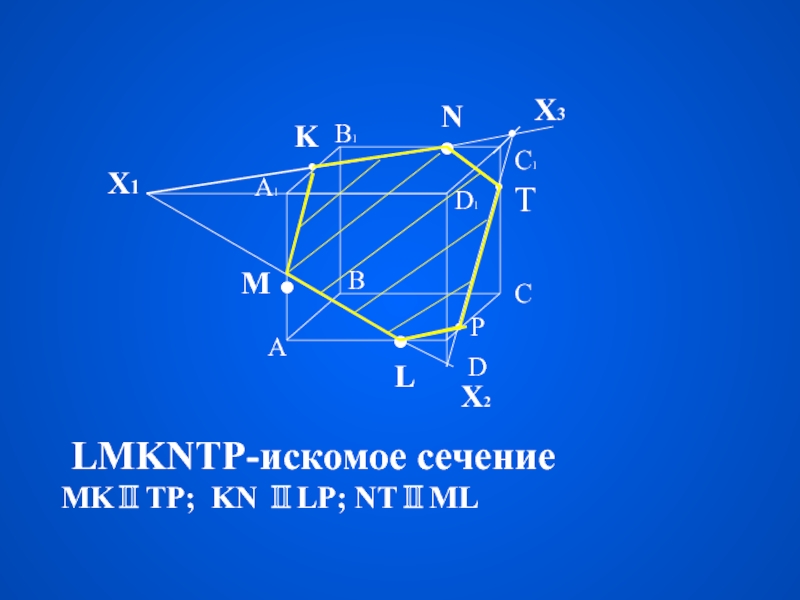
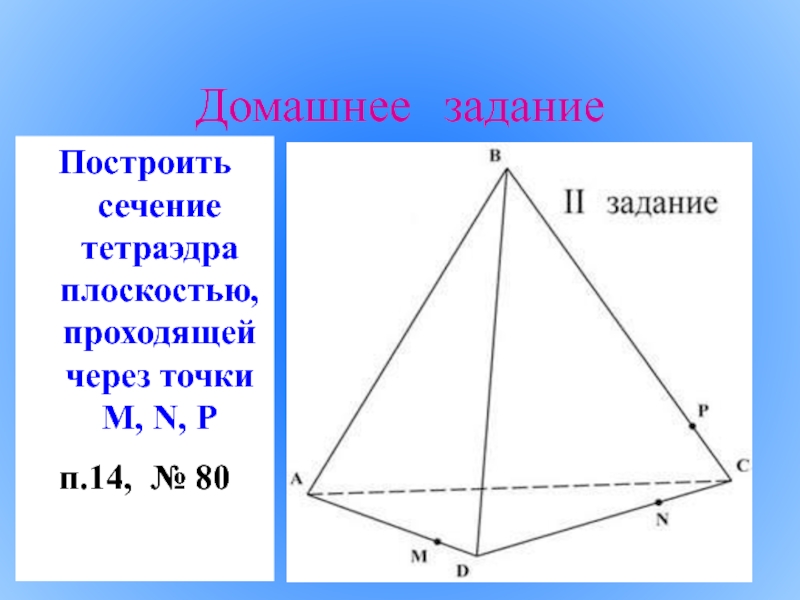
Плоская фигура, образуемая пересечением тела плоскостью

с

е

ч

е

н

и

е

Сторона грани многогранника

р

е

б

р

о

в многогранниках методом следов.
17 ноября. 2009г.

рассечении тела плоскостью.

Что называется сечением?

в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.
С е

точки пересечения прямой с плоскостью, построение линии пересечения двух плоскостей,

Построение сечений

секущей плоскости с плоскостью основания многогранника.
Находим точки пересечения секущей

Метод следов

Куб, тетраэдр, четырёхугольная пирамида, призма являются примерами многогранников.



О с н

ADC. Построить сечение данного тетраэдра через точки N, P, B.




B
A
C
D
N
P

P Є CD, F Є BC. Построить сечение, проходящее через

A

B

C

D

M

N

P

K

F

N Є ACD. Построить сечение MNK.



A
B
C
D



K


P
L
H
F
М

N

Є DC, DP/PC=1/3. Построить сечение плоскостью, проходящей через точки M

A

B

D

M

P

K

С

тетраэдра плоскостью, проходящей через точки K, M,

через заданные точки N, C, D1.

N L) = α

Х2

Х2

MKⅡTP; KN ⅡLP; NTⅡML


•
T
• P

тетраэдра?
- параллелепипеда?

M, N, P
п.14, № 80