Вычисление объёмов геометрических тел с помощью определённого интеграла

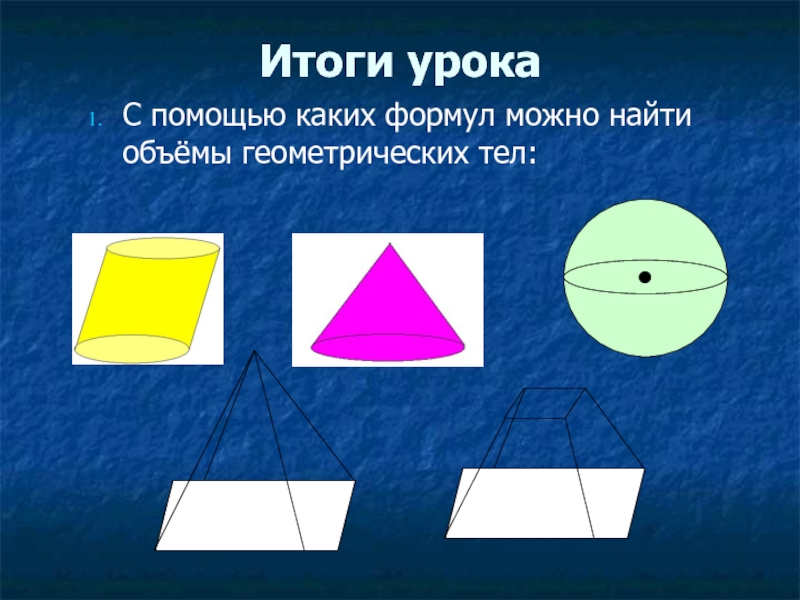
богатыре князе Гвидоне Салтановиче и о прекрасной царевне Лебеде»
И привез

гонец хмельной
В тот же день приказ такой:
«Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод».
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.

её основания 30 см, максимальная ширина – 80 см, а

высота бочки - 1 метр?

точки х=а и х=b, то разность значений F(b)-F(a) (где F(x)

- первообразная f(x) на I) называется определенным интегралом от функции f(x) от a до b.

формула Ньютона-Лейбница.

Вводим систему координат так, что ось ОХ перпендикулярна плоскостям.
3.

Проводим плоскость Ф(х) параллельно плоскостям через точку с абсциссой х.
4. Определяем вид сечения и выражаем площадь через функцию S(х).
5. Проверяем, является ли функция S(х) непрерывной на [a;b].

= х0, х1, х2, …хn=b
и проводим через хi плоскости перпендикулярно

ОХ.
7. Плоскости разбивают тело Т на n- тел Т1, Т2, Т3,... Тn с основаниями Ф(хi) и высотой Δxi= (b - a)/n

8. V≈Vn= (S(x1) + S(x2) +…+ S(xn) )Δxi= =(S(x1) + S(x2) +…+ S(xn))(b - a)/n. При n →∞, Vn→V, поэтому
но 9.

высотой h.
1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС)∩OX=a, a=0,

(A1B1C1) ∩ OX=b, b=h

3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.

Ответ: V=Sh

4. S(x) непрерывна на [0;h]

систему координат так, что ось ОХ перпендикулярна

основанию геометрического тела.
2. Найти пределы интегрирования а и b.
3. Провести сечение плоскостью перпендикулярно оси ОХ через точку с абсциссой х.
Определить вид сечения, задать формулой его площадь как функцию S(X).
4. Проверить непрерывность функции S(X) на [a;b].
5.

4
Группа № 5
Группа № 6

равна 100мм. Найдите длину радиуса основания цилиндра.
Стаканчик для мороженного конической

формы имеет 12см глубину и 5см по диаметру верхней части. На него сверху положили две ложки мороженного в виде полушарий диаметра 5см. Переполнит ли мороженное стаканчик если позволить ему растаять.
Инженер, рост которого 180см пришел рассмотреть новую сферическую цистерну для хранения воды. Он забрался в пустую цистерну, и, когда он поднялся на место, находящееся в 5м 40см над точкой, в которой цистерна упирается на землю, его голова коснулась верхнего края цистерны. Зная, что город потребляет в час 40тысяч литров воды, он немедленно рассчитал, на сколько часов может хватить полной цистерны. Как он это сделал и как он получил результат.
На полке в магазине стоят две банки земляничного варенья одного и того же сорта. Одна банка в 2 раза выше другой, но зато её диаметр в 2 раза меньше. Высокая банка стоит 23 цента, а низкая 43 цента. Какую купить выгоднее?
Основание прямого кругового конуса имеет диаметр 12 см, а высота конуса равна 12см. Конус наполнили водой, затем в конус опустили шар так, что он оперся на стенки конуса. над водой при этом оказалось ровно половина шара. Сколько воды осталось в конусе после того, как шар был вынут?

её основания 30 см, максимальная ширина – 80 см, а

высота бочки - 1 метр?