Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники вокруг нас 10-11 классы (интегрированный урок)
Содержание
- 1. Многогранники вокруг нас 10-11 классы (интегрированный урок)
- 2. « Правильных многогранников вызывающе мало
- 3. Цели урока :Систематизировать знания об основных видах
- 4. I. Многогранники в математике:Многогранник называется
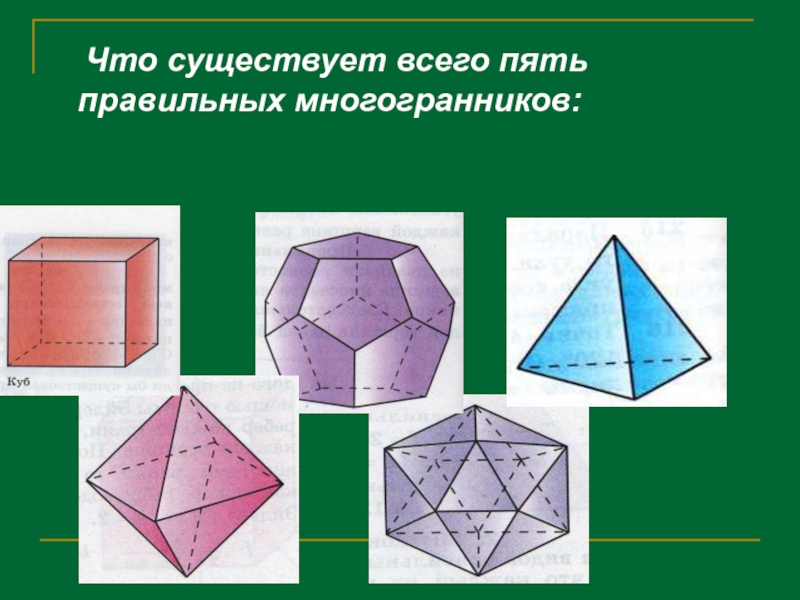
- 5. Что существует всего пять правильных многогранников:
- 6. Правильный октаэдр:Составлен из восьми равносторонних треугольников.
- 7. Правильный додекаэдр: Составлен из двенадцати правильных
- 8. Правильный икосаэдр:Составлен из двенадцати равносторонних треугольников. Каждая
- 9. Куб:Составлен из шести квадратов. Каждая
- 10. Правильный тетраэдр: Составлен из четырёх равносторонних треугольников.
- 11. Элементы симметрии додекаэдра:имеет центр симметрии – центрдодекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
- 12. Слайд 12
- 13. Доказано, что не существует правильного
- 14. Существует ли связь между числом вершин (В), граней (Г), ребер (Р) многогранника?
- 15. Теорема Эйлера: Для всякого выпуклого
- 16. II. Многогранники в истории.
- 17. Интерес к многогранникам человек проявляет на
- 18. Пять правильных тел
- 19. Додекаэдр - вселенная
- 20. Тетраэдр - огонь
- 21. Октаэдр – воздух.
- 22. Куб – земля.
- 23. Икосаэдр - вода
- 24. Пифагорейцы считали , что огонь
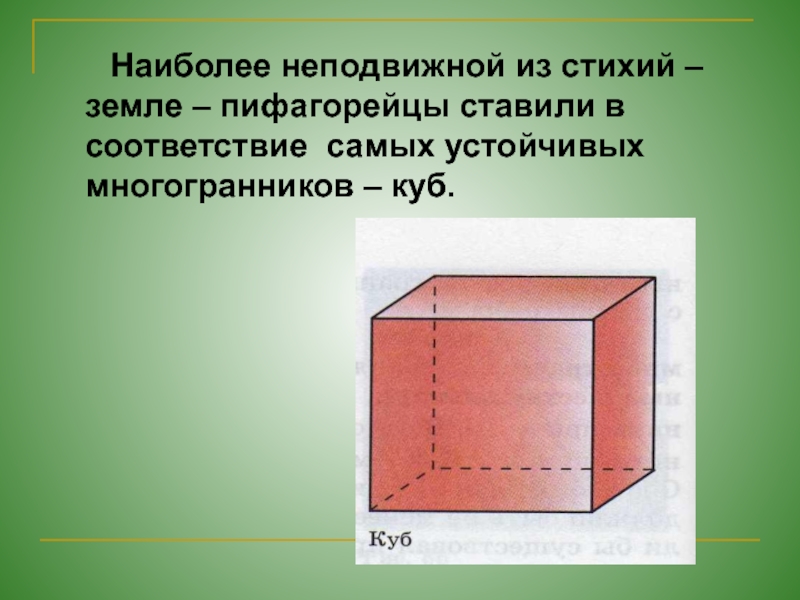
- 25. Наиболее неподвижной из стихий
- 26. III. Многогранники в биологии.
- 27. Математики говорили, что пчелы строили свои шестиугольные соты задолго до появления человека
- 28. Из правильных многоугольников с одинаковой
- 29. Пчелы – удивительные создания . Если
- 30. Одноклеточные организмы - Феодарии имеют форму
- 31. С помощью простых и сложных
- 32. Ученые считают , что ядро
- 33. Создания природы красивы и симметричны .Это неотделимое свойство природной гармонии.
- 34. Именно икосаэдр оказался в центре внимания
- 35. МНОГОГРАННИКИ В ИССКУСТВЕ, АРХИТЕКТУРЕ, ЖИВОПИСИ
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Работу выполнила ученица 10 класса Воронина Алина Учитель: Гаспарян И.В.
- 42. СПАСИБО ЗА ВНИМАНИЕ
- 43. Скачать презентанцию
« Правильных многогранников вызывающе мало , но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Слайды и текст этой презентации
Слайд 3Цели урока :
Систематизировать знания об основных видах многогранников, показать их
применения в других видах деятельности.
Развивать эвристическое мышление, показать, какую роль
играет математика в развитии общества.Развивать самостоятельность, творчество, морально-эстетические качества личности.
Слайд 4 I. Многогранники в математике:
Многогранник называется правильным, если все
его грани – равные правильные многоугольники и в каждой вершине
сходится одно и тоже число ребер.
Слайд 6 Правильный октаэдр:
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра
является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой
вершине равна 240 градусов.
Слайд 7Правильный додекаэдр:
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра
является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при
каждой вершине равна 324 градуса.
Слайд 8Правильный икосаэдр:
Составлен из двенадцати равносторонних треугольников. Каждая вершина является вершиной
пяти треугольников. Следовательно, сумма плоский углов при каждой вершине 300
градусов.
Слайд 9 Куб:
Составлен из шести квадратов. Каждая вершина куба является
вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине
равна 270 градусов.
Слайд 10Правильный тетраэдр:
Составлен из четырёх равносторонних треугольников. Каждая его вершина является
вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине
равна 180 градусов.
Слайд 11Элементы симметрии додекаэдра:
имеет центр симметрии – центр
додекаэдра, 15 осей симметрии
и
15 плоскостей симметрии.
Слайд 13 Доказано, что не существует
правильного многогранника, гранями
которого
являются правильные
шестиугольники. семиугольники и .т. д.
Слайд 15Теорема Эйлера:
Для всякого выпуклого многогранника между числами В,
Г, и Р выполняется соотношение:
В + Г - Р = 2
Слайд 17 Интерес к многогранникам человек
проявляет на протяжении всей своей
жизни – и малым ребёнком, играющим
деревянными кубиками, и зрелым
математиком.
Слайд 18 Пять правильных тел изучали Театет, Платон,
Евклид, Гипсилк, Папп.
Платон связал с
этими телами формы атомов основныхстихий природы.
Слайд 24
Пифагорейцы считали , что огонь состоит из мельчайших
частиц , имеющих форму тетраэдра.
Тетраэдр обладает рациональной
конструкцией: высокой прочностью при малом весе.
Слайд 25 Наиболее неподвижной из стихий – земле –
пифагорейцы ставили в соответствие самых устойчивых многогранников – куб.
Слайд 27 Математики говорили, что пчелы строили свои шестиугольные соты задолго
до появления человека
Слайд 28 Из правильных многоугольников с одинаковой площадью наименьший периметр именно у
правильных шестиугольников. Стало быть, мудрые пчёлы экономят воск и время
для постройки сот.
Слайд 29 Пчелы – удивительные создания . Если разрезать пчелиные соты
плоскостью, то станет видно сеть равных друг другу правильных шестиугольников
Слайд 30 Одноклеточные организмы -
Феодарии имеют форму икосаэдра. Геометрические свойства
икосаэдра помогают морскому микроорганизму преодолевать давление водной толщины.
Слайд 31 С помощью простых и сложных
атомов Платон попытался
даже
отразить взаимоотношения между
стихиями:
1 вода =
2 воздух + 1 огонь
Слайд 32 Ученые считают , что ядро земли
имеет форму и свойства растущего
кристалла , оказывавшего воздействие
на развитие всех природных процессов.
Слайд 34 Именно икосаэдр оказался в центре внимания биологов в их
спорах относительно формы вирусов. Геометрические свойства икосаэдра позволяют экономить генетическую
информацию.
