Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписанные и описанные окружности 8 класс
Содержание
- 1. Вписанные и описанные окружности 8 класс
- 2. Около окружности, радиус которой равен √8 ,
- 3. Найдите радиус окружности, описанной около прямоугольного треугольника
- 4. Найдите радиус окружности, вписанной в квадрат ABCD,
- 5. Найдите радиус окружности, описанной около правильного треугольника
- 6. Найдите радиус r окружности, вписанной в четырехугольник
- 7. В четырехугольник ABCD вписана окружность, АВ=10 ,
- 8. К окружности, вписанной в треугольник ABC, проведены
- 9. Боковые стороны равнобедренного треугольника равны 5, основание
- 10. Боковые стороны трапеции, описанной около окружности, равны
- 11. Периметр правильного шестиугольника равен 72. Найдите диаметр
- 12. Угол между стороной правильного n-угольника, вписанного в
- 13. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник,
- 14. Около трапеции описана окружность. Периметр трапеции равен
- 15. Боковая сторона равнобедренной трапеции равна ее меньшему
- 16. Два угла вписанного в окружность четырехугольника равны
- 17. Углы A ,B и C четырехугольника ABCD
- 18. Одна сторона треугольника равна радиусу описанной окружности.
- 19. Сторона AB треугольника ABC равна 1. Противолежащий
- 20. Сторона AB тупоугольного треугольника ABC равна радиусу
- 21. Три стороны описанного около окружности четырехугольника относятся
- 22. Найдите радиус R окружности, описанной около треугольника
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Задания В4 из Открытого банка заданий 2014
Вписанные и описанные
окружности
Презентация выполнена
учителем математики Дорошенко Н.И.
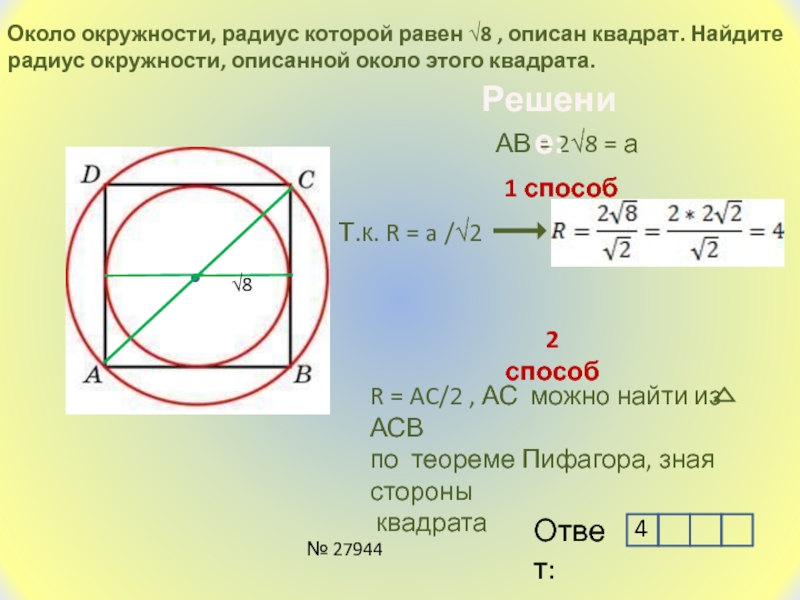
Слайд 2Около окружности, радиус которой равен √8 , описан квадрат. Найдите
радиус окружности, описанной около этого квадрата.
√8
АВ = 2√8 =
а Т.к. R = a /√2
1 способ
2 способ
R = AC/2 , АС можно найти из АСВ
по теореме Пифагора, зная стороны
квадрата
4
Решение:
№ 27944
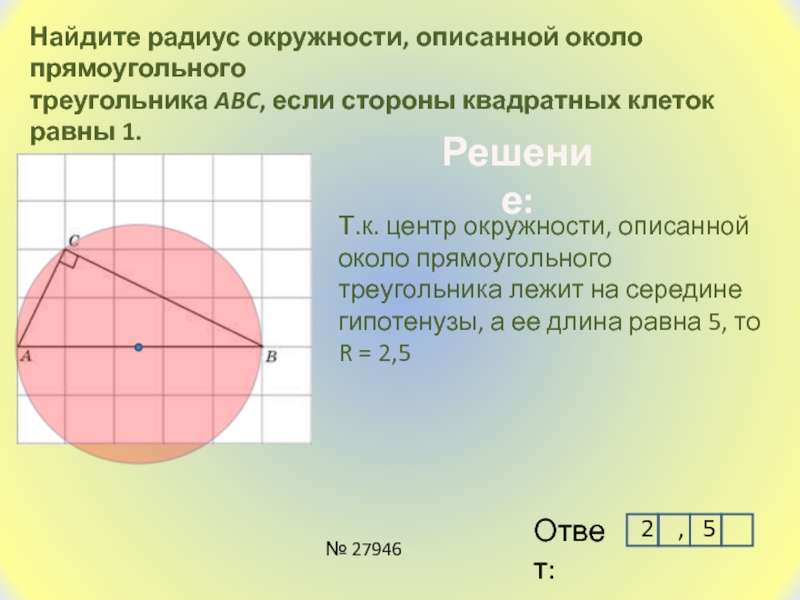
Слайд 3Найдите радиус окружности, описанной около прямоугольного
треугольника ABC, если стороны
квадратных клеток равны 1.
Т.к. центр окружности, описанной около прямоугольного
треугольника лежит на середине гипотенузы, а ее длина равна 5, то R = 2,52 , 5
Решение:
№ 27946
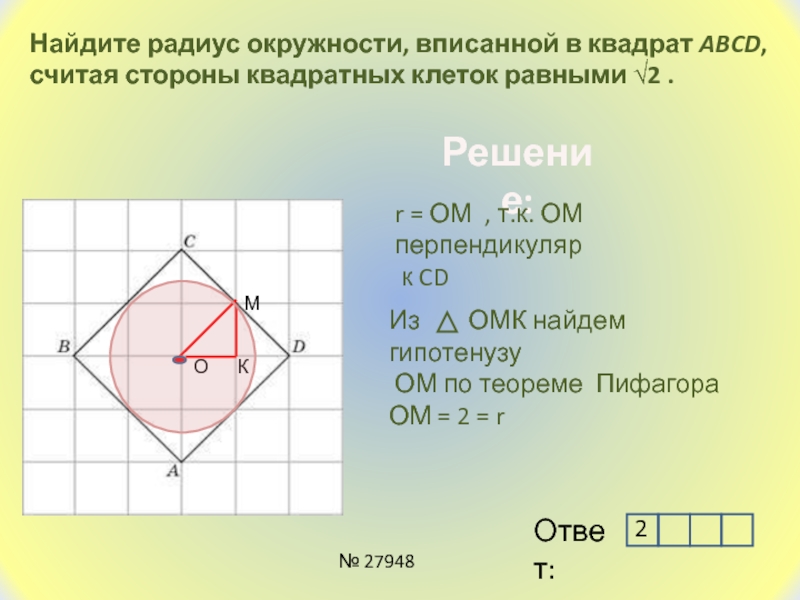
Слайд 4Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных
клеток равными √2 .
Решение:
r = ОМ , т.к. ОМ перпендикуляр
к CDО
М
К
Из ОМК найдем гипотенузу
ОМ по теореме Пифагора
ОМ = 2 = r
2
№ 27948
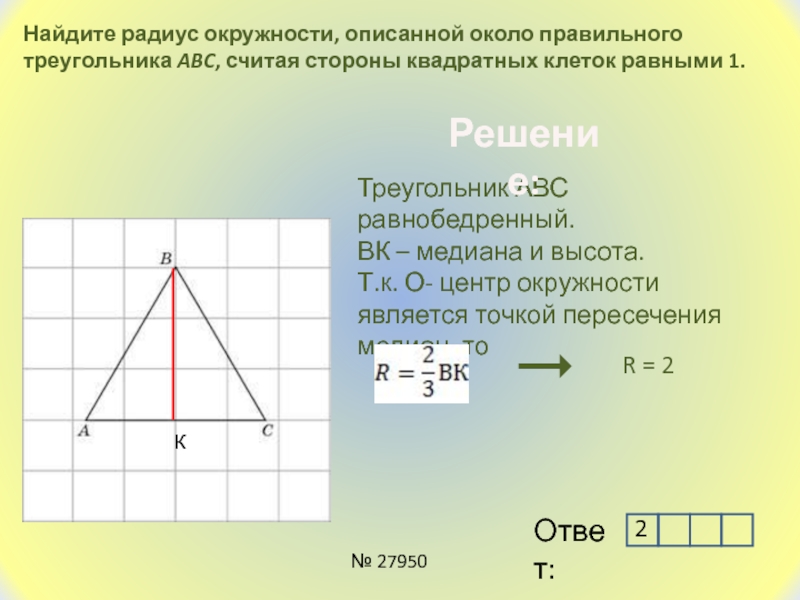
Слайд 5Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны
квадратных клеток равными 1.
К
Треугольник АВС равнобедренный.
ВК – медиана и
высота.Т.к. О- центр окружности является точкой пересечения медиан, то
R = 2
2
Решение:
№ 27950
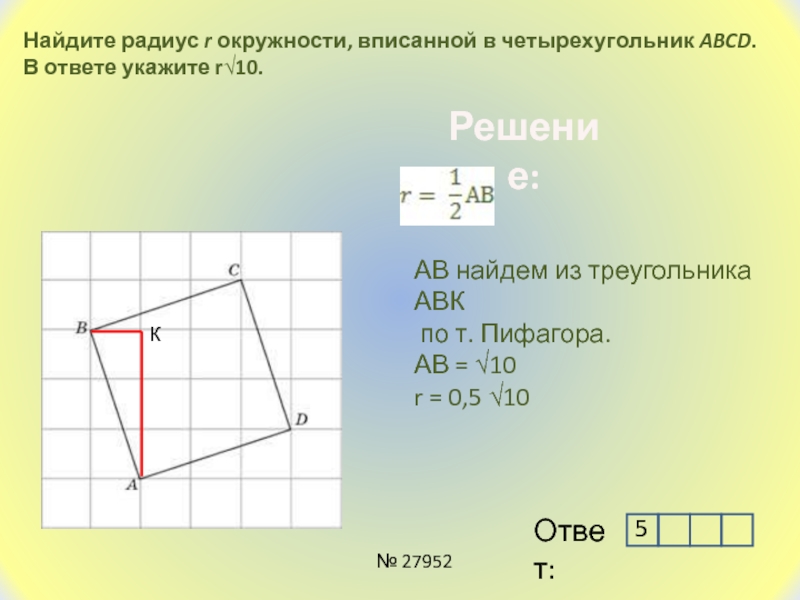
Слайд 6Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе
укажите r√10.
АВ найдем из треугольника АВК
по т. Пифагора.
АВ
= √10r = 0,5 √10
К
5
Решение:
№ 27952
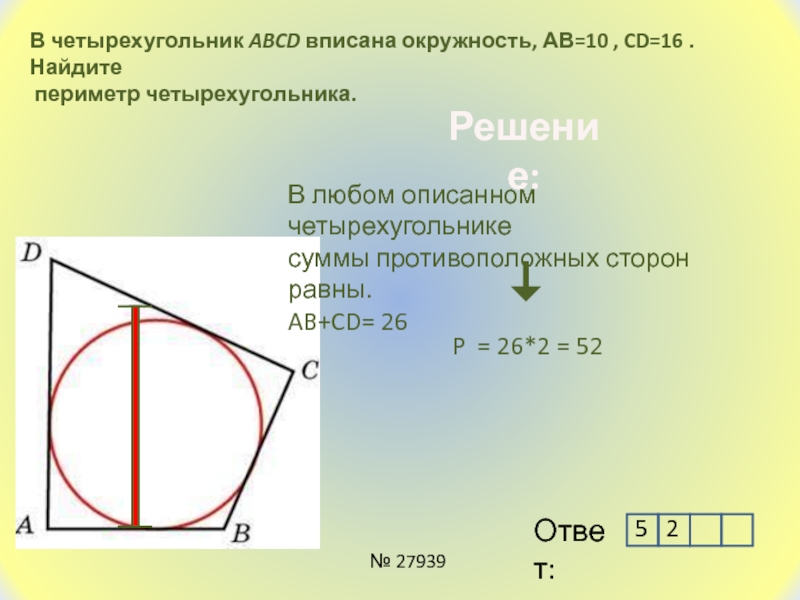
Слайд 7В четырехугольник ABCD вписана окружность, АВ=10 , CD=16 . Найдите
периметр четырехугольника.
Решение:
В любом описанном четырехугольнике
суммы противоположных сторон равны.
AB+CD= 26
P =
26*2 = 525 2
№ 27939
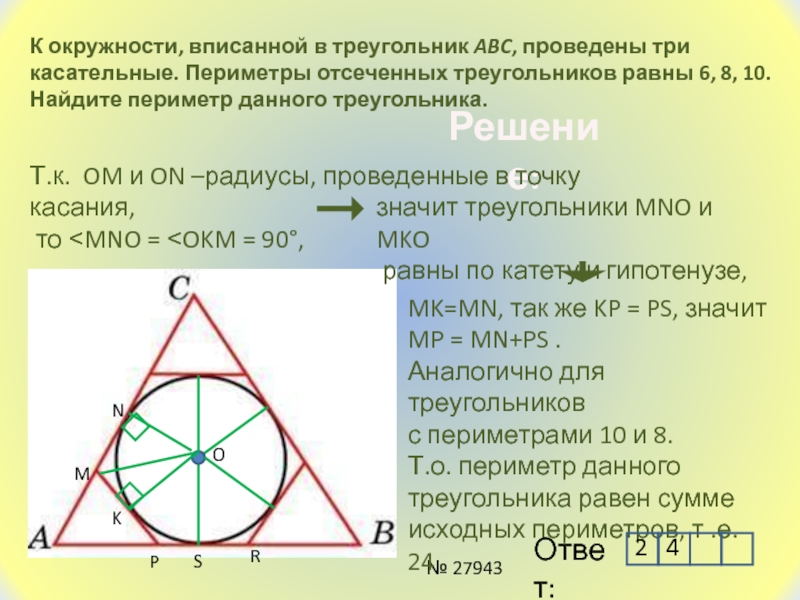
Слайд 8К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры
отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
№
27943Решение:
M
N
O
K
Т.к. OM и ON –радиусы, проведенные в точку касания,
то ˂MNO = ˂OKM = 90°,
значит треугольники MNO и MKO
равны по катету и гипотенузе,
MK=MN, так же KP = PS, значит
MP = MN+PS .
Аналогично для треугольников
с периметрами 10 и 8.
Т.о. периметр данного
треугольника равен сумме
исходных периметров, т .е. 24
P
R
S
2 4
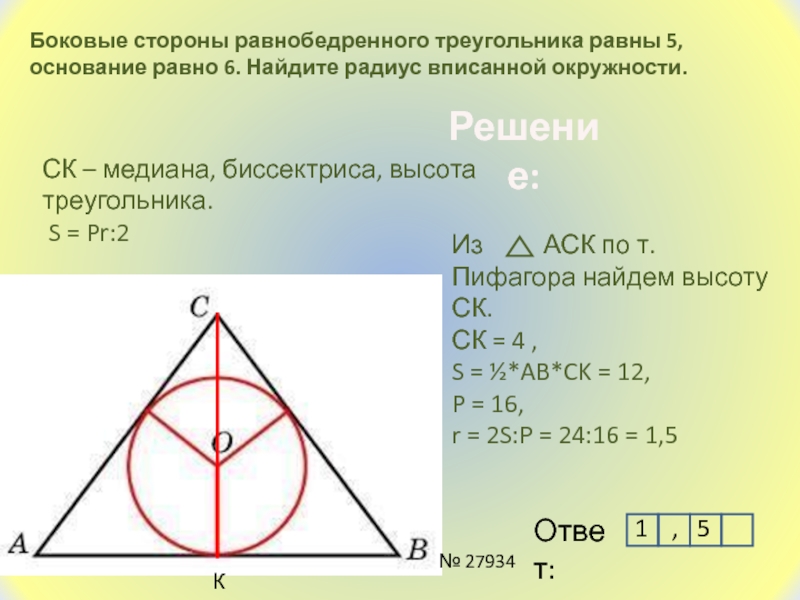
Слайд 9Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите
радиус вписанной окружности.
К
Решение:
СК – медиана, биссектриса, высота
треугольника.
Из
АСК по т.Пифагора найдем высоту СК.СК = 4 ,
S = ½*AB*CK = 12,
P = 16,
r = 2S:P = 24:16 = 1,5
№ 27934
1 , 5
S = Pr:2
Слайд 10Боковые стороны трапеции, описанной около окружности, равны 3 и 5.
Найдите среднюю линию трапеции.
Решение:
В любом описанном четырехугольнике суммы противоположных
сторон равны.DC+AB = 8
Таким образом MN = 4
M
N
Пусть MN – средняя линия трапеции,
МN = ½(DC+AB)
АD+CB = 8
4
№ 27936
Слайд 11Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
Решение:
P =
72 , значит a = 12 , т.к. R =
a = 12D = 2R = 24
2 4
№ 27929
Слайд 12Угол между стороной правильного n-угольника, вписанного в окружность,
и радиусом
этой окружности, проведенным в одну из вершин стороны,
равен 54°
. Найдите n.№ 27930
54
Решение:
А
В
С
˂ А = 180° - 54°*2 = 72°
АВ = АС = R
ABC равнобедренный
n = 360° : 72° = 5
5
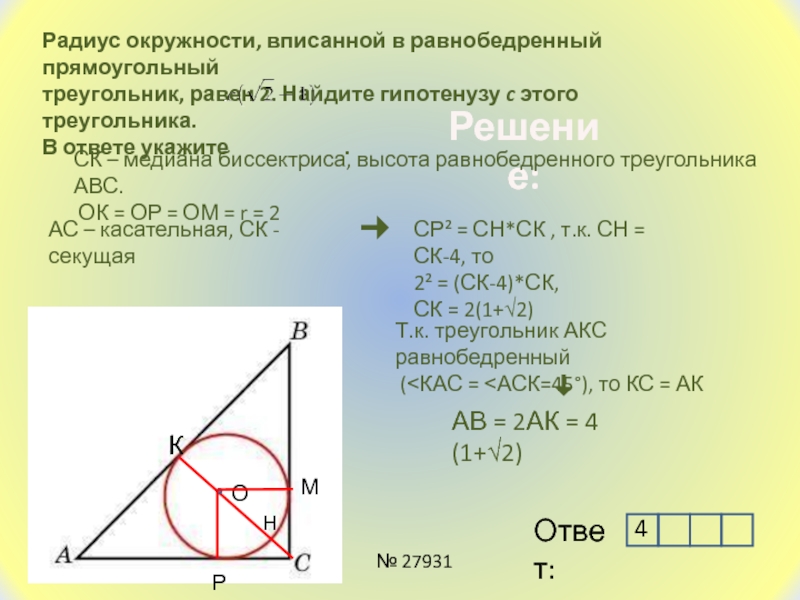
Слайд 13Радиус окружности, вписанной в равнобедренный прямоугольный
треугольник, равен 2. Найдите
гипотенузу c этого треугольника.
В ответе укажите
.К
Решение:
№ 27931
СК – медиана биссектриса, высота равнобедренного треугольника АВС.
ОК = ОР = ОМ = r = 2
О
М
Р
АС – касательная, СК - секущая
СР² = СН*СК , т.к. СН = СК-4, то
2² = (СК-4)*СК,
СК = 2(1+√2)
Н
Т.к. треугольник АКС равнобедренный
(˂КАС = ˂АСК=45°), то КС = АК
АВ = 2АК = 4 (1+√2)
4
Слайд 14Около трапеции описана окружность. Периметр трапеции равен 22,
средняя линия
равна 5. Найдите боковую сторону трапеции.
№ 27924
Решение:
Т.к.
, то DC+AB = 10AD + CB = P – 10 = 12
Т.к. в любом вписанном четырехугольнике сумма противоположных углов равна 180° , то
ABCD – равнобедренная трапеция.
AD = 6
6
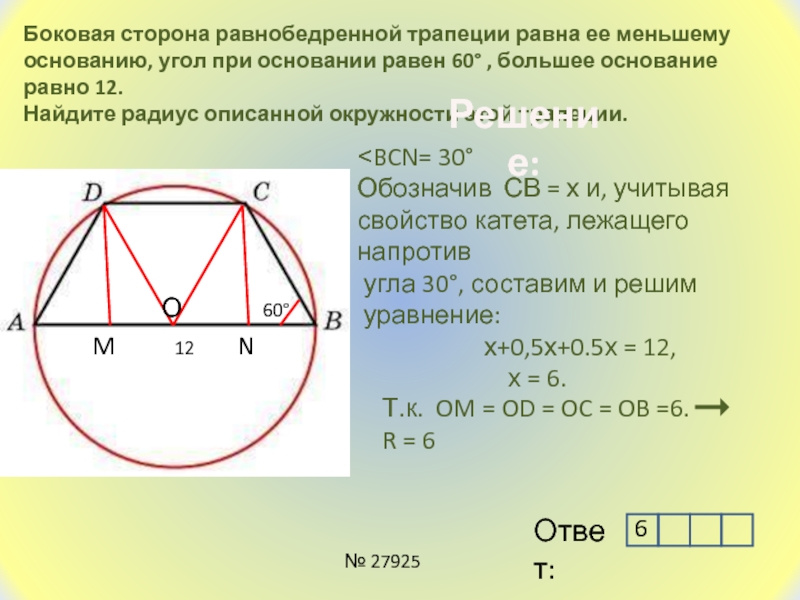
Слайд 15Боковая сторона равнобедренной трапеции равна ее меньшему
основанию, угол при
основании равен 60° , большее основание равно 12.
Найдите радиус
описанной окружности этой трапеции. 60°
12
M
N
№ 27925
Решение:
˂BCN= 30°
Обозначив СВ = х и, учитывая
свойство катета, лежащего напротив
угла 30°, составим и решим
уравнение:
х+0,5х+0.5х = 12,
х = 6.
О
Т.к. OM = OD = OC = OB =6.
R = 6
6
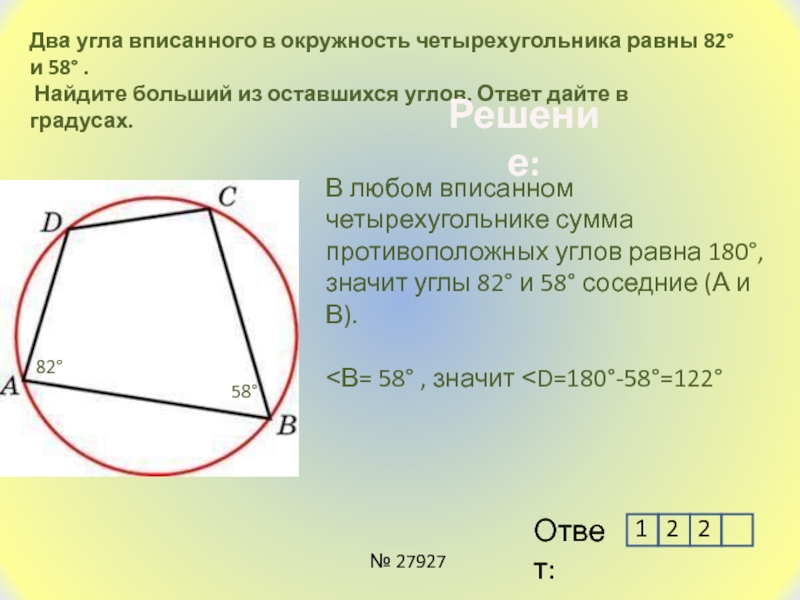
Слайд 16Два угла вписанного в окружность четырехугольника равны 82° и 58°
.
Найдите больший из оставшихся углов. Ответ дайте в градусах.
№
27927В любом вписанном четырехугольнике сумма противоположных углов равна 180°, значит углы 82° и 58° соседние (А и В).
˂В= 58° , значит ˂D=180°-58°=122°
Решение:
1 2 2
82°
58°
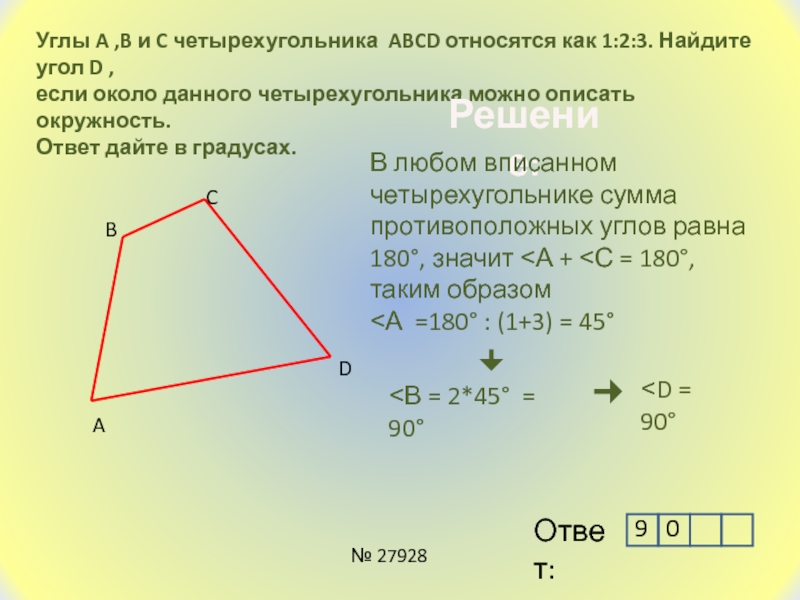
Слайд 17Углы A ,B и C четырехугольника ABCD относятся как 1:2:3.
Найдите угол D ,
если около данного четырехугольника можно описать
окружность. Ответ дайте в градусах.
№ 27928
Решение:
A
B
C
D
В любом вписанном четырехугольнике сумма противоположных углов равна 180°, значит ˂А + ˂С = 180°, таким образом
˂А =180° : (1+3) = 45°
˂В = 2*45° = 90°
˂D = 90°
9 0
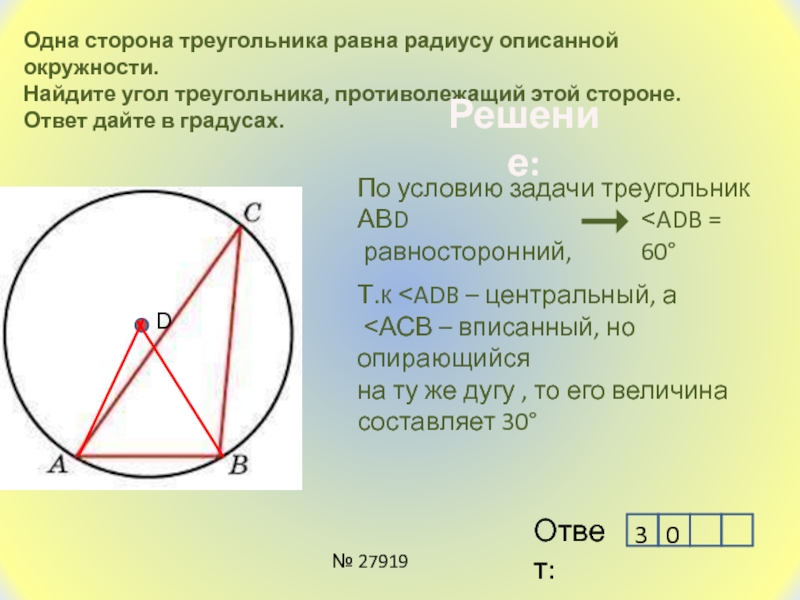
Слайд 18Одна сторона треугольника равна радиусу описанной окружности.
Найдите угол треугольника,
противолежащий этой стороне.
Ответ дайте в градусах.
№ 27919
Решение:
D
По условию задачи
треугольник АВDравносторонний,
Т.к ˂ADB – центральный, а
˂АСВ – вписанный, но опирающийся
на ту же дугу , то его величина
составляет 30°
3 0
˂ADB = 60°
Слайд 19Сторона AB треугольника ABC равна 1. Противолежащий ей угол C
равен150° .
Найдите радиус окружности, описанной около этого треугольника.
№ 27921
Решение:
О
˂ACB
– вписанный, значит дуга на которую он опирается равна 300°
Величина дуги АСВ, а значит и
центрального ˂АОВ = 60° , а т.к.
АО = ОВ = R, то треугольник АОВ
равносторонний,
R = 1`
1
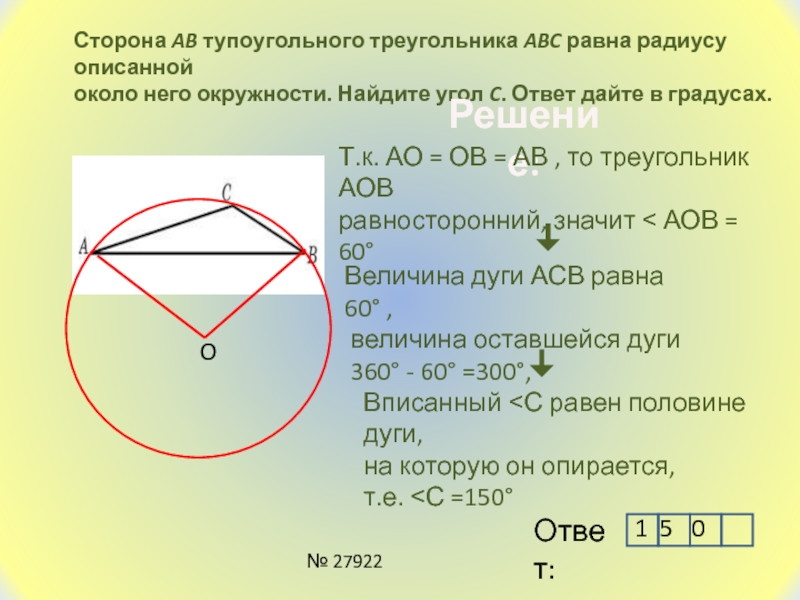
Слайд 20Сторона AB тупоугольного треугольника ABC равна радиусу описанной
около него
окружности. Найдите угол C. Ответ дайте в градусах.
№ 27922
Решение:
O
Т.к. АО
= ОВ = АВ , то треугольник АОВ равносторонний, значит ˂ АОВ = 60°
Величина дуги АСВ равна 60° ,
величина оставшейся дуги
360° - 60° =300°,
Вписанный ˂С равен половине дуги,
на которую он опирается,
т.е. ˂С =150°
1 5 0
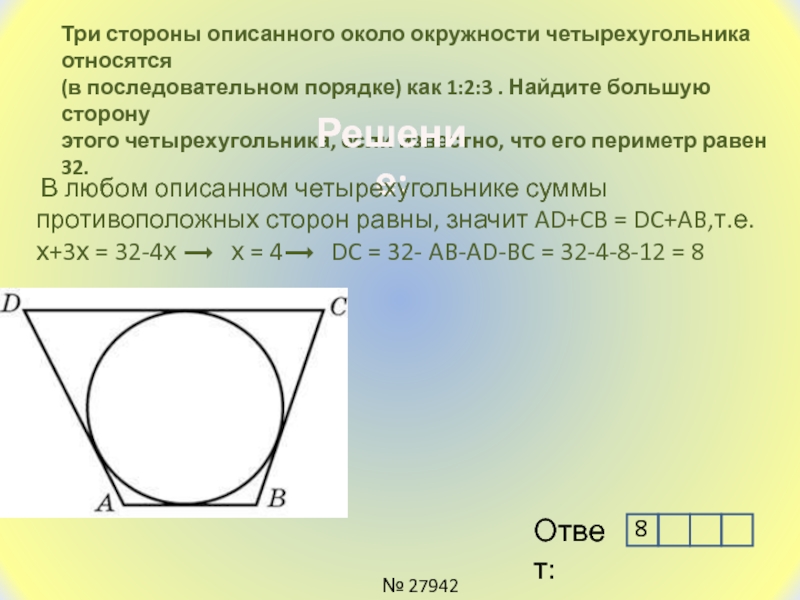
Слайд 21Три стороны описанного около окружности четырехугольника относятся
(в последовательном порядке)
как 1:2:3 . Найдите большую сторону
этого четырехугольника, если известно,
что его периметр равен 32.Решение:
№ 27942
В любом описанном четырехугольнике суммы противоположных сторон равны, значит AD+CB = DC+AB,т.е.
х+3х = 32-4х х = 4 DC = 32- AB-AD-BC = 32-4-8-12 = 8
8
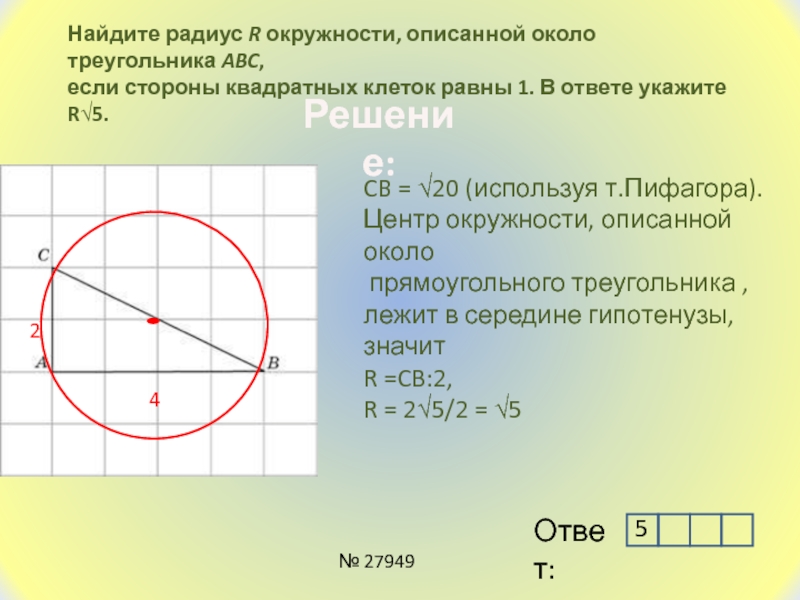
Слайд 22Найдите радиус R окружности, описанной около треугольника ABC,
если стороны
квадратных клеток равны 1. В ответе укажите R√5.
Решение:
4
2
CB = √20
(используя т.Пифагора).Центр окружности, описанной около
прямоугольного треугольника ,
лежит в середине гипотенузы, значит
R =CB:2,
R = 2√5/2 = √5
5
№ 27949