Повторение планиметрии

двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в

пределах одной плоскости. Фигуры, изучаемые планиметрией:

Точка
Прямая
Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб)
Трапеция
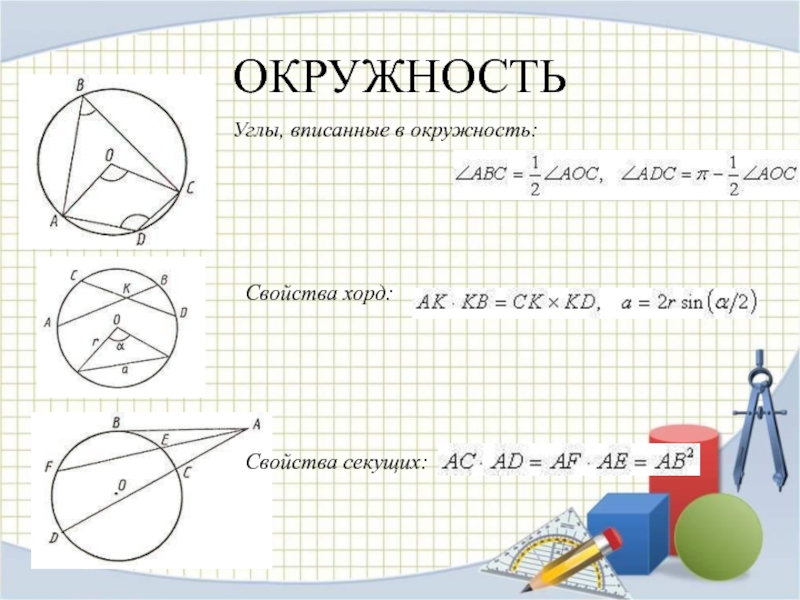
Окружность
Треугольник
Многоугольник

но не имеющий размеров, массы, направленности и каких-либо других геометрических

или физических характеристик. Одно из фундаментальных понятий в математике и физике.

Прямая. Прямая линия — одно из основных понятий геометрии. При систематической изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной

прямой, и тремя отрезками, попарно соединяющими эти точки.

треугольника:
Площадь прямоугольного треугольника
Площадь
равностороннего треугольника

— линия) — это четырехугольник, у которого противолежащие стороны попарно

параллельны, т. е. лежат на параллельных прямых. Частным случаем параллелограмма (являются прямоугольник и ромб.

пересечения делятся пополам.
Формула площади параллелограмма:
Формула периметра параллелограмма:

две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции.

Две другие стороны называются боковыми сторонами . Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

С

D

А

В

одинаково удалены от данной точки (центра окружности), лежащей в той

же плоскости, что и кривая.

:
Площадь круга:

Площадь сектора в

радиан:

Площадь сектора в :

Площадь кругового сегмента,
содержащего дугу в :

замкнутая ломаная без самопересечений, однако иногда самопересечения допускаются. Иногда многоугольник

определяется как замкнутая область плоскости ограниченная замкнутой ломаной без самопересечений. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины
многоугольника, называются диагоналями.

– вершины многоугольника
 
 
Площадь правильного многоугольника (S) равна:

S= r·p=1/2r·n·a