Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стереометрия. Взаимное расположение прямых в пространстве. Угол между скрещивающимися прямыми 11 класс
Содержание
- 1. Стереометрия. Взаимное расположение прямых в пространстве. Угол между скрещивающимися прямыми 11 класс
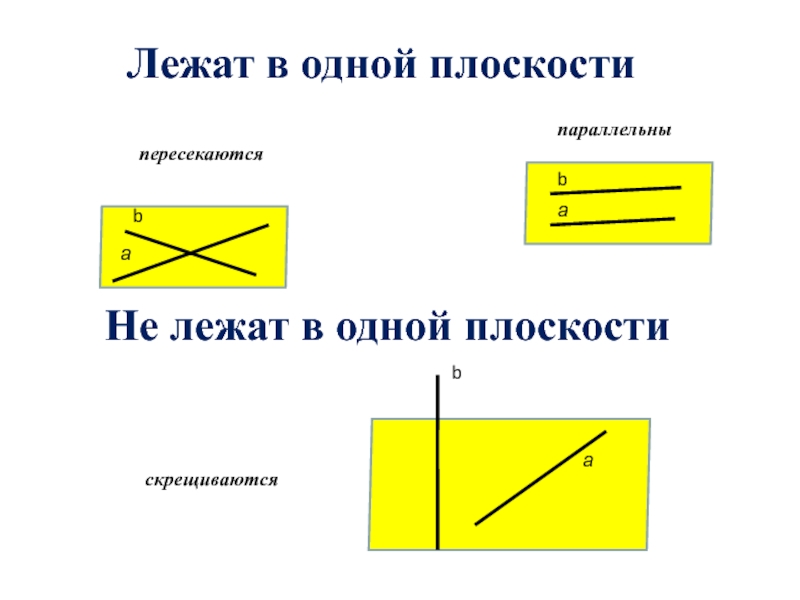
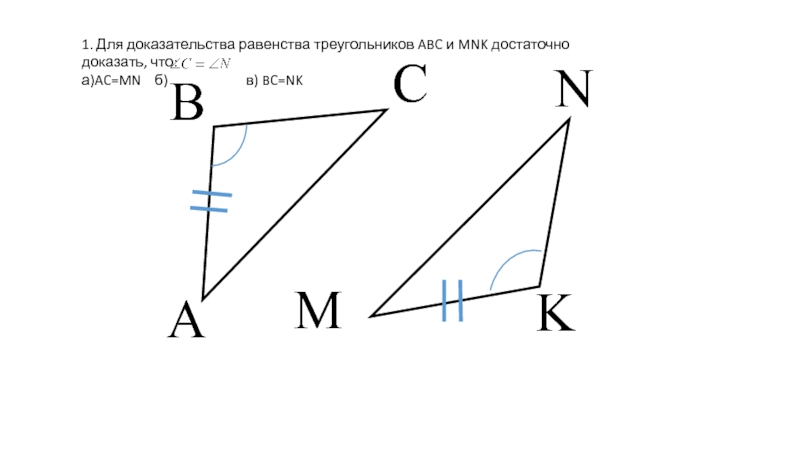
- 2. пересекаютсяпараллельныааbbскрещиваютсяаbНе лежат в одной плоскостиЛежат в одной плоскости
- 3. Угол между пересекающимися прямыми
- 4. Угол между скрещивающимися прямымиаb
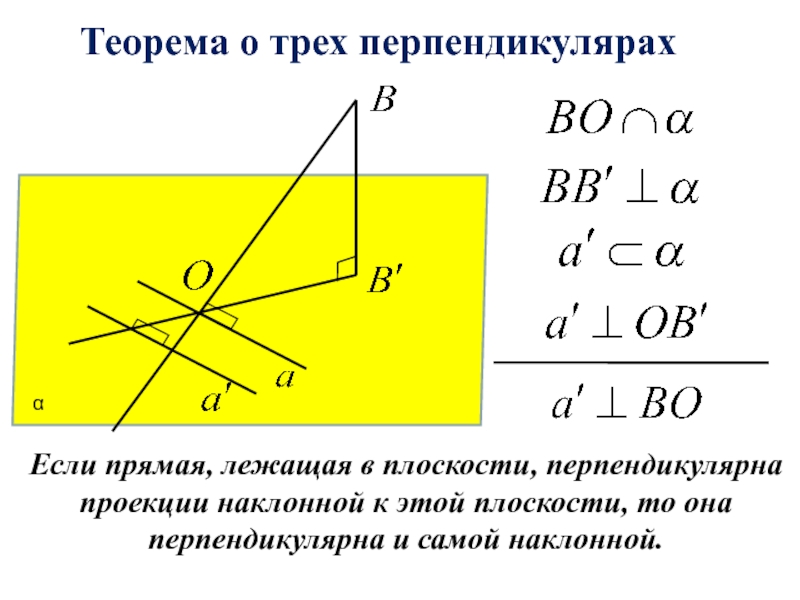
- 5. Перпендикулярные прямые в пространстве
- 6. Теорема о трех перпендикулярахαЕсли прямая, лежащая в
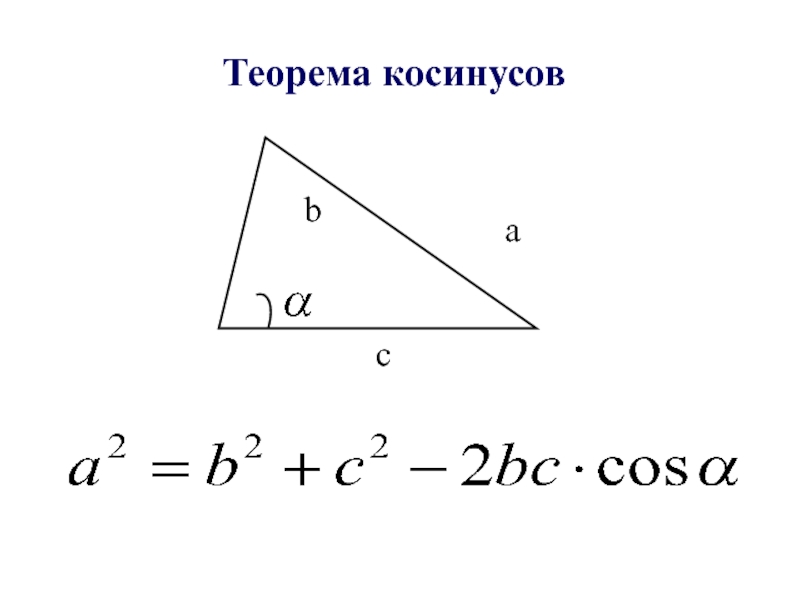
- 7. Теорема косинусов
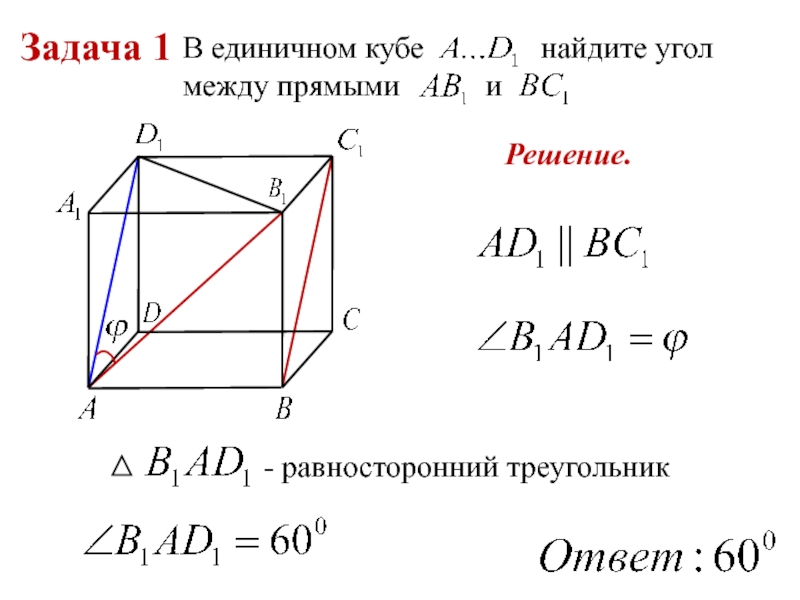
- 8. Задача 1В единичном кубе
- 9. Задача 2В единичном кубе
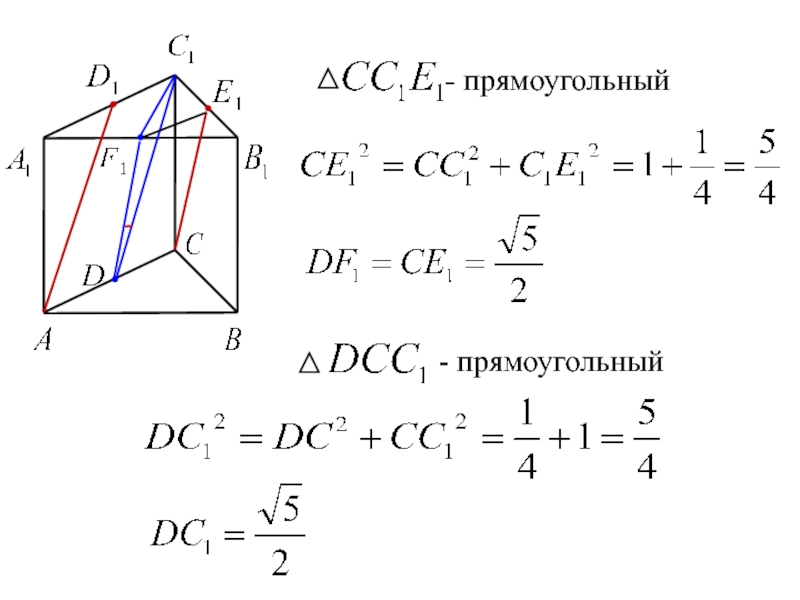
- 10. Задача 3В единичном кубе
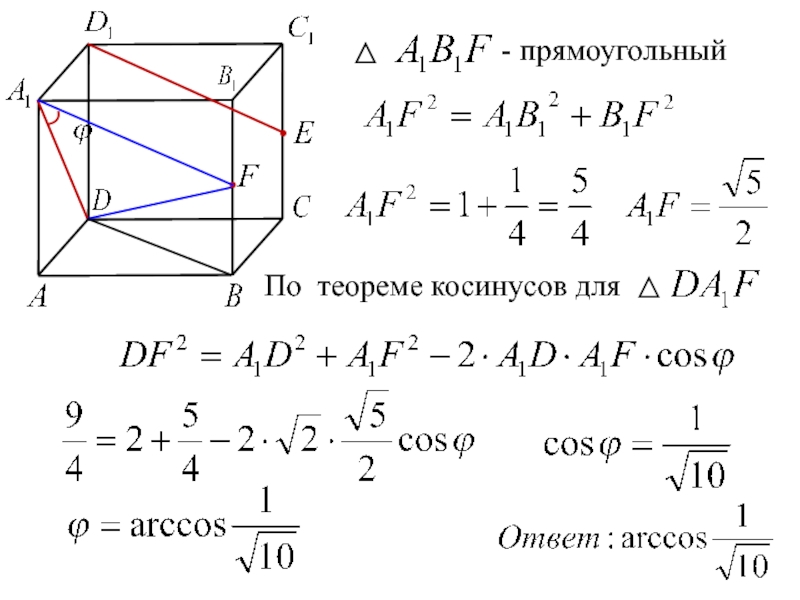
- 11. - прямоугольныйПо теореме косинусов для
- 12. Задача 4
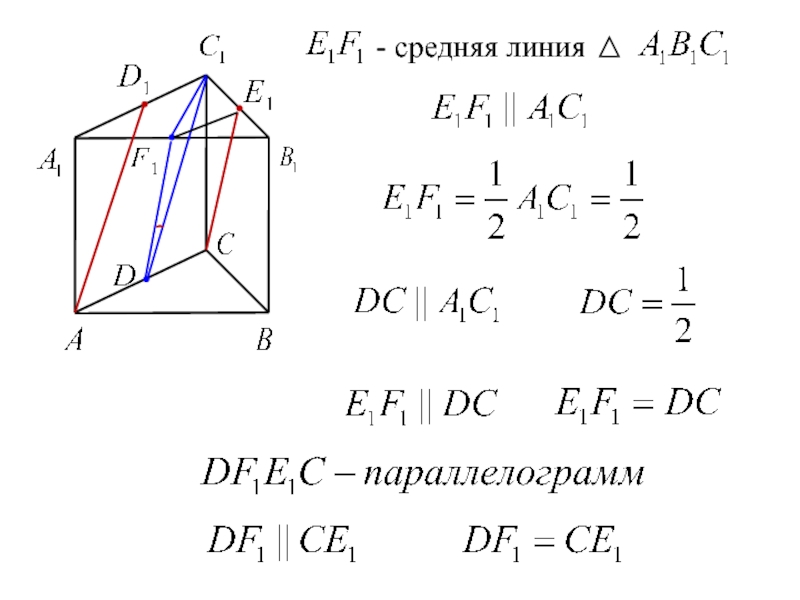
- 13. - средняя линия
- 14. - прямоугольный- прямоугольный
- 15. По теореме косинусов для - прямоугольный
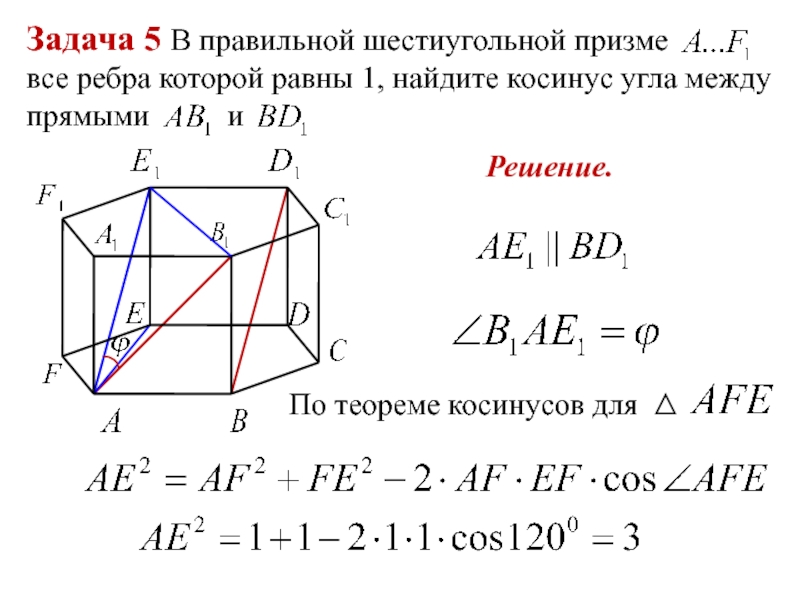
- 16. Задача 5 В правильной шестиугольной призме
- 17. - прямоугольныйПо теореме косинусов для
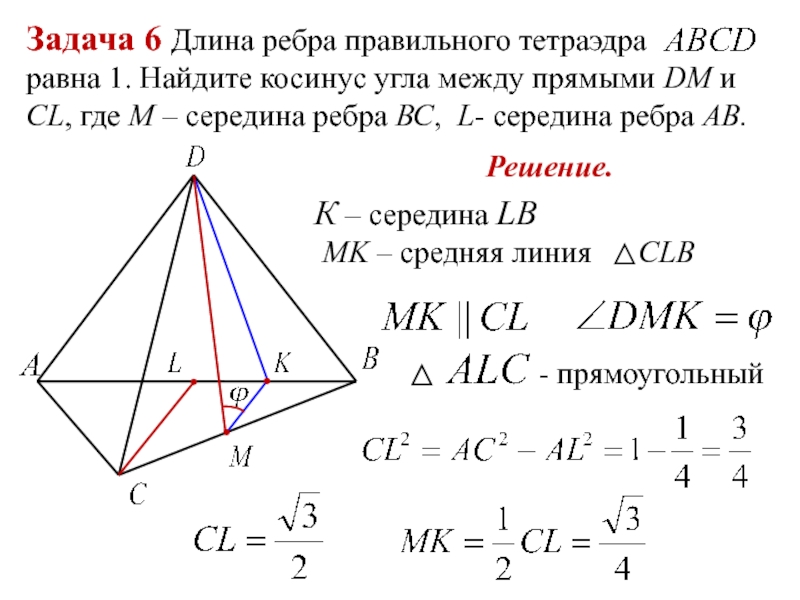
- 18. Задача 6 Длина ребра правильного тетраэдра
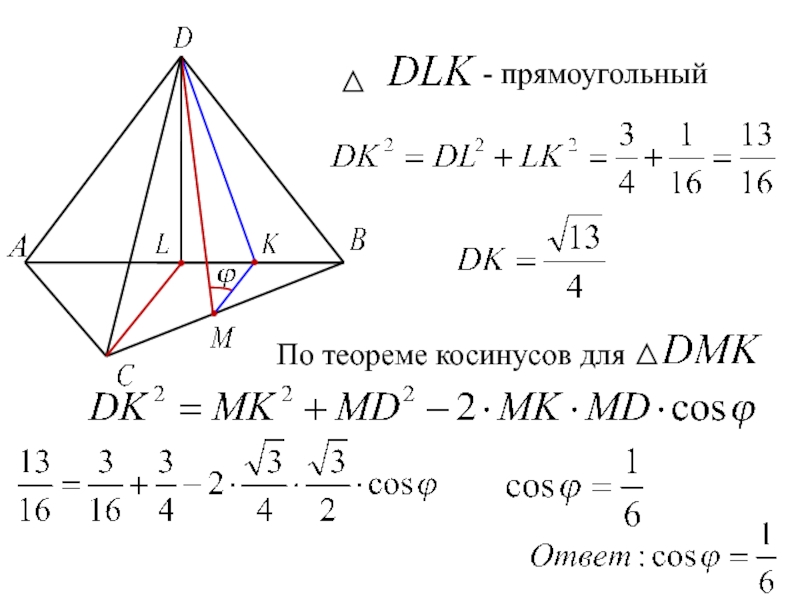
- 19. - прямоугольныйПо теореме косинусов для
- 20. Скачать презентанцию
пересекаютсяпараллельныааbbскрещиваютсяаbНе лежат в одной плоскостиЛежат в одной плоскости
Слайды и текст этой презентации
Слайд 6
Теорема о трех перпендикулярах
α
Если прямая, лежащая в плоскости, перпендикулярна проекции
наклонной к этой плоскости, то она перпендикулярна и самой наклонной.
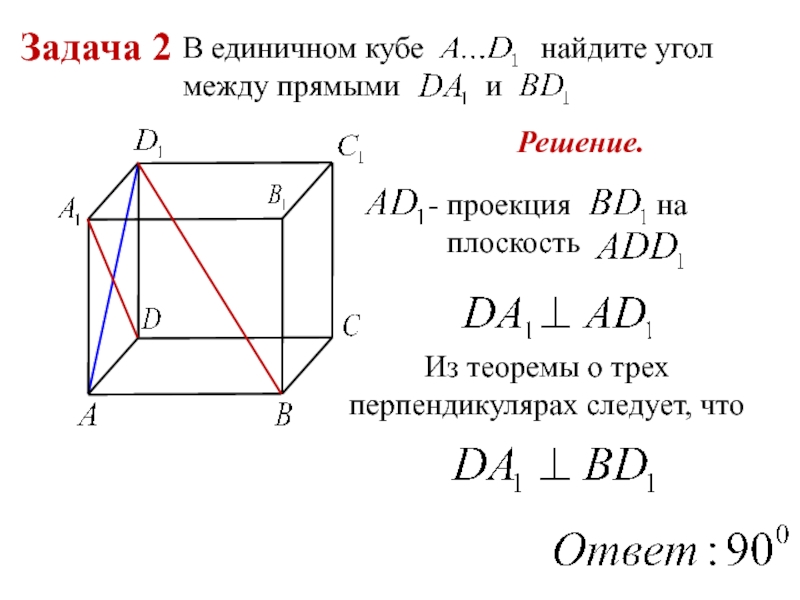
Слайд 9Задача 2
В единичном кубе
найдите угол между прямыми
и
проекция на
плоскость
Из теоремы о трех перпендикулярах следует, что
Решение.
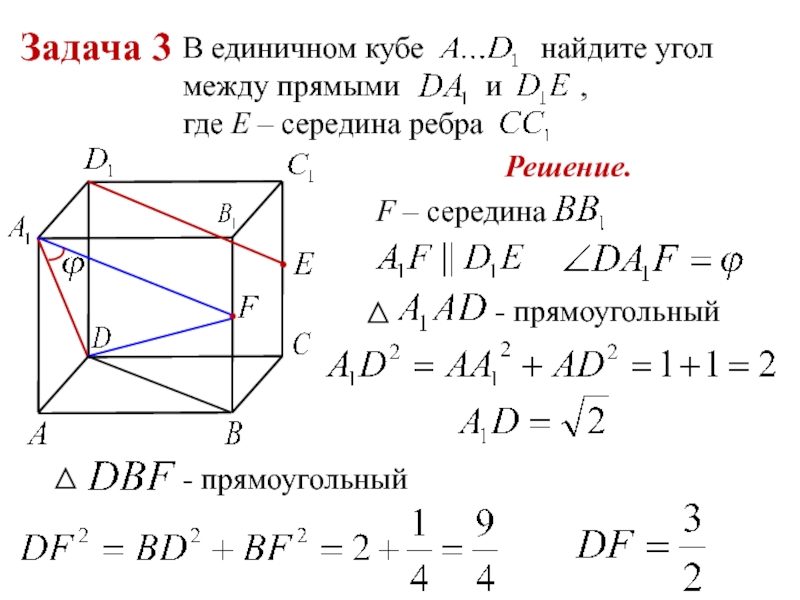
Слайд 10Задача 3
В единичном кубе
найдите угол между прямыми
и , где E – середина ребра
Решение.
F – середина
- прямоугольный
- прямоугольный
Слайд 12Задача 4
В правильной треугольной призме
все ребра которой равны 1, найдите косинус угла между прямыми и , где и - соответственно середины ребер и
Решение.
D – середина ребра АС
– середина ребра
Слайд 16Задача 5 В правильной шестиугольной призме
все ребра которой равны 1,
найдите косинус угла между прямыми и
Решение.
По теореме косинусов для
Слайд 18Задача 6 Длина ребра правильного тетраэдра
равна 1. Найдите косинус угла между прямыми DМ и CL,
где М – середина ребра ВС, L- середина ребра АВ.Решение.
К – середина LB
MK – средняя линия CLB
- прямоугольный
